先回は作用点の同じ力の釣合いについて説明しました。
まだ見ておられない方は下のリンクから見ることができます。
「あいつとこいつは釣合っている…?皆さん、力の話です。力の釣合いについて解説!」
今回は作用点が違う力の釣合いについてです。
ではまず、力の釣合いについて確認しましょう。
(先回と同じ内容ですので、すでに見た方は飛ばしても大丈夫です。)
力の釣合いとは?
まずは力のつり合いという言葉の意味を理解しましょう。
「釣合い」という言葉は日常生活でもよく耳にしますね。
例えば
「俺なんかあんな美人とは釣合わない…」
とか聞いたら意味を理解することはできると思います。
…なんか悲しい例えができてしまいましたが、簡単に言うと「釣合う」とは、バランスが取れている状態のことです。
つまり「力が釣合っている」とは力同士がバランスをとっている状態のことを指します。
力同士がバランスをとっているとはどういう状況でしょうか?
大勢で綱引きしているところを想像してみてください。

みんな頑張って引いていますが、相手も引いていて、綱の真ん中は動いていません。
これが、力が釣合っている状態です。
自分たちが引いている力と相手が引いている力がバランスをとっている、つまり力が釣合っています。
まとめると、力が釣合っている状態とは、複数の力が物にかかっているにもかかわらず、動いていない状態のことです。
建物の躯体(柱や梁など)はいろいろな力がかかっているにもかかわらず、ピクリとも動かず建物を支えています。
これは力が釣合っているからです。
身近に力の釣合いがある、と思うと少し親近感わきませんか?
では、今回の本題「作用点の違う力の釣合い」について解説していきたいと思います。
【作用点の違う力の釣合い】 解説
【作用点の違う力の釣合い】釣合い条件
…と言っても何か大きく変わることはありません。
一つだけ新しい釣合い条件が出てきます。
先ほど確認しましたが、釣合いとはそれぞれの力を合わせた時にバランスがとれていることです。
このバランスという中には、横に動かない、縦に動かないだけではなく、回らない、という意味があります。
つまり、新しい釣合い条件は
ΣM=0
です。
(ΣM=0とは物体に働くモーメント力の合計が0になるという意味です。
モーメントについては下の記事で詳しく解説しています。)
これは図式解法、算式解法ともに同じことがいえます。
例題をもとに確認していきましょう。
【作用点の違う力の釣合い】 例題
下の図のように力Pが働いたときA,Bにはそれぞれどのような力を働かせたら釣合うか求めなさい。
ただし、力Pの作用線とA,Bにかかる力は平行とします。
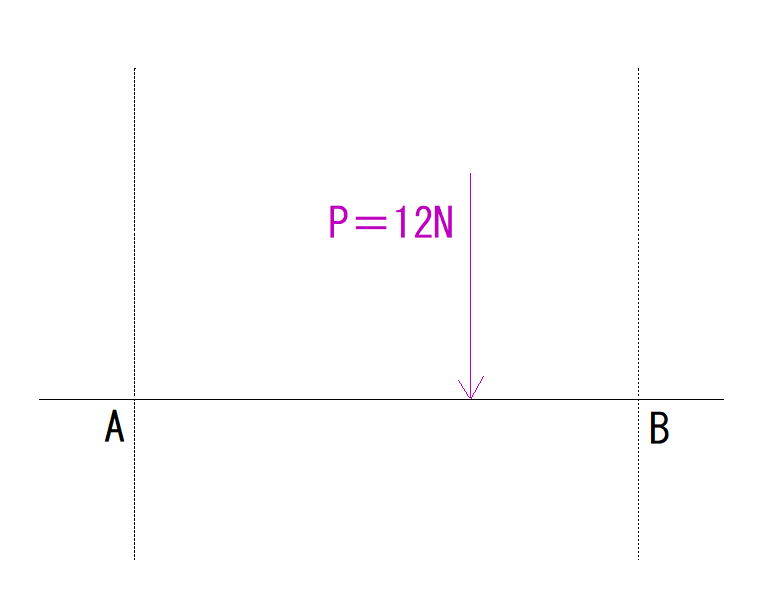
【作用点の違う力の釣合い】図式解法
「新しい分野で、よくわからない~」となっていませんか?
実はこれは、すでに習った分野を組み合わせることで解くことができます。
意外と簡単に解いていくことができる分野の問題なのです。
では早速考え方を理解していきましょう。
まず、力Pに釣合う、ということは、A,Bの合力がPと同じ位置で同じ大きさで、逆向きになっている必要があります。


…この図どこかで見たことありませんか?
そうです!
「力を平行に分解」の分野で学びました!
上のリンクからやり方を詳しく知ることができます。
つまり、この合力になるように分力を求めることで、釣合う力を求めることができます。
もう一度ここでもやり方を確認してみましょう。
【作用点の違う力の釣合い】図式解法 手順
(手順については「力を平行に分解…えっ意外と面倒くさい?図式解法 算式解法まとめて徹底解説!」の転載です。)
①Pを同じ大きさのまま解答欄の別のところに平行移動し示力図を書きます。
そして任意の場所に点O(極点といいます)を書きます。

②極点からPの両端a,bに線をひき(極線)、極線には番号を付けておきましょう。

③極線を問題文に合力のところで交わるように平行移動します。(連力図に書かれる線は連力線といいます)

④連力線と分力の作用線の交点S,Tに直線をひきます。

⑤ ④でひいた連力線を極点を通るように平行移動します。

⑥ ⑤でひいた線とPとの交点をcとします。
ac,cbが分力の大きさです。

⑦連力線①を引いた方に示力図①から出ているacをひきます。

⑧逆の方にcbをひきます。

…これで終了です。
(もう少し詳しくは下のリンクからご覧ください)
「力を平行に分解…えっ意外と面倒くさい?図式解法 算式解法まとめて徹底解説!」
「あぁ~こんなだったわ。」
っていう感じでしょうか?
一つずつ簡単な分野から理解していくことで、これから難しい問題にぶつかったときも解いていくことができます。
しっかりと理解しておきましょう!
次回は算式解法で釣合う力を求めていこうと思います。
ぜひそちらもご覧ください!

