さて今回は片持梁系ラーメンの反力を求めていきたいと思います。
それにあたって片持梁系ラーメンを理解していないといけません。
片持梁系ラーメンについてよくわからない方は以前の記事をご覧ください。
では早速例題を使って考えていきたいと思います。
例題
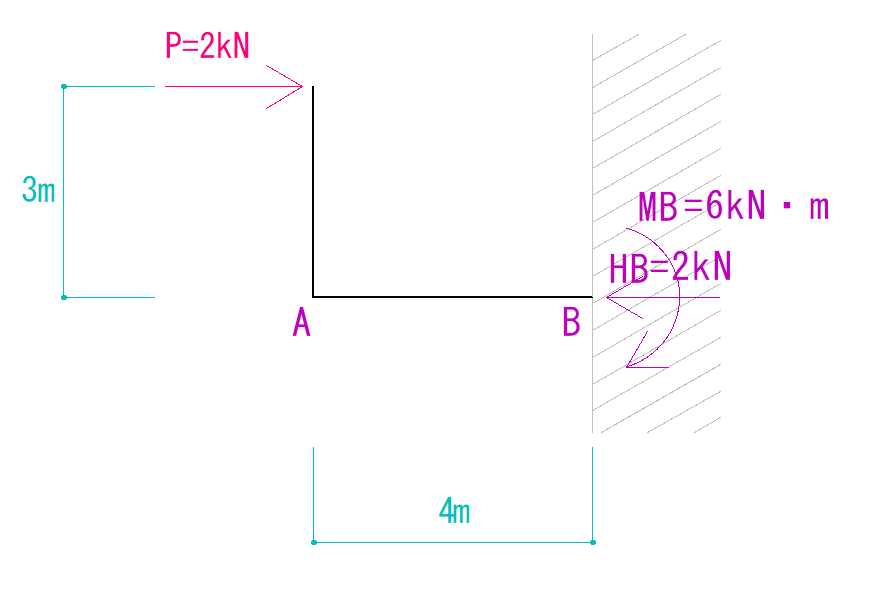
下の図を見て反力をそれぞれ求めなさい。
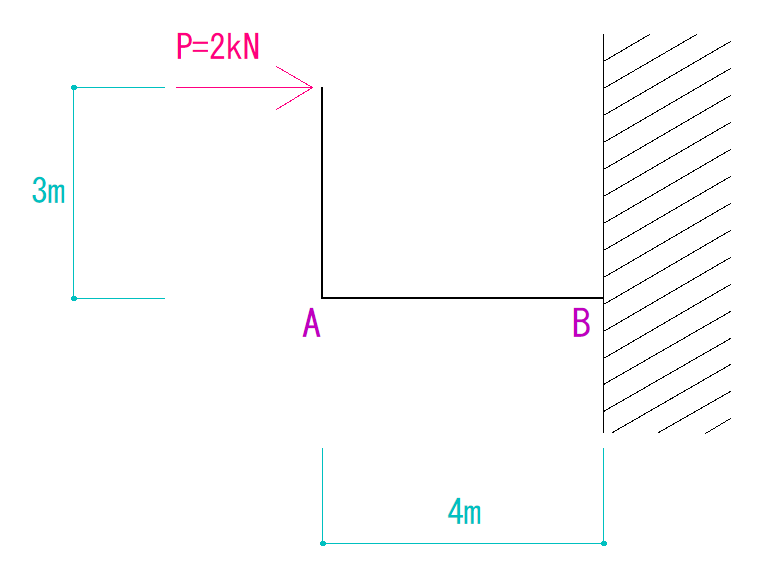
解説
反力の仮定
片持梁系ラーメンの場合、支点は片方の固定端となります。
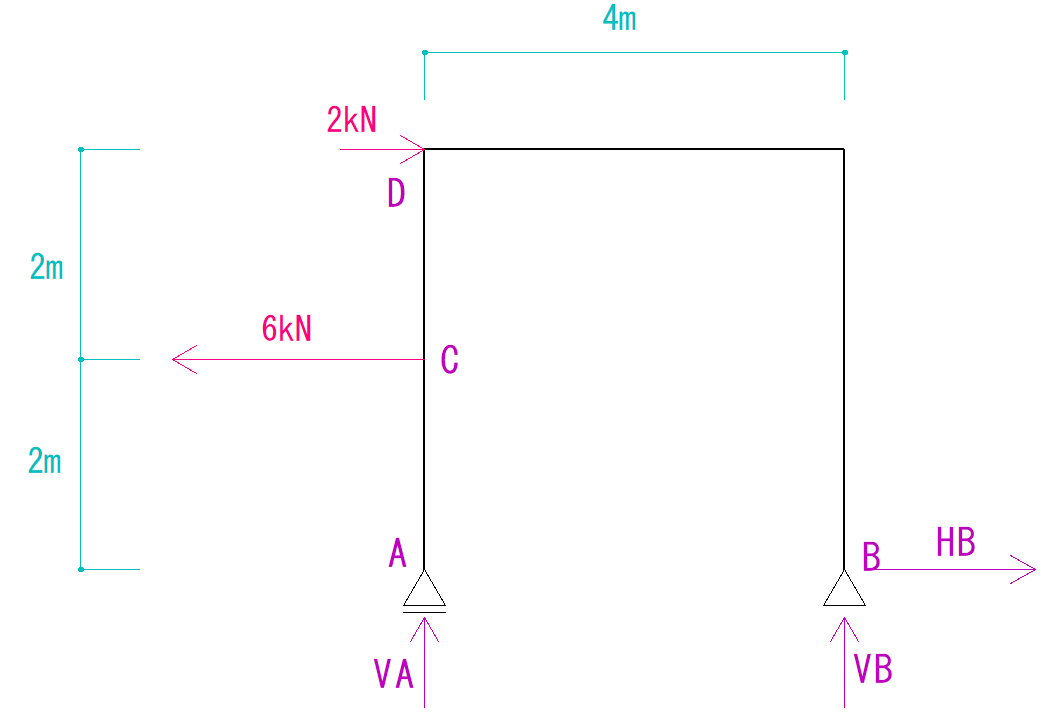
ということは、反力は下の図のように仮定することができます。
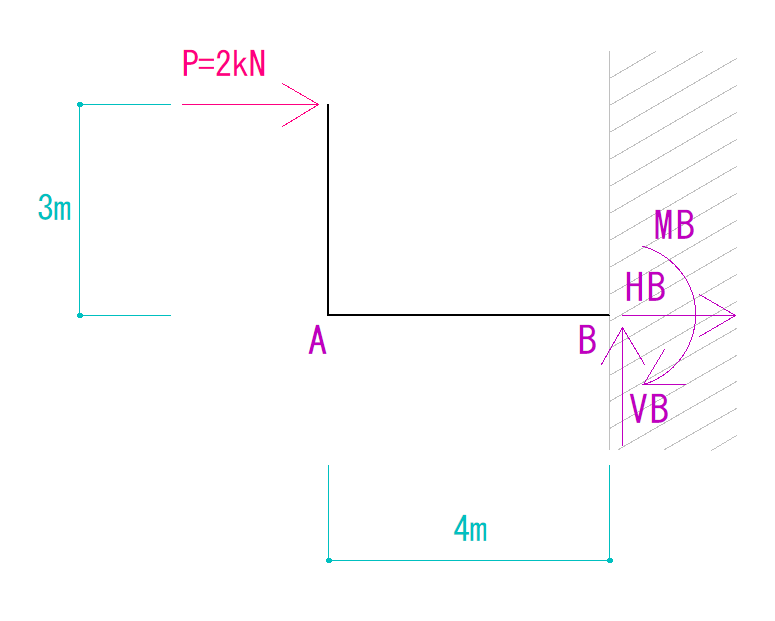
反力について詳しくは下のリンクの記事をご覧ください。
力の釣合いから求める
後はそれぞれの力の釣合い条件を考えます。
一つずつ考えていきましょう。
ΣX=0
まず、X方向にかかっている力だけを見てみましょう。
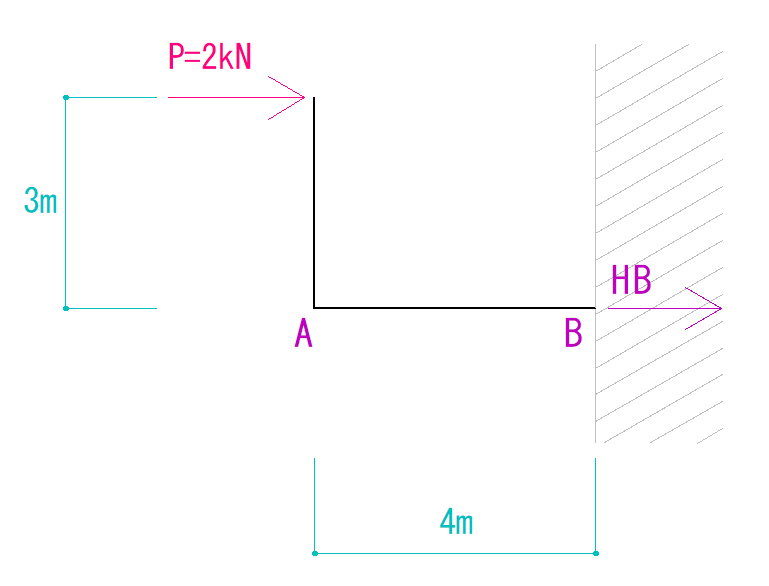
これまで扱ってきた問題では、あまり水平力が出てきませんでしたが、この問題は生じます。
見ただけで直感的にわかるかもしれませんが式に表してみたいと思います。
ΣX=0より、
2kN(P) + HB = 0
HB = -2kN
答えにマイナスが付いたということは仮定とは逆向きとなります。
よって答えは
HB = 2kN(左向き)
となります。
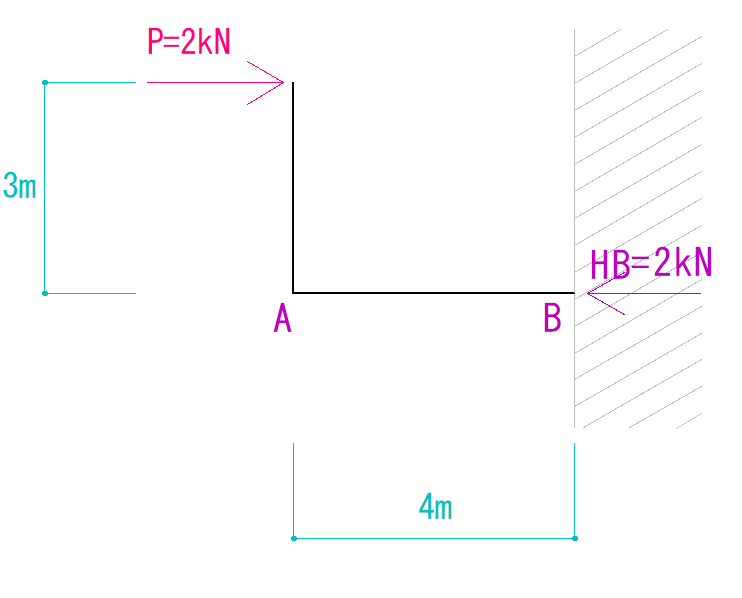
ΣY=0
次にY方向にかかっている力を見てみましょう。
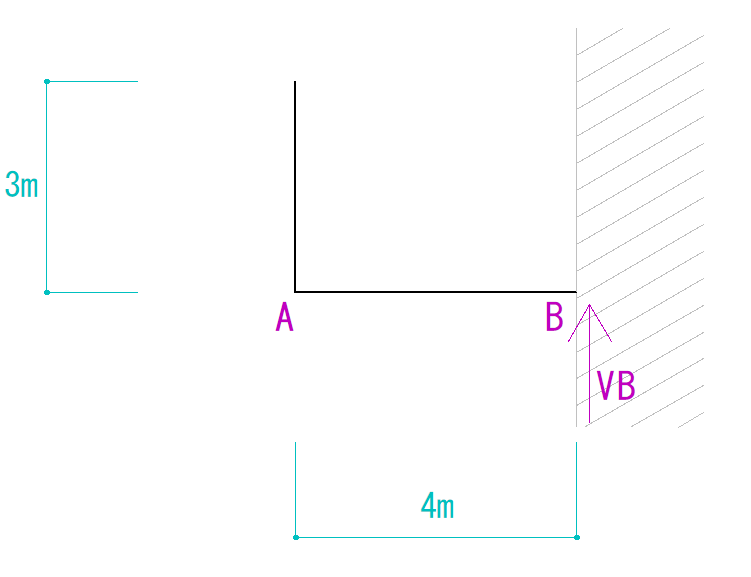
今回はVBのみとなっています。
よって
VB = 0
となります。
ΣM=0
モーメント力の総和も0になります。
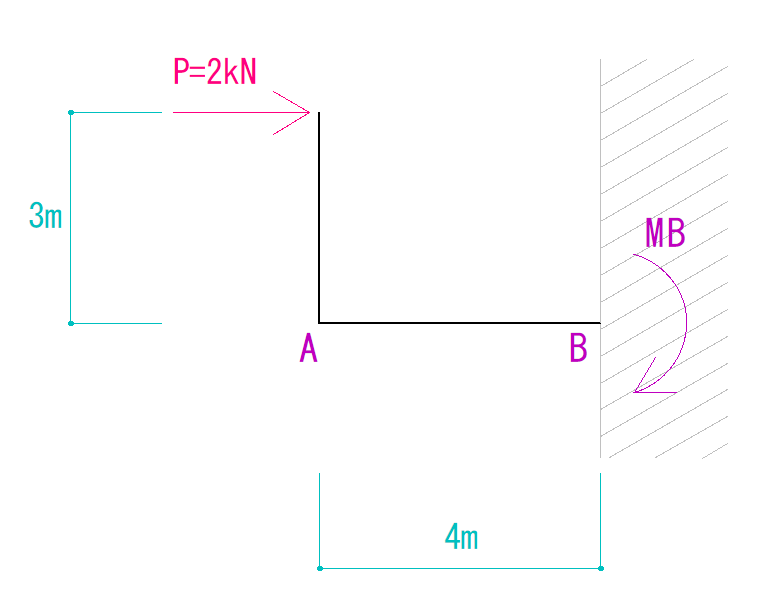
今回はB点を基準に見てみましょう。
まず、B点を回す力を見つけます。
この場合、B点を回す力はMBとPのみです。
(HBはB点との距離0なのでモーメント力を発生させません。)
P点はB点をどれぐらいの力で回すでしょうか?
力×距離だから2kN × 4m … としてはいけません!
モーメント力の公式をもう一度確認しましょう。
力のモーメントの公式
M=Pl[N・㎜,N・m,kN・m など]
P…力の大きさ
l…力Pの作用線までの垂直距離
となっています。
「l」は何を表しているでしょうか?
ただの距離ではありません。
垂直距離です。
つまり、力の作用線を伸ばしたときに、作用点と最短距離になるときの距離を入れなければなりません。
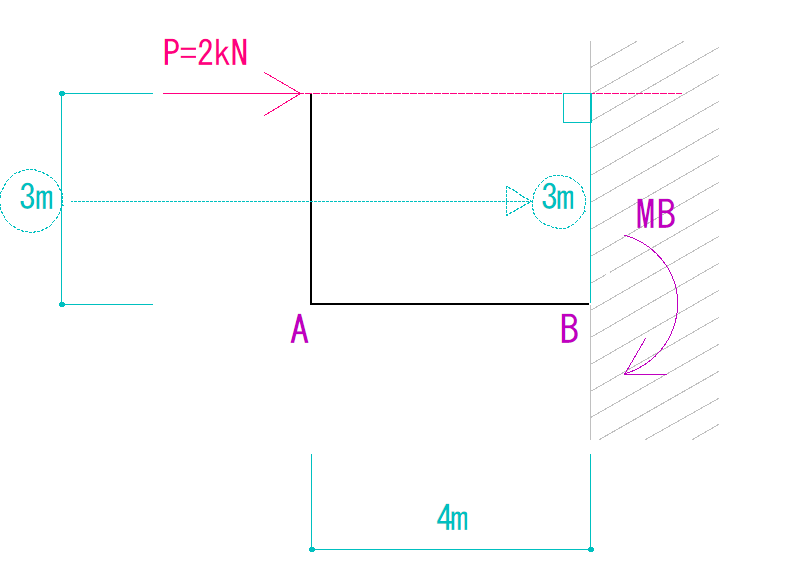
今回の問題の場合は3mということになります。
よって、PがB点を回す力は
2kN × 3m = 6kN・m
反時計回りのためマイナスをつけて、
-6kN・m
となります。
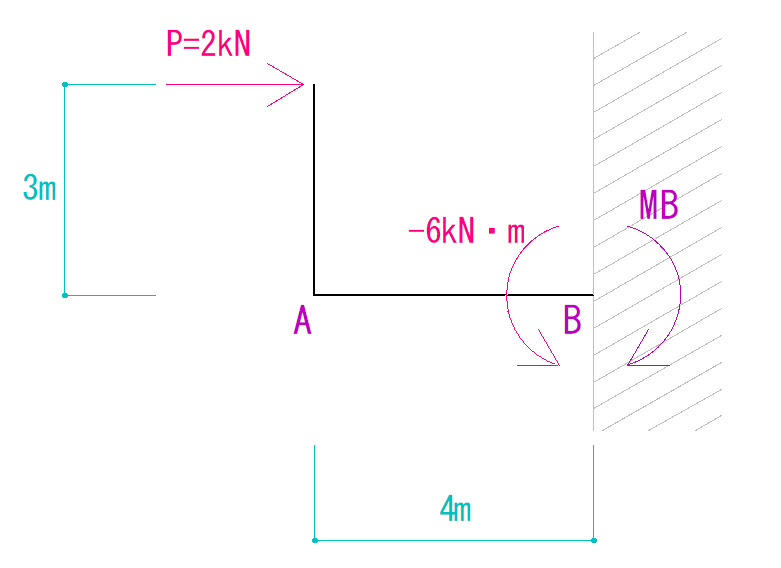
ΣMB=0より、
-6kN・m + MB = 0
MB = 6kN・m(時計回り)
となります。
答え
HB = 2kN(左向き)
VB = 0
MB =6kN・m(時計回り)
となります。