さて、力の合成のやり方について今回は説明していきたいと思います。
力の合成ってなに?と思った方は前の記事をご覧ください。
「力の合成とは」
力の合力を出す方法は大きく分けて二つあります。
作図方法(図式解法)と計算方法(算式解法)です。
【力の合成】作図方法(図式解法)
まずは図式解法についてです。
教科書などには図式解法として二つのやり方が載っている場合があります。
「力の平行四辺形」を利用する場合と「力の三角形」を利用する場合です。
正直二つに分ける必要あるのか分からないぐらいやり方は類似しています。
結局答えが出ればいいので覚えやすい方を覚えてください。
ただ、後々のことを考えると力の三角形を利用する方で慣れておくことをお勧めします。(個人的な意見ですので先生方のやり方に沿って覚えてください)
一応やり方を教科書で分けられている以上ここでも両方解説します。
下の図の問題でそれぞれ考えていきましょう。
例題
P1,P2の合力Rを求めよ。

【力の合成】力の平行四辺形を利用する場合
①B点からP1に平行な直線を引きます。

②A点からP2に平行な直線を引きます。

③できた平行四辺形の対角線をひきます。

その対角線が二つの力の合力です。
【力の合成】力の三角形を利用する場合
①B点からP1に平行で同じ大きさと向きが等しいP1´(BC)をひきます。

②OCをひきます

これが二つの力の合力です。
さて、なんでこれが二つの合力といえるのか。
それは細かくなってきますので後々解説したいと思います。
いまはこういうものだ、という程度にしておいてください。
【力の合成】計算方法(算式解法)
さて次は算式解法について解説していきたいと思います。
算式解法ですが、ここでは力の作用線が直角の場合についてです。
直角以外のパターンもありますがここでは解説しません。
(直角以外の場合かなり難易度が上がります。学校によっては算式解法自体、授業で触れるだけでテストには出ないというところもあるかもしれません。)
まず、公式がありますのでそれを覚えましょう。
【力の合成】公式

Px…X方向に作用する力の大きさ[N,kN]
Py…Y方向に作用する力の大きさ[N,kN]
ルートが出てきて見るからにややこしい感じがしますね。
確かにこれをこのまま覚えようとするとよくわからなくなるかもしれません。
でも実はこれって、ある公式と同じなのですが気が付きましたか?
それは三平方の定理です!
関連記事はこちらをチェック↓↓↓
あ~言われてみれば…という感じでしょうか?
三平方の定理は直角三角形の斜辺の長さを出すときに使う公式ですよね。

なぜ三平方の定理と合力を求める式が同じになるのか。
言葉で書いてもなかなか伝わらないと思うので図で確認してみましょう。

図を見ると三角形の斜辺の大きさと合力の大きさが同じだということがわかるでしょうか。
そのため公式は三平方の定理と同じ式になっているのです。
また算式解法では合力とX軸のなす角度を求めます。
公式を確認しましょう。

Px…X方向に作用する力の大きさ[N,kN]
Py…Y方向に作用する力の大きさ[N,kN]
これも三角形の角度を求める公式と同じです。
では例題から考えてみましょう。
例題
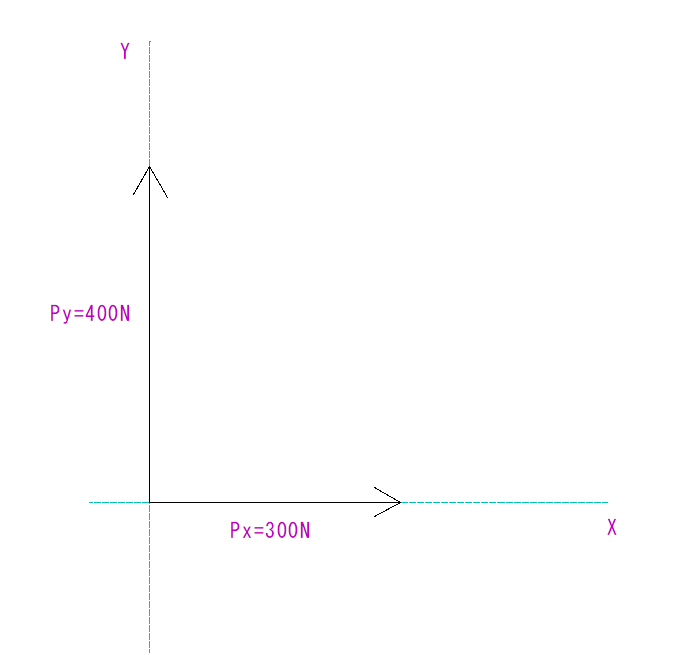
下の図を見て合力Rの大きさとX軸とのなす角度θの値を求めなさい。

解説
まず合力を求めます。
公式より

=13kN
次になす角度を求めます。

=2.4
関数電卓を使い、角度を出します。

したがってθ=67.4°となります。
少し難しくなってきましたが、合力というよりも三角形の斜辺をだすというイメージでやるといいかもしれません。
宿題
下の図より算式解法にて合力の大きさとX軸とのなす角度を求めなさい。
答えは次の記事「力の分解 図式解法 算式解法」に書いてあります。