今回は単純梁に等分布荷重がかかった場合のQ(せん断力)図M(曲げモーメント)図の描き方を解説していきたいと思います。
この解説をするにあたって、等分布荷重というのが何かわからないと先に進めません。
復習しておきたい方は下のリンクから見ることができます。
例題
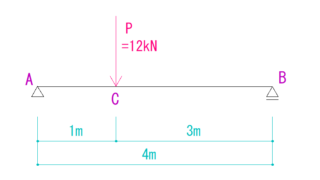
下の図を見てQ図M図を求めなさい。

解説
反力の仮定
まずは反力を仮定し、求めていきます。
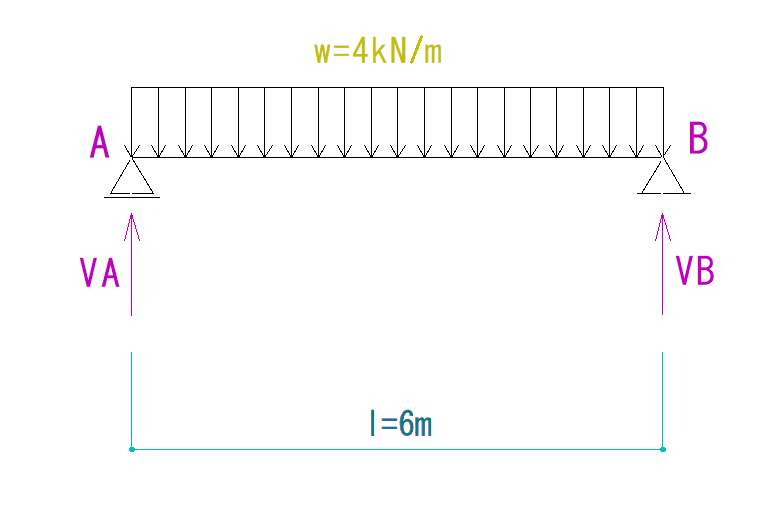
この問題では水平力が働いていないため、水平反力及びN図は省略します。
それでは反力を求めていきます。
まず、このままだと計算がしづらいので等分布荷重の合力を求めます。
等分布荷重の合力の大きさは、
等分布荷重がかかっているところの距離[l]×等分布荷重の厚さ[w]
でした。
なので今回の合力は、
6×4=24kN
となります。
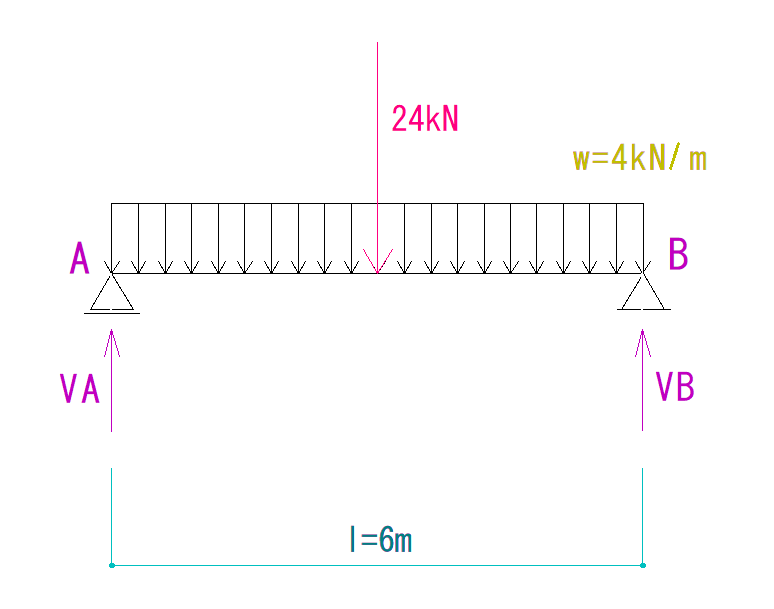
合力のかかる位置は分布荷重の重心です。
重心…と聞くと難しいですが、等分布荷重の場合真ん中になります。
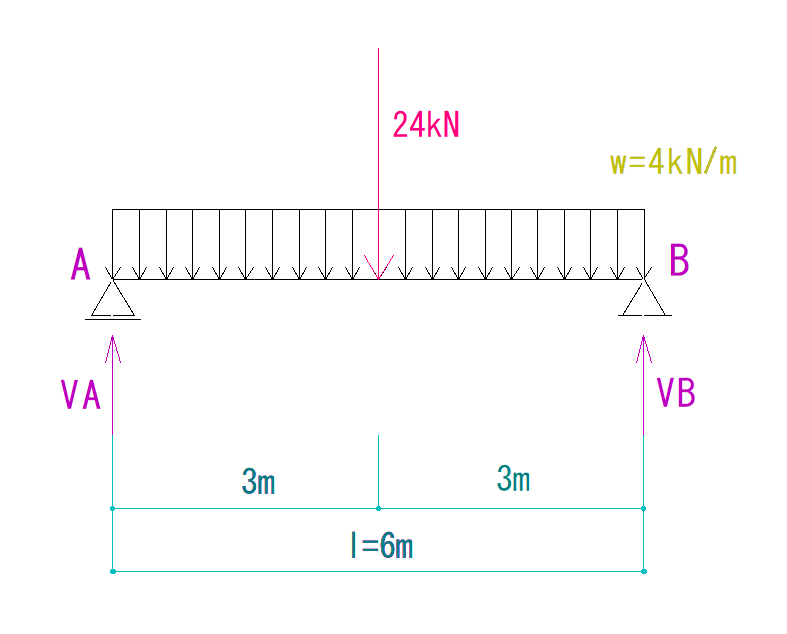
ここまでくると見慣れた形になりました。
あとは力の釣合い条件を使って反力を求めていきます。
単純梁に集中荷重がかかった場合の反力の求め方は下の記事を参照
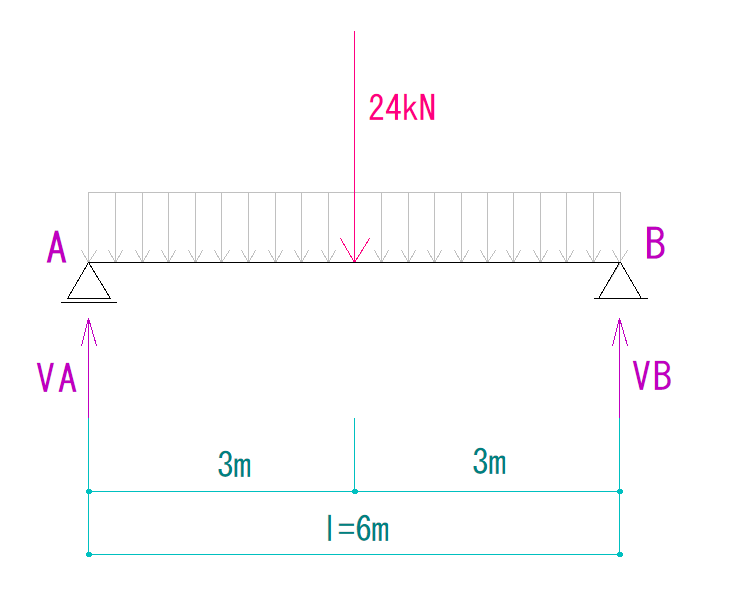
A点をO点としてΣMAを考えると、
(-VB×6)+(24×3)=0 …※
-6VB=-72
VB=12(仮定通り上向き)
となります。
※(なぜVBにマイナスが付いているかというと、仮定の向きではA点を反時計回りに回すためです。)
ΣY=0より
VA+(-24)+12=0
VA=12(仮定通り上向き)
となります。
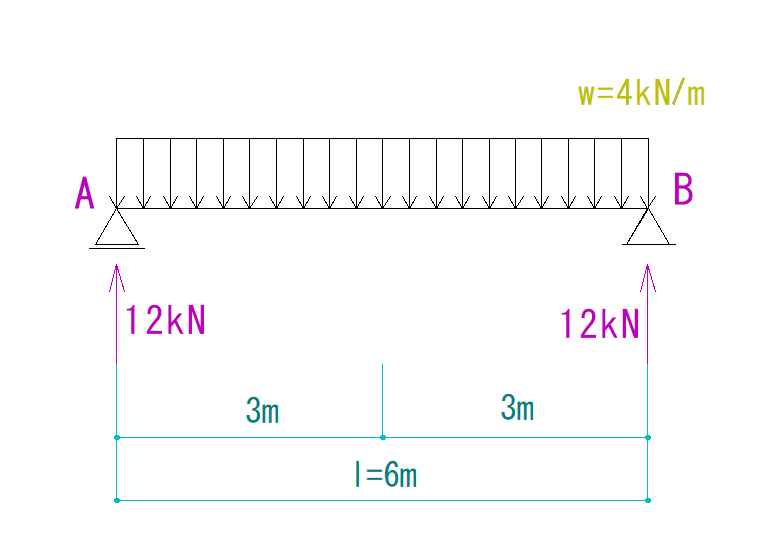
Q図の描き方
それではQ図から書いていきましょう。
やり方は覚えているでしょうか?
問題を右(もしくは左)から順番に見ていきます。
詳しいやり方は下の記事を参照
「建築構造設計の基礎であり難関 N図,Q図,M図の書き方を徹底解説!」
さて、A点を注目してみましょう。

部材の左側が上向きの力でせん断されています。
この場合符号は+と-どちらでしょうか?
下の表で確認しましょう。
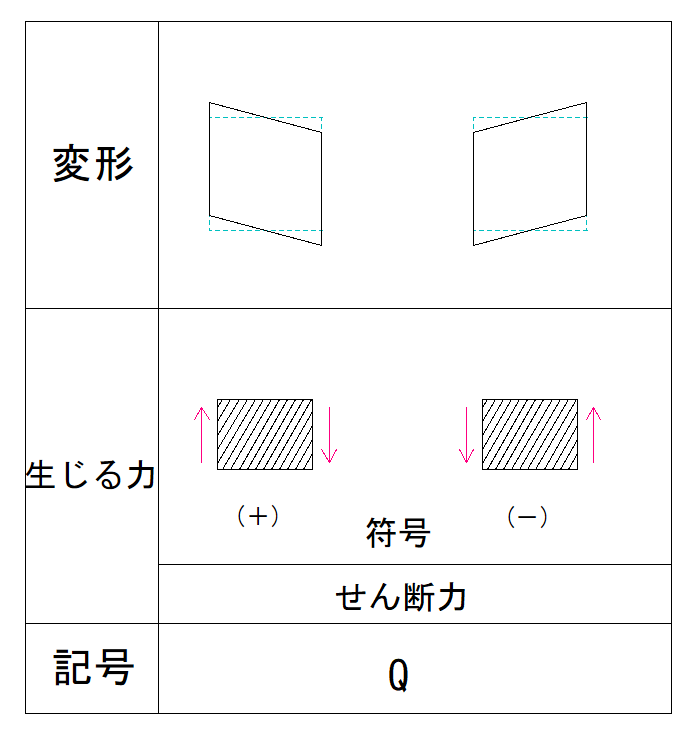
部材の左側が上向きの場合、符号は+となります。
大きさはVAのまま12kNとなります。

実はここからが問題です。
集中荷重の場合は視点をずらしていって、次に荷重がかかるところまでいきました。
しかし、今回はずーっと荷重がかかっています。
その場合、等分布荷重の終了地点に目を移します。
今回はB点です。
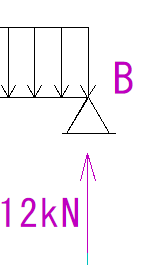
部材の右側が上向きの力でせん断されています。
この場合符号は+と-どちらでしょうか?
下の表で確認しましょう。

部材の右側が上向きの場合、符号は-となります。
大きさはVBのまま12kNとなります。

ここで一つ覚えておいてください。
等分布荷重のQ図は直線になります
つまり、等分布荷重の端と端の大きさが分かれば、あとはそれを繋ぐように線を引くだけでいいということです。
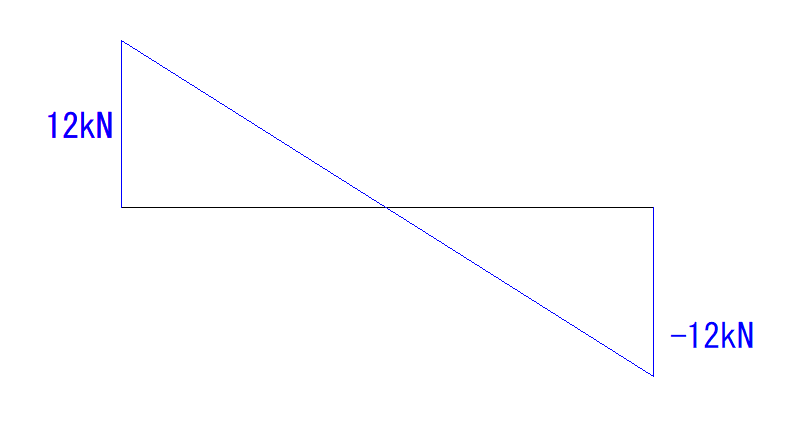
これで完成です。
大きさと単位を入れましょう。
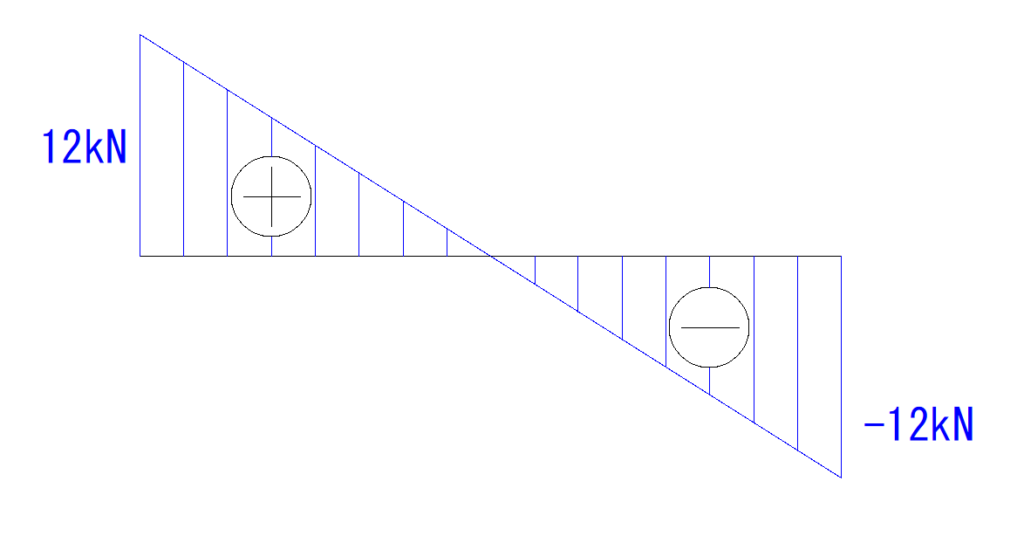
補足:なんでQ図は直線になるの?
なぜ等分布荷重の端と端の大きさが分かれば、あとはそれを繋ぐように線を引くだけでいいのでしょうか。
一つずつ考えていきましょう。
まず問題を4分の1に分けてみます。
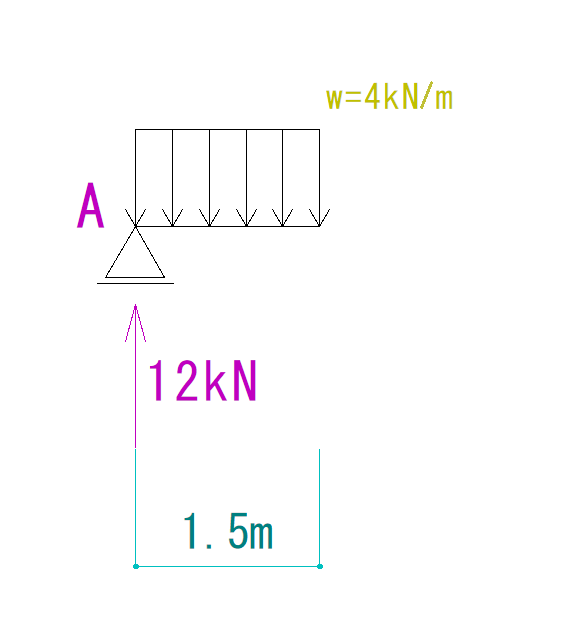
この時の等分布荷重の大きさと合力のかかる位置は下の図で確認ください。
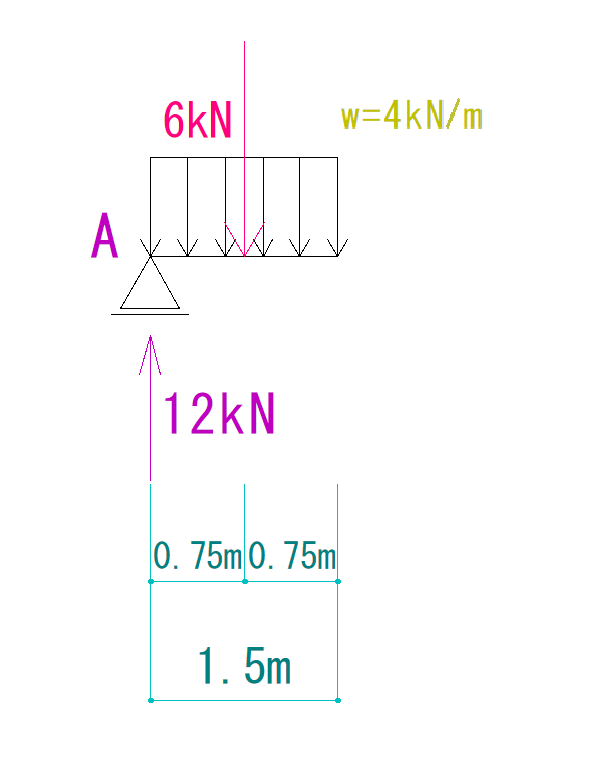
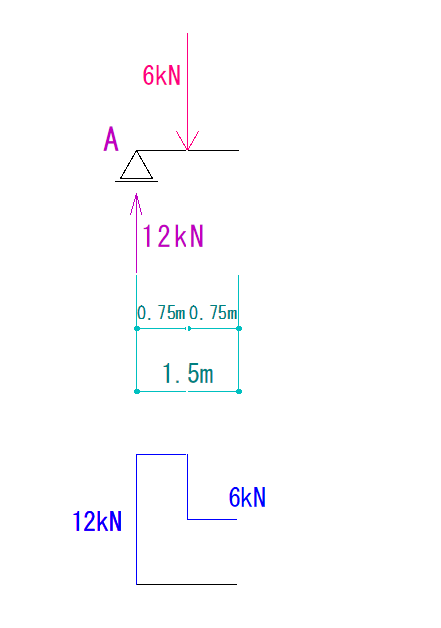
もし、この合力とVAでQ図を書く場合Q図は下のようになります。
そしてこのように例題の等分布荷重を4分の1ずつに分けた全体のQ図が下の図です。
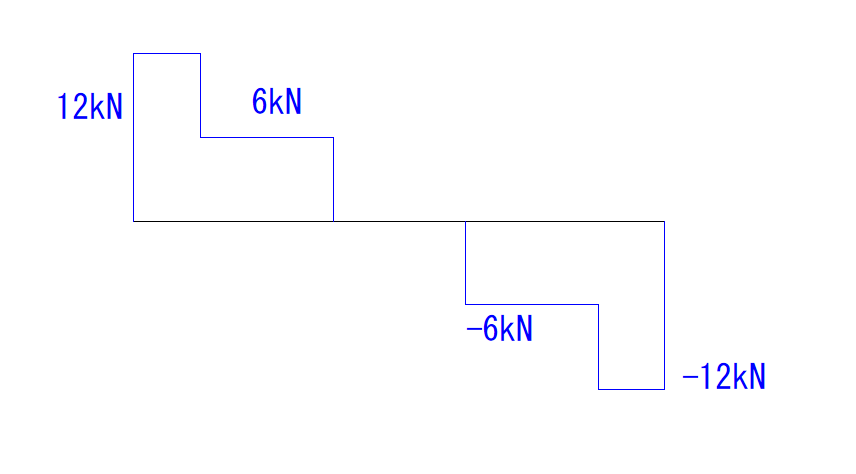
では16分の1にするとどうなるでしょうか。
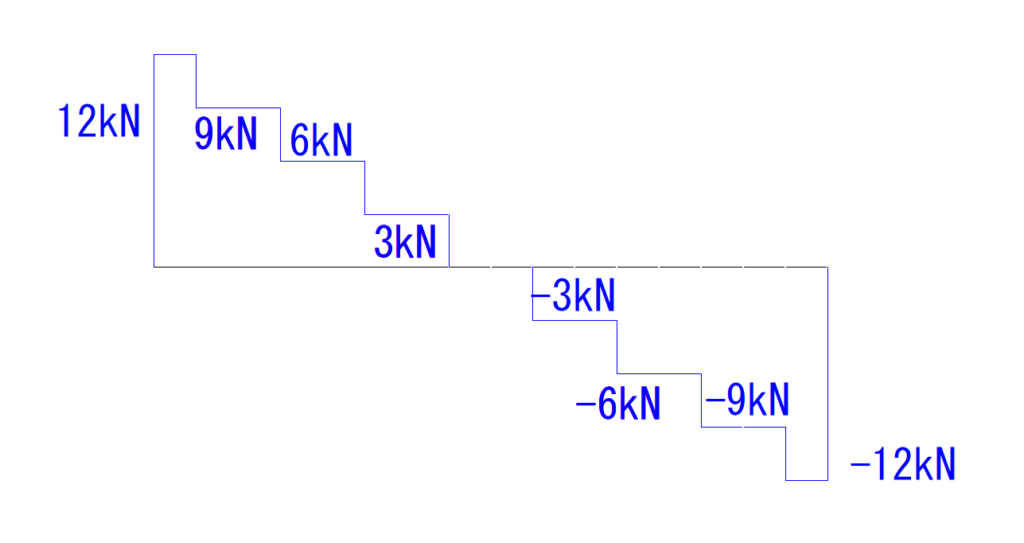
先程より細かくなります。
では32分の1は…

と、ここまでくるとわかるでしょうか。
等分布荷重を細かく分けていくとどんどん直線系になります。
そのためQ図は端と端を繋ぐ直線の形になるのです。
M図の描き方
次にM図を書いていきましょう。
先に言っておきますが、M図の形は2次曲線の形になります。
…急に数学!と思うかもしれませんが、仕方ありません。
理由はQ図がなぜ直線になるのか、のところで解説したのと同じなのですが、細かくしていくと2次曲線の形になるからです。
(式を組み立てていくとわかるのですが、任意距離xの値を2乗しています。そのため2次関数の形になります。数学が得意で時間がある方は自分で確認してみてください。)
ただ、フリーハンドで正確な2次曲線は書けません。
なので、大体2次曲線の形になっていれば正解になります。
ただ、符号と最大値は求める必要があります。
符号の求め方
これは計算とかしなくても、なんとなくわかるかと思います。
下の表で確認してみましょう。
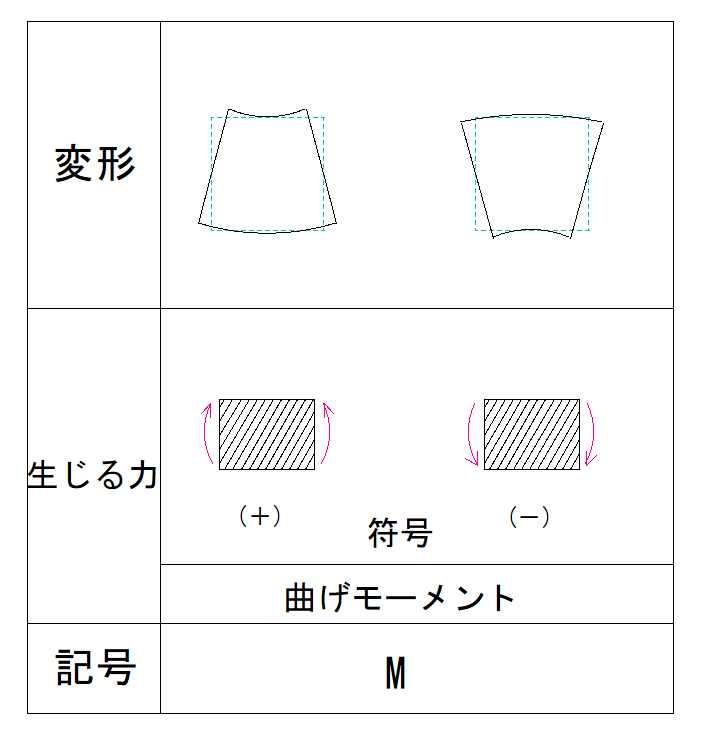
今回は符号+になります。
maxMの求め方
どこの地点でM値が最大になるでしょうか?
これも計算しなくても、なんとなく真ん中かなぁ…と分かると思います。
しかしこれから複雑になるときに覚えておくときに便利な法則があります。
それは、
Q値が0の時がM値最大
ということです。
Q図でプラスからマイナスに変わるところがMの値が最大になります。
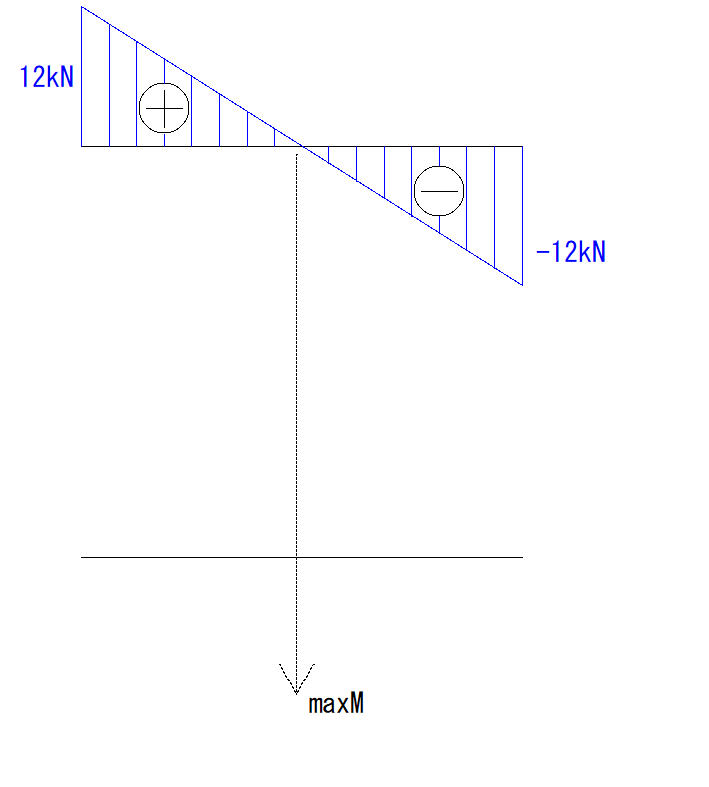
では最大M値を求めていきましょう。
まず、Mが最大地点のところより左側(右側でも可)だけを見ます。
そこに見えている力の合力が、Mの最大地点をどれぐらいの大きさで回すのかを計算します。
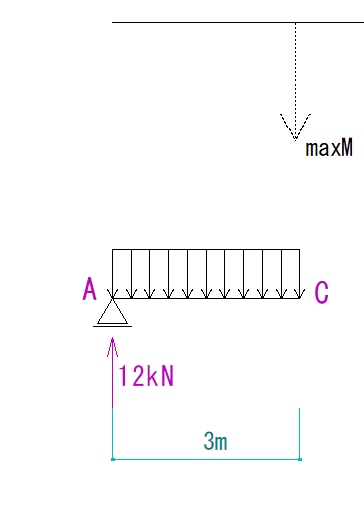
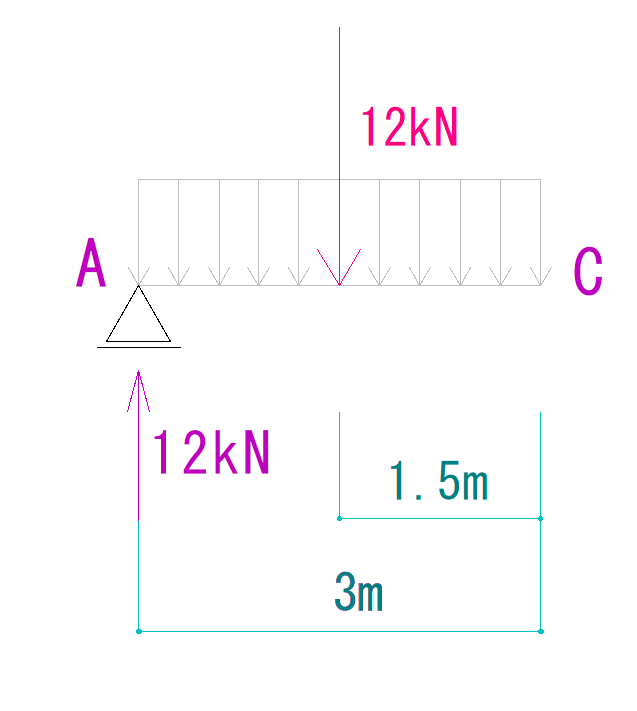
今回はVAと等分布荷重の半分のΣMCを求めます。
式で表すと…
12kN×3m+(-12kN×1.5m)
=36-18
=18kN・m
となります。
そうしたらC点に+18kN・mのところに点を打ちます。(任意地点)
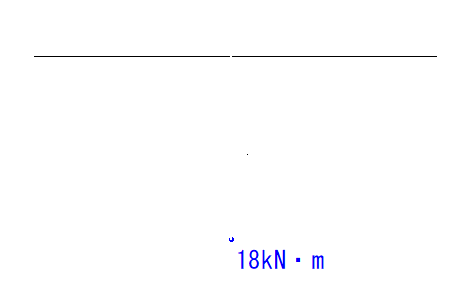
A点B点はM=0なので、この3点を通る2次曲線を描きます。
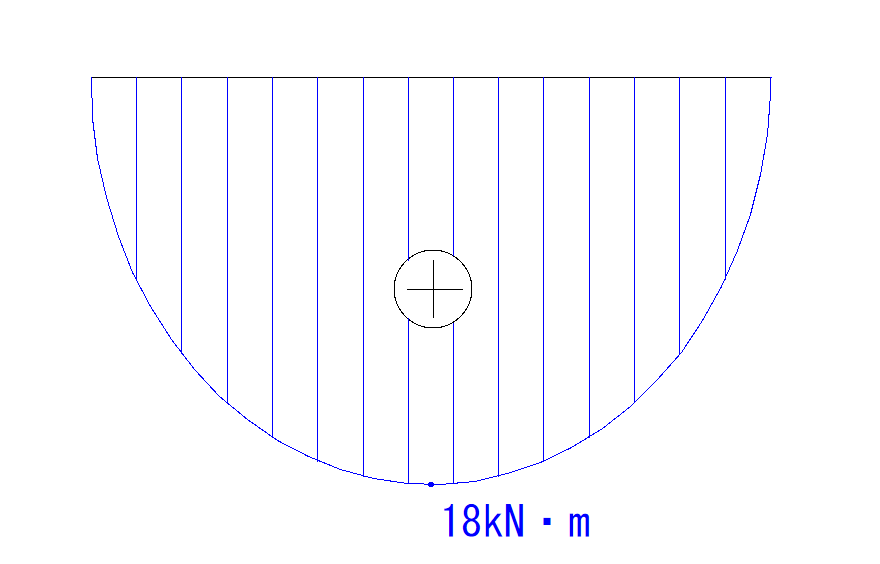
最後に最大値と符号を書き込んで完成です。