今回は構造設計の中でもこれからの肝となるN図,Q図,M図(軸方向力図,せん断力図,曲げモーメント図)の書き方について解説していきたいと思います。
そもそもN図Q図M図ってなんなのか謎ですよね。
N,Q,Mとはそれぞれ何を表しているのかというのは前回の記事で見ることができます。
では、早速書き方を解説していきたいと思います。
例題
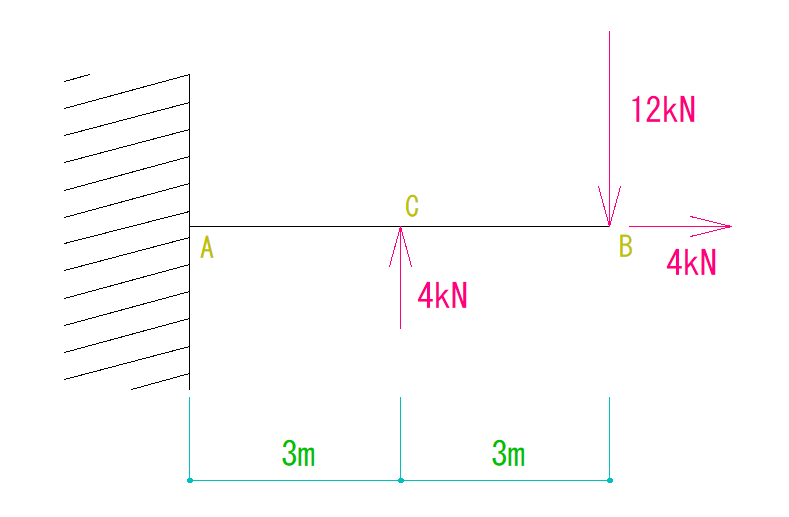
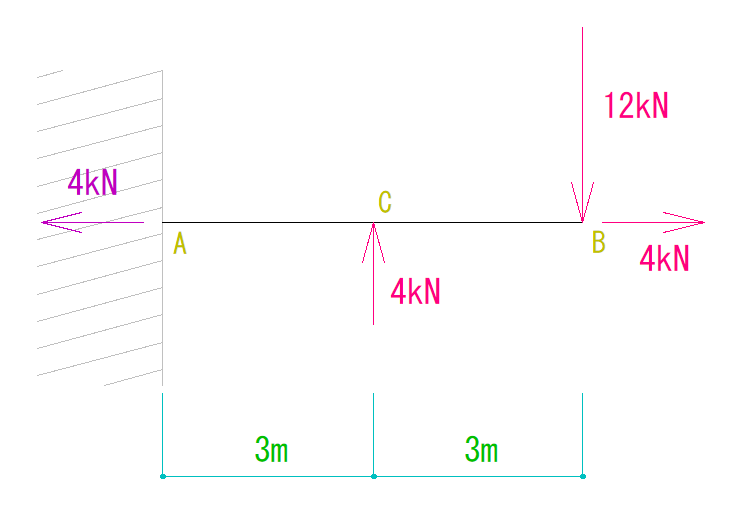
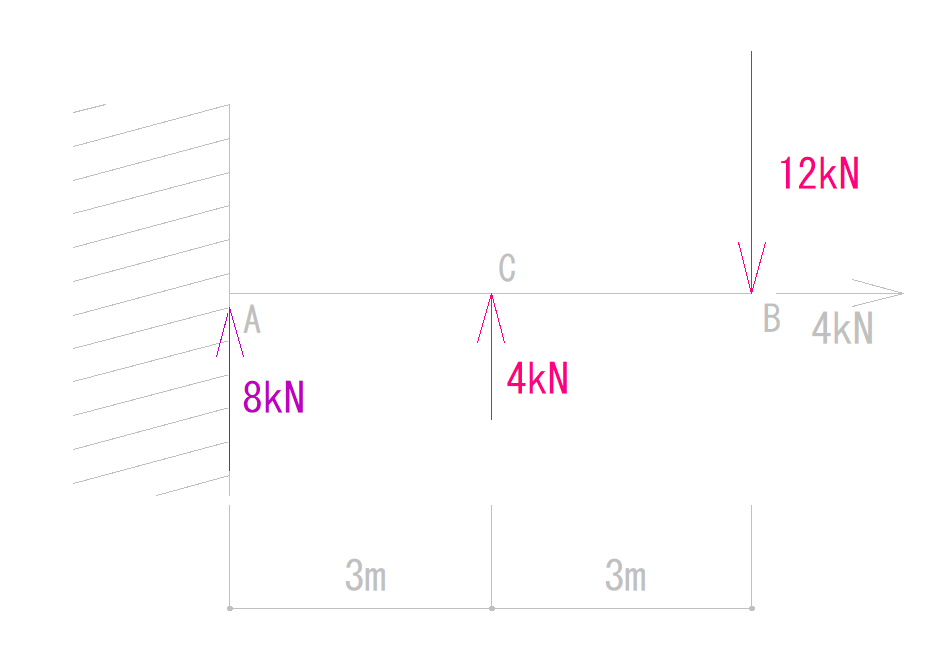
下の図をみてN図Q図M図を書きない。
N図(軸方向力図)の書き方
まずは水平方向の反力を求めます。
ここでの水平反力は簡単ですね。
式は省略します。
4kN(左向き)となります。
では、水平にかかっている力に注目してみましょう。

構造物を互いに引っ張り合っています。
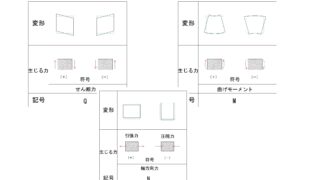
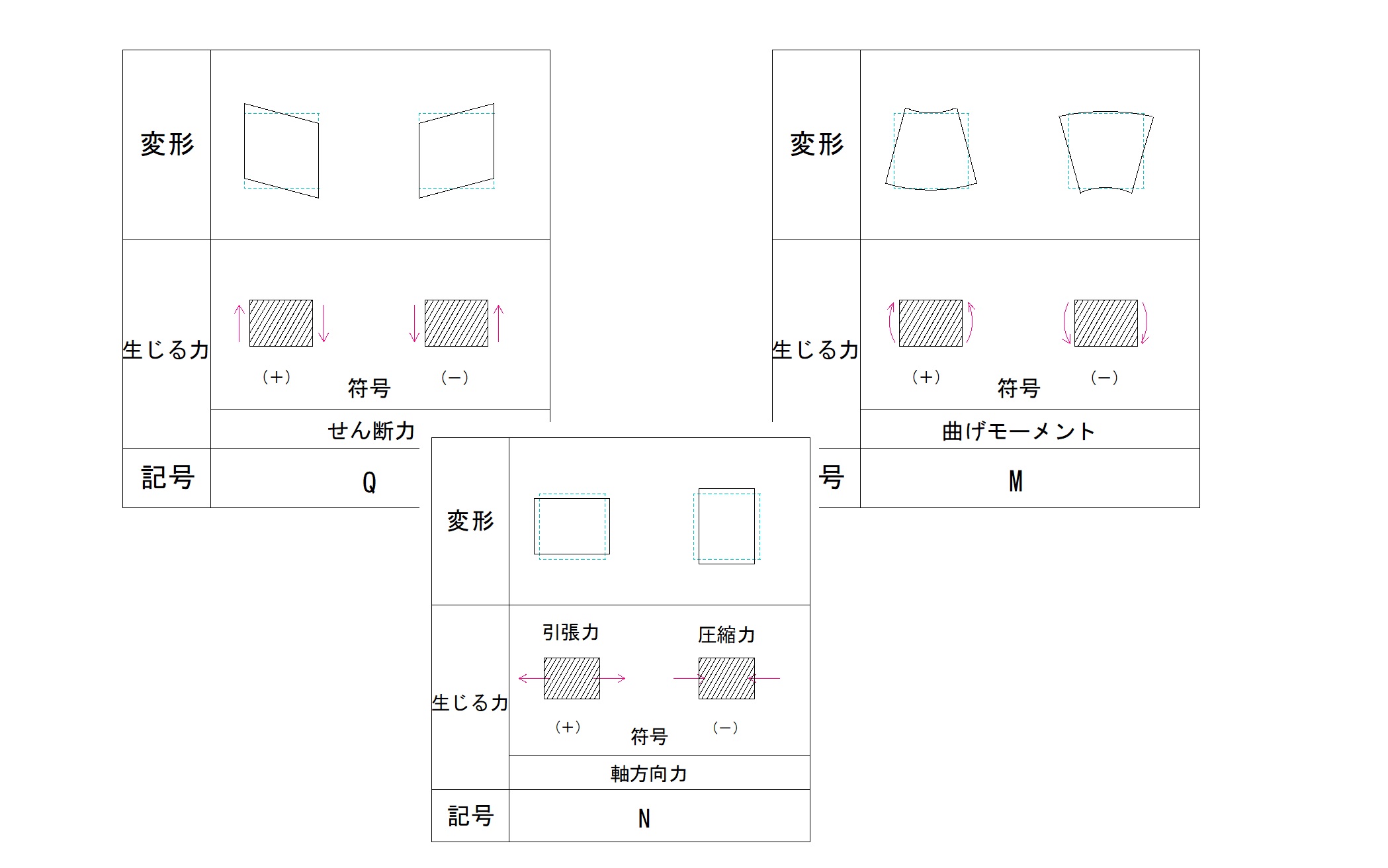
この時、符号は+と-どちらになるでしょうか?
下の表を見て確認しましょう。
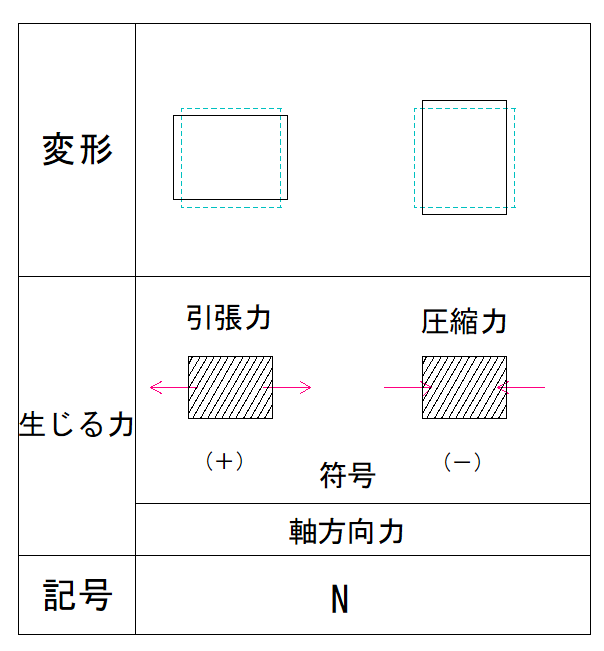
この場合符号は+になります。
さて、材料はそろいました。
N図を書いていきましょう。
N図書き方手順
スタートは下の図のようになっています。
基本ですが、この線の上側が+,下側が-になっています。
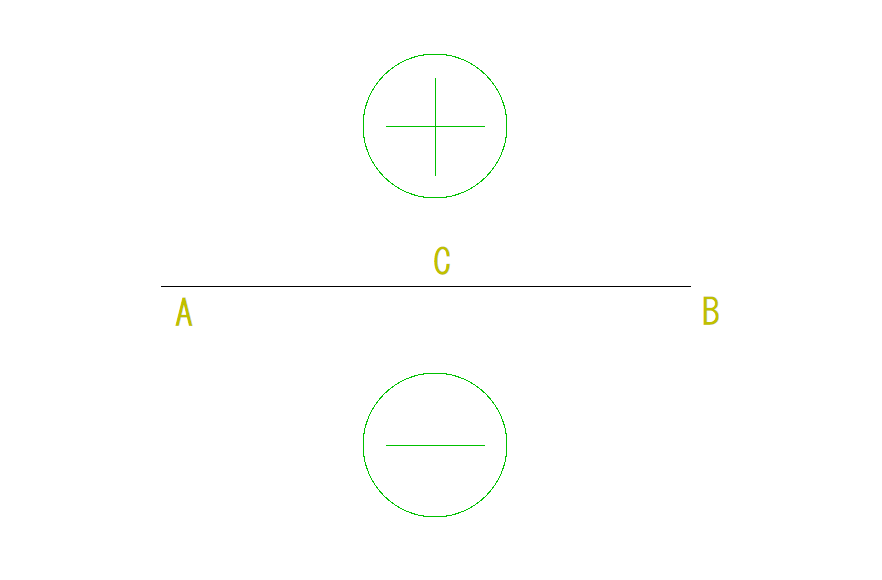
今回の場合は符号が+なので上側に出ることになります。
どれぐらい出っ張るのか、これは自分の匙加減です。

この問題では、構造物の端と端を引っ張り合っているので、構造物にはどの地点でも等しい力の引っ張り力が働いています。
それを図に表すとこのようになります。

部材のどの点を取っても引っ張り力は変わらない、ということですね。
最後に大きさと符号を書き入れれば完成です。

N図の場合、途中で力が変わることはあまりないので、基本的に真四角の図になることが多いです。
Q図(せん断力図)の書き方
まずは鉛直方向の反力を求めましょう。
これも簡単なので式は省略します。
VAは8kN(上向き)となります。
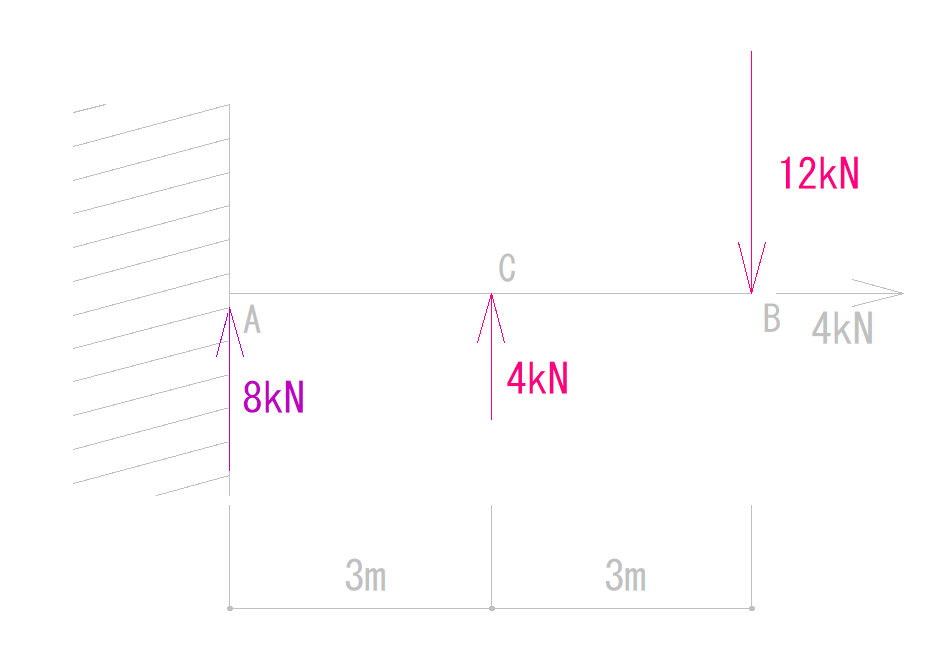
Q図を書く時のポイントは、左から(右からでも可)順にみていくことです。
細かく説明しましょう。
Q図書き方手順
A点より右側を手で隠してみてください。

A点には上向きの力がかかっています。
部材の左側に上向きの力があるせん断力の符号は+と-どっちでしょうか?
下の表で確認してみましょう。
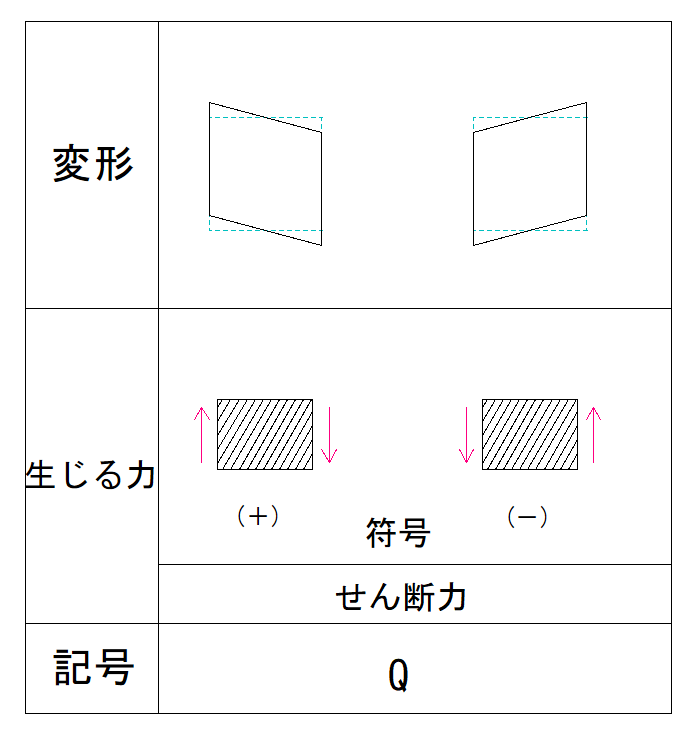
部材の左側が上向きなのは+ですね。
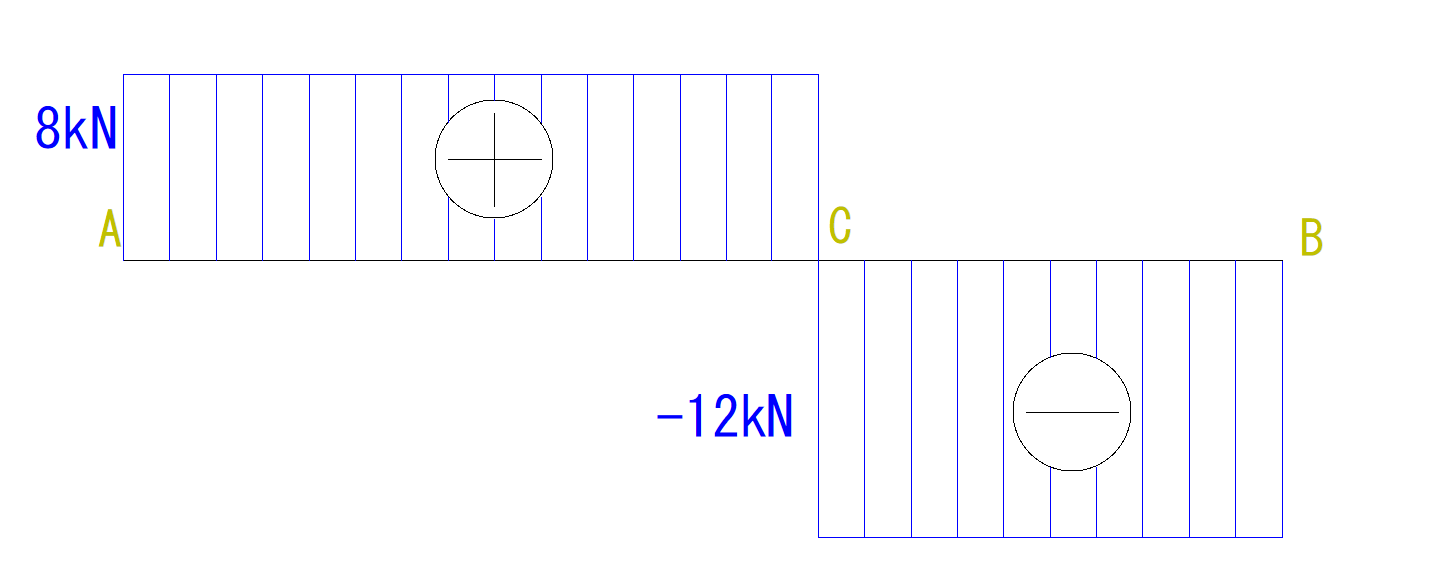
なので、図のA点のところをプラス方向に8kN突き出します。
大きさは任意です。

そこから徐々に隠している手を右にずらしていくと、C点が見えます。

そうしたらA点とC点のせん断力を合計します。
今回はどちらも+なので、足して12kNとなります。
図はどのように書けばよいでしょうか?
今は8kNですが、C点でさらに+方向に4kN突き出ます。

大きさは、定規ではからなくてもよいですが、大体8kNの半分ぐらい出るのをイメージしましょう。
また徐々に手を右に動かしていくと最後のB点まで行きました。
ここまで来たら、図も最後に0の基準の線まで落として終わりです。

最後に、それぞれの出っ張りに大きさを書き入れ、図に符号を書き入れましょう。

Q図のコツは左(もしくは右)から順にみていくことです。
慣れてきたら手で隠さなくても、イメージでできると思います。
また、Q図はせん断力の力が加わるところでしか、図は変化しません。
集中荷重の場合、図は四角を組み合わせたような形になります。
M図(曲げモーメント図)の書き方
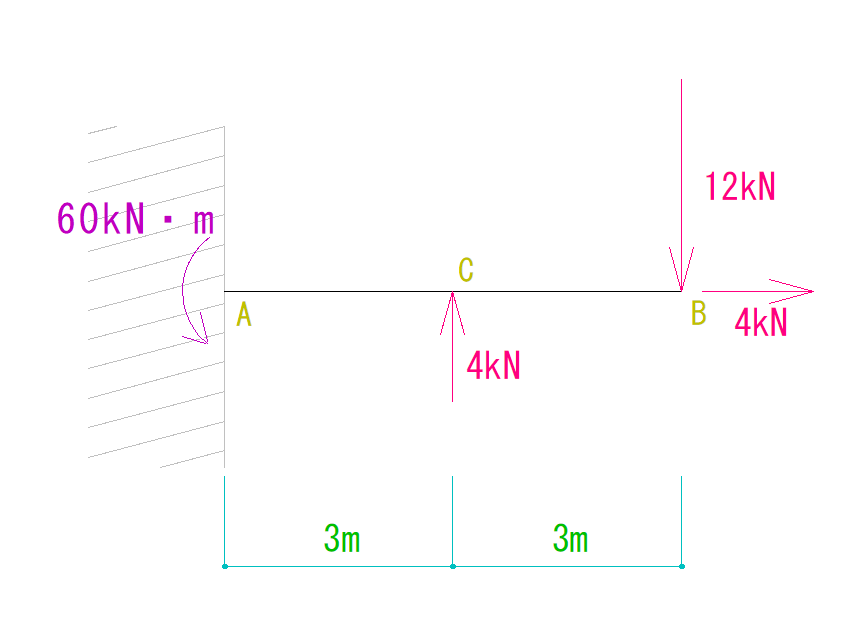
まずはモーメントの反力を求めましょう。
これも簡単なので式は省略します。
RMAは60kN・m(反時計回り)となります。
ここで一つ注意点です!
M図は+と-が反対になります!
線より下が+で上が-ということです。

しっかりと確認しましょう。
M図書き方手順
M図では、モーメント反力がない方から順にみていくのがセオリーです。
今回の問題では、B点にモーメント力がないので、右から見ていきます。

最初ですが、B点にはモーメント力がない、つまりスタートは0です。
(それぞれの力はB点を押したり引いたりしていますが、回してはいません)
ここで徐々に左の方に目を移していきます。
そしてC点のところで一回ストップします。

C点にはどれぐらいのモーメント力が働いているでしょうか?
B点に加わっているP1がモーメント力をかけています。
モーメント力の計算方法は下の記事を参照
式は簡単なので省略します。
計算すると、C点にかかっているモーメント力は36kN・m(時計回り)となります。
ここでまた、符号の問題です。
構造物の右側が反時計回りの場合の符号は+と-どちらでしょうか?
下の表で確認してみましょう。
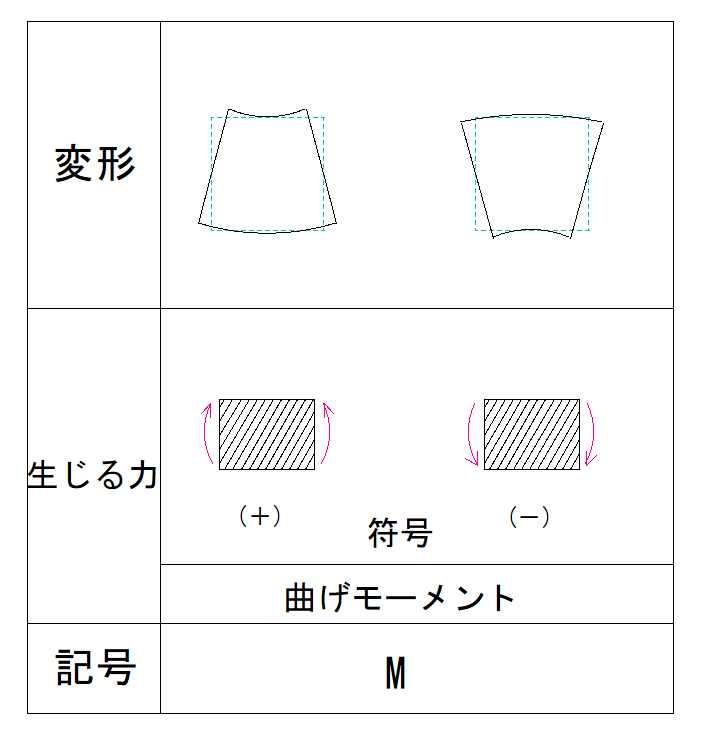
部材の右側が反時計回りのモーメント力の場合、符号は-となります。
そこで、図のC地点の-側の適当な場所に点を打ち、ここが36kN・mということにします。
そしたら、その点とB地点の0を直線で結びましょう。

次に目を左に移していくと、A点があります。

A点にかかるモーメント力はいくつでしょうか?
これは反力を求めるときにすでに計算しましたね。
大きさは60kN・mとなります。
符号は-のままとなります。
図のA地点に点を打って線を繋ぎます。

ここで注意なのは、C点からA点が、B点からC点の角度より緩くなるようにすることです。
最後に符号を書き入れて、それぞれの地点に大きさを書き入れて完成です。

集中荷重のM図では、力が加わったときだけ角度が変わります。
そのため、形は三角形っぽくなります。
まとめ
どうだったでしょうか?
これからの構造設計はよくN図Q図M図を求められます。
一個前の記事と一緒に、しっかりと理解しておきましょう。