さて、先回は作用点の違う力の釣合い図式解法について考えることができました。
まだ見ておられない方は下のリンクから見ることができます。
「作用点の違う力の釣合いについて解説!釣合うには回ってもいけません!図式解法」
今回は算式解法について考えていきたいと思います。
【作用点の違う力の釣合い】解説
まずは作用点の違う力の釣合い条件について振り返りましょう。
(図式解法の記事で確認したことですが、今一度振り返ってみます)
【作用点の違う力の釣合い】釣合い条件
…と言っても何か大きく変わることはありません。
ΣX=0
ΣY=0
に加えて、一つだけ新しい釣合い条件が出てきます。
復習ですが、釣合いとはそれぞれの力を合わせた時にバランスがとれていることです。
このバランスという中には、横に動かない、縦に動かないだけではなく、回らない、という意味があります。
つまり、加わる釣合い条件は
ΣM=0
です。
(ΣM=0とは物体に働くモーメント力の合計が0になるという意味です。
モーメントについては下の記事で詳しく解説しています。)
言葉で書かれてもよくわからないと思うので、例題を使い確認していきましょう。
【作用点の違う力の釣合い】 例題
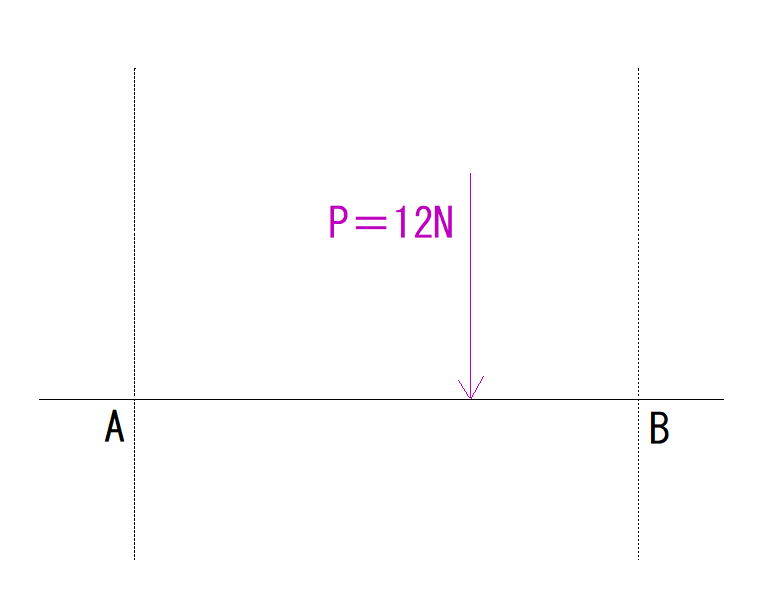
下の図のように力Pが働いたとき、A,Bにはそれぞれどのような力を働かせたら釣合うか、求めなさい。
ただし、力Pの作用線とA,Bにかかる力は平行とします。
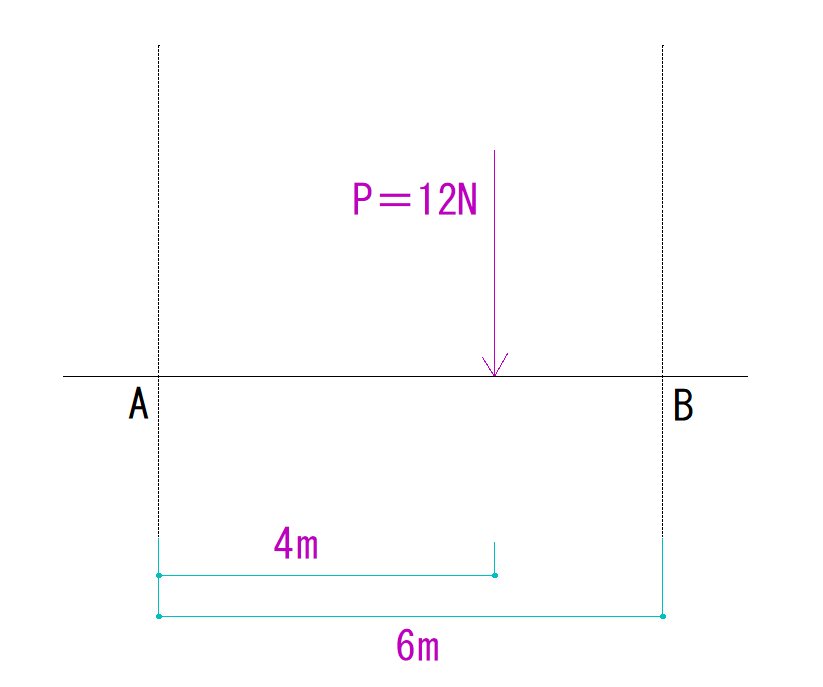
【作用点の違う力の釣合い】算式解法
これを解くには、これまで勉強してきた分野を組み合わせて考える必要があります。
図式解法と考え方は同じです。
まず、力Pに釣合う、ということは、A,Bの合力がPと同じ位置で同じ大きさで逆向きになっている必要があります。


…この図すでに皆さんなら解くことができるはずです!
そうです!
「力を平行に分解」の分野で学びました!
上のリンクからやり方を詳しく知ることができます。
つまり、この合力になるように分力を求めることで、釣合う力を求めることができます。
この合力になるように分解を行う時、ある公式が必要になってきます。
覚えていますか?
そうです、バリニオンの定理です!
バリニオンの定理については下の記事から詳しく見ることができます。
「平行な力の合成の算式解法!バリニオンの定理ってなんなの?」
さて、これ以降はすでに以前取り扱った分野なので、手順はその時の記事を転載しておきます。
【作用点の違う力の釣合い】算式解法 手順
①A(もしくはB)の線上に点Oを決めます。
つまり分力の作用線上に点Oを決めます。
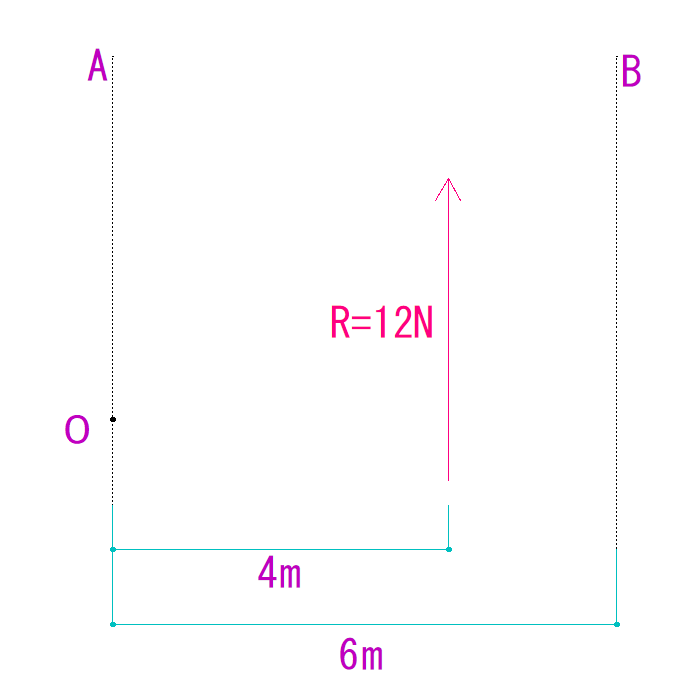
②分力が点Oを回す力を計算します。
…えっ分力の大きさ分からないじゃん?
ってなりますよね。
確かにわからないのでPaをx,Pbをyと置きます。
そうすると…
Paのモーメント力は
x × 0=0 N・m
Pbのモーメント力は
y × 6=6y N・m
点Oを反時計回りに回すので負の符号をつけます。
-6y N・m
それぞれを足してあげます。
0 + (-6y)= -6y N・m
…となります。
③合力が点Oを回す力を計算します。
R=12N
r=4m
12 × 4=48N・m
点Oを反時計回りに回すので負の符号をつけます。
-48N・m
④方程式でyの値を求めます。
バリニオンの定理より点Oを分力が回す力と、合力が回す力が等しくなります。
式で表すと…
-6y = -48
となります。
これを解いていきます。
6y = 48
y = 8 N
となります。
yが何の値だったでしょうか?
yはPbの大きさでした。
よってPbは8N(上向き)です。
⑤xの値を求めます。
合力は分力の和で求めることができます。
つまり
12 = x + 8
よって
4 = x
となります。
xが何の値だったでしょうか?
xはPaの大きさでした。
よってPaは8N(上向き)です。
答えをまとめます。
合力Rの分力、ひいては力Pに釣合う力の大きさは
Paは8N(上向き)
Pbは4N(上向き)
となります。
さて、いかがだったでしょうか?
力の釣合い、という新しい分野に入ったかと思ったら、別に何か新しいことを覚える必要はありませんでした。
ただ、これからの分野は今回のように、以前に習ったことの組み合わせで答えていく必要がある問題が多く出てきます。
ぜひこれまでの基礎の分野を今一度確認しておきましょう!