先回までは平行な力の合成、分解を行っていました。
まだ見ていない方は下のリンクを参照してください。
「平行な力の合成の算式解法!バリニオンの定理ってなんなの?」
「力を平行に分解…えっ意外と面倒くさい?図式解法 算式解法まとめて徹底解説!」
今回の記事について動画でも解説しています。
そちらもご覧ください。
平行でない数力ってそもそも何?
今回は平行でない数力の合成です。
平行ではない数力と言われても難しいですよね。
定義としては、力の作用線が1点に交わらず平行でない力の合成です。
1点で交わる場合の力の合成のやり方は下のリンクを参照ください。
1点で交わらず平行でない…と言葉ではよくわからないと思うので、図を見てみましょう。

見るからに平行でないですしバラバラという感じですね。
バラバラの方向を向いている力を合成する、ということを今回は解説していきます。
これまで合成があれば分解がある、とさんざん言ってきましたが、実はこれは合成することがあっても分解することができません。
なぜできないのでしょうか。
それはいろいろな組み合わせ方ができてしまい、答えが一つに決められないからです。
なので合成方法を覚えてしまえば平行でない力シリーズはおしまいです。
頑張りましょう!
…と気合を入れたところ申し訳ないのですが、実はこの分野は、私が受講していた時はテスト範囲から除外されました。
もしかしたら、授業やテストでやらないという学校もあるかもしれませんが、教科書に一応載っていたので解説したいと思います。
では、例題から考えてみましょう。
【平行でない数力の合成】 例題
下の図の力の合力を書きなさい。

【平行でない数力の合成】解説
平行でない力の合成は平行な力の合成の図式解法とやり方は似ています。
まだ見ておられない方は下のリンクから見ることができます。
使うのは示力図と連力図です。
では、示力図、連力図の書き方を思い出しつつ問題を解いていきましょう。
【平行でない力の合成】解法 手順
①P1を空いている枠に平行移動させます。

②次にP2をP1の矢印の先端につなげるように平行移動させます。

③同じようにP3をP2の矢印の先端につなげるように平行移動させます。

④P1の元からP3の先端を直線でつないだものが合力です。
(ここまで書いてきたものが示力図です)

⑤合力がかかる位置を求めます。
まず示力図の任意の場所に点Oを書き入れます。

⑥点Oからそれぞれの矢印の両端に線(極線)をひきます。
それぞれに番号を振っておきましょう。

⑦極線①をP1と交差するように平行移動させます。

⑧極線②をP1と①の交点を通るように平行移動させます。

ここで重要なのは、どの極線をどこに持ってくるかです。
考え方ですが、示力図で、極線に挟まれている力、そして挟んでいる極線、これら三つが同じ点を通ります。
例えば例題の示力図ではP1が極線①②に挟まれています。
そのためP1と①②が同じ点を通るように平行移動させるのです。


では極線③はどこにもっていくでしょうか?
⑨極線③を②とP2の交点を通るように平行移動させる。
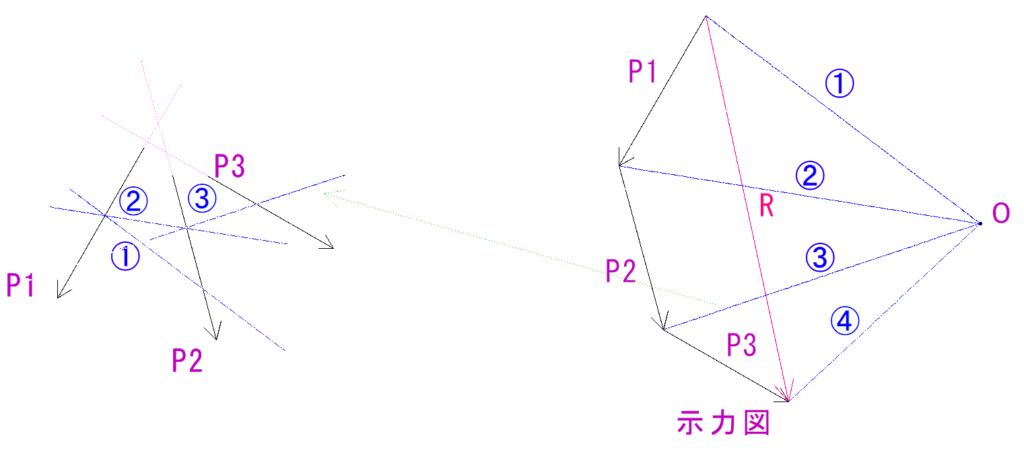
②が短くてP2とぶつかっていない場合は、そのまま延長させて交差するようにしましょう。
極線の長さは示力図で書いた長さ通りでなくて大丈夫です。
⑩極線④を③とP3の交点を通るように平行移動させる。

⑪①と④の交点に、示力図で書いたRを平行移動させる。

ここはなぜ①と④の交点かわかりますか?
示力図を見てください。
Rは極線①と④に挟まれています!
手順8で説明しましたが、示力図で、極線に挟まれている力、そして挟んでいる極線、これら三つが連力図で同じ点を通るように作図します。
よって問題の解答は終了です。
いかがだったでしょうか?
今までに書いた記事で最多の手順11まで行きました。
結構図もごちゃごちゃしてますし、大変だったかもしれないです。
この分野はあまりテストや問題に主立って出てこないので参考程度でいいと思います。 ただ、やり方は平行な力の合成と同じなので、ぜひ理解はしておきましょう。


