さて、前回までは平行な力の合成をしていました。
まだ見ていない方は下のリンクから見ることができます。
「平行な力の合成の算式解法!バリニオンの定理ってなんなの?」
合成があれば分解もあります。
今回は分解方法を解説していきたいと思います。
平行な力の分解…一見簡単そうに思えるでしょうか?
これが意外と難しいです。
…いや面倒くさいという方が正確でしょうか。
覚えてしまえば簡単ですが、手順が多いので覚えるのが大変かもしれません。
でも安心してください。
このサイトでは簡単にわかりやすく説明していきたいと思います。
一気に覚えようとはせず、じっくり時間をかけて覚えていきましょう。
ただ、一つ注意点です。
なんでこの方法で分解できるのか…などと考え始めないようにしましょう。
時間が無くなってしまいます。
これでやればできるんだ!と割り切って考えることをお勧めします。
では、早速下の例題から考えていきましょう。
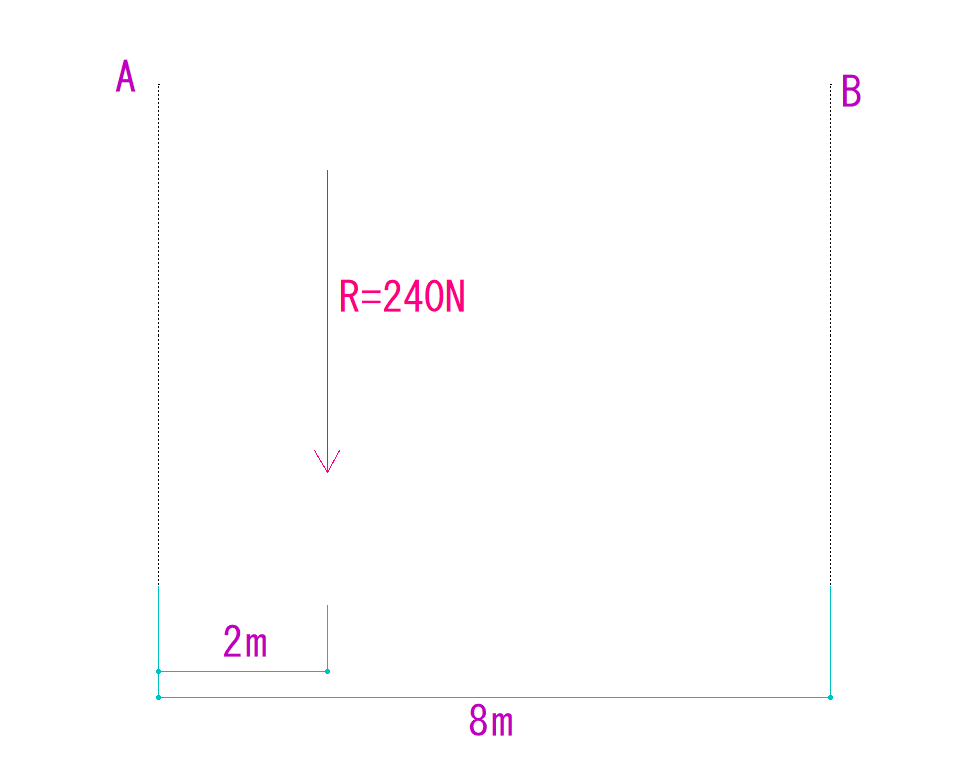
【平行な力の分解】例題
下の図にあるPをそれに平行なA,B上の力に分解しなさい。

【平行な力の分解】作図解法(図式解法)
さて、解法に移っていきましょう。
まず使うものは示力図と連力図です。
示力図の説明は「複数力の合成」
連力図の説明は「平行な力はどうやって合成させる?まずは図式解法を解説!」
にて説明していますのでそちらでご確認ください。
それでは早速説明に移っていきたいと思います。
【平行な力の分解】図式解法 手順
①Pを同じ大きさのまま解答欄の別のところに平行移動し示力図を書きます。
そして任意の場所に点O(極点といいます)を書きます。

②極点から平行移動したRの両端a,bに線(極線)をひき、極線には番号を付けておきましょう。

③極線を問題文に合力のところで交わるように平行移動します。(連力図に書かれる線は連力線といいます)

④連力線と分力の作用線の交点S,Tに直線をひきます。

⑤ ④でひいた連力線を極点を通るように平行移動します。

⑥ ⑤でひいた線とPとの交点をcとします。
ac,cbが分力の大きさです。

⑦連力線①を引いた方に示力図①から出ているacをひきます。
(ここの説明が難しいのですが①の線とAの交点と覚えてもいいかもしれません。
よくわからないようでしたら、先生や教授に説明してもらうのが一番いいと思います。)

⑧逆の方にcbをひきます。

いかがだったでしょうか?
かなり手順が多いですね。
一回で覚えるのは大変かもしれないです。
何回も繰り返し問題を解くことで手順を覚えることができます。
結局こういう問題は経験値がものを言いますので努力しましょう。
【平行な力の分解】計算解法(算式解法)
さて、算式解法に移りたいと思います。
やり方は平行な力の合成方法と同じようなやり方です。
まだ平行な力の合成方法の記事を見られていない方は下のリンクから見ることができます。
「平行な力の合成の算式解法!バリニオンの定理ってなんなの?」
今回も使う公式はバリニオンの定理です。
バリニオンの定理をいま一度確認してみましょう。
バリニオンの定理
「多くの力のある1点に対する力のモーメントは、それらの力の合力のその点に対するモーメントに等しい」
Rr=P1a1+P2a2
すなわちRr=ΣMo
P1,P2…分力の大きさ
a1,a2…それぞれP1,P2の力の作用線とO点との垂直距離
R…合力
r…Rの作用線とO点との垂直距離
ΣMo…各力がO点に対する力のモーメントの総和
この文だけ見てもよくわからないでしょうか。
力の合成の記事にバリニオンの定理について簡単に書かれています。
そちらをご覧ください。
「平行な力の合成の算式解法!バリニオンの定理ってなんなの?」
では、平行な力の分解の算式解法について例題を使って解説していきたいと思います。
【平行な力の分解】算式解法 手順
①A(もしくはB)の線上に点Oを決めます。
つまり分力の作用線上に点Oを決めます。

②分力が点Oを回す力を計算します。
えっ分力の大きさ分からないじゃん?ってなりますよね。
確かにわからないのでPaをx,Pbをyと置きます。
そうすると…
Paのモーメント力は
x × 0=0 N・m
Pbのモーメント力は
y × 6=6y N・m
点Oを反時計回りに回すので負の符号をつけます。
-6y N・m
それぞれを足してあげます。
0 + (-6y)= -6y N・m
…となります。
③合力が点Oを回す力を計算します。
R=12N
r=4m
12 × 4=48N・m
点Oを反時計回りに回すので負の符号をつけます。
-48N・m
④方程式でyの値を求めます。
バリニオンの定理より点Oを分力が回す力と、合力が回す力が等しくなります。
式で表すと…
-6y = -48
となります。
これを解いていきます。
6y = 48
y = 8 N
となります。
yが何の値だったでしょうか?
yはPbの大きさでした。
よってPbは8N(上向き)です。
⑤xの値を求めます。
合力は分力の和で求めることができます。
つまり
12 = x + 8
よって
4 = x
となります。
xが何の値だったでしょうか?
xはPaの大きさでした。
よってPaは4N(上向き)です。
答えをまとめます。
合力Rの分力は
Paは4N(上向き)
Pbは8N(上向き)
となります。
いかがだったでしょうか?
平行な力の合成も分解もバリニオンの定理が重要になります。
公式をしっかりと覚えておきましょう。
また図式解法と同様慣れが必要です。
問題をたくさん解いていきましょう。
解くことでやり方やパターンを理解していくことができます。
宿題
下の図を見て算式解法にて分力Pa,Pbをそれぞれ求めなさい。
答えは次の記事に載っています。
平行な力の合成の算式解法!バリニオンの定理ってなんなの?の宿題の答え
まず2力P1とP2の総和により合力Rの大きさと向きを求めます。
平行で同じ方向に向かっている力なのでここは足し算をしてあげれば大きさは出ますね。
600+400=1000N(下向き)
P1の作用線上に点Oを設け、この点の右の位置に合力Rを仮定します。
そしてO点からの距離をrとしてバリニオンの定理を用いて求めます。
P1は点Oをどれぐらいの力で回すでしょうか?
力のモーメントの公式Mo=Plより
P=600N
l=0m
600×0=0N・m
P2の力のモーメントは
P=400N
l=10m
400×10=4000N・m
P2は点Oを時計回りに回すので正の符号が付きます
よって
4000N・m
それぞれの分力のモーメント力をたしてあげて
0+4000=4000N・m …☆
となります。
次に合力が点Oを回す力を考えます。
合力の大きさは1000Nでした。
よって
R=1000N
l=r
Mo=1000×r
=1000r N・m
Rは点Oを反時計回りに回すので正の符号が付きます
よって
1000r N・m …△
となります。
バリニオンの定理は分力のモーメント力と合力のモーメント力が等しい、(☆の式と△の式が同じ答えになる)という定理です。
式で表すとこうなります。
4000=1000r
4=r
よってrは4mと分かります。
答えをまとめます。
合力Rの大きさは1000N(下向き)でP1の作用線上のO点から右に4mの位置
早足ながら今回も少し丁寧にまとめてみました。
しっかりと復習をしておきましょう。


