今回は力の分解について解説していきたいと思います。
力の分解と聞いて皆さん想像つくでしょうか?
力の合成という考え方をマスターした方なら想像しやすいかもしれません。
(力の合成については前の記事を参照「力の合成 図式解法 算式解法」)
簡単に言えば分解は合成の逆をするということです。
ここで勘のいい方なら気づいたかもしれないですね。
合成にはやり方が大きく分けて2つ、作図方法(図式解法)と計算方法(算式解法)がありました。
分解にも2つ、作図方法(図式解法)と計算方法(算式解法)があります。
また合成の図式解法には力の平行四辺形を利用する場合と力の三角形を利用する場合がありました。
分解にも力の平行四辺形を利用する場合と力の三角形を利用する場合があります。
ちなみにですが、今回の僕のおすすめは力の平行四辺形を利用する場合です。
力の三角形を利用するのは比較的面倒です。
(個人的な意見なので、先生の教え方に従って覚えてください)
さて、具体的にどうやって力の分解をやるのでしょうか?
下の図の問題で一つずつ考えてみましょう。
【力の分解】作図方法(図式解法)
例題

【力の分解】力の平行四辺形を利用する場合
①荷重Pの終点をCとしV軸に平行でC点を通る線を引く。

②U軸と平行でC点を通る線を引く。

③1で引いた線とU軸との交点からO点までの線を引く。

④2で引いた線とV軸との交点からO点までの線を引く

⑤矢印を付けて完了です。

【力の分解】力の三角形を利用する場合
①荷重Pの終点Cを通るV軸に平行な線を引く。

②U軸との交点をAとしOAに線を引く。

③ACに線を引く。

④2で引いた線を平行移動させてV軸に重ねる。

⑤矢印をつけて完成です。

分かりましたでしょうか?
力の分解の時は作用線がもともと問題に出てきています。
それを定規2つ使い平行な線をひいたりして分力を作図します、
問題を解くときやテストの時は定規2つを必ず忘れないようにしましょう。
【力の分解】計算方法(算式解法)
さて次は算式解法について解説していきたいと思います。
算式解法ですが、力の合成と同様、力の作用線が直角の場合についてです。
直角以外のパターンもありますがここでは解説しません。
(直角以外の場合かなり難易度が上がります。学校によっては算式解法自体、授業で触れるだけでテストには出ないというところもあるかもしれません。)
まず、公式がありますのでそれを覚えましょう。
Px=Pcosθ[N,kN]
Py=Psinθ[N,kN]
θ…X軸のなす角度[度]
三角関数が出てきました。
sin,cos,tan…三角関数の分野は苦手な方も多いのではないでしょうか?
直角三角形についての三角関数について下の図にて確認してみましょう。
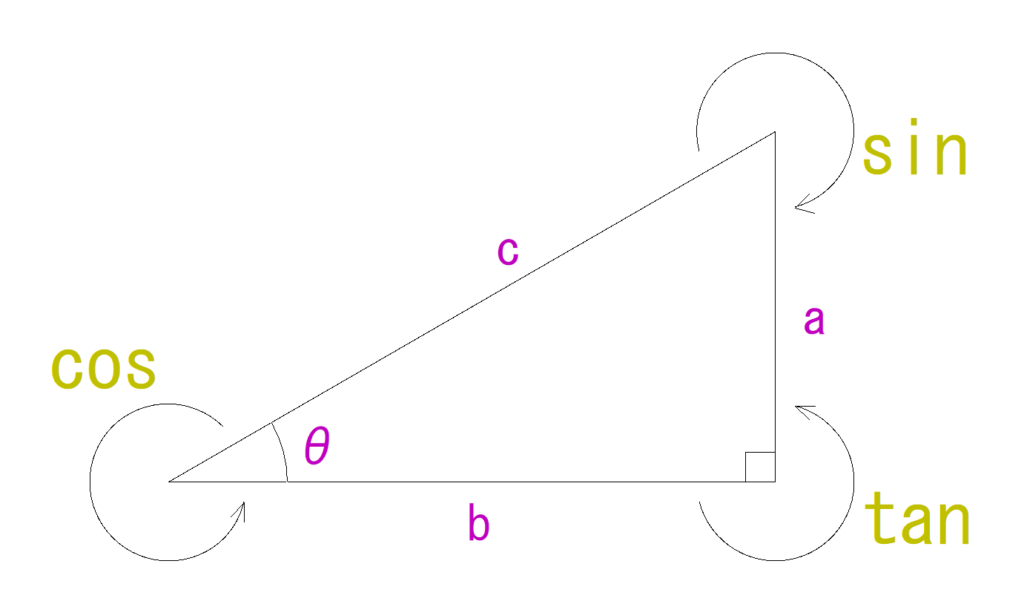

となります。
詳しくは下の記事を参照
…なんだか難しそうですね。
ただここで朗報です!
テストや問題集をやるとわかると思いますが、基本的にθが微妙な角度になることはあまりありません。
例えば60°,30°,45°というのが良く出てくる角度になります。
問題を何回も解くことでパターンが見えてきます。
例題から考えてみましょう。
例題
下の図からX軸、Y軸上の2方向に分解しPx、Pyの値を算式方法で求めよ。
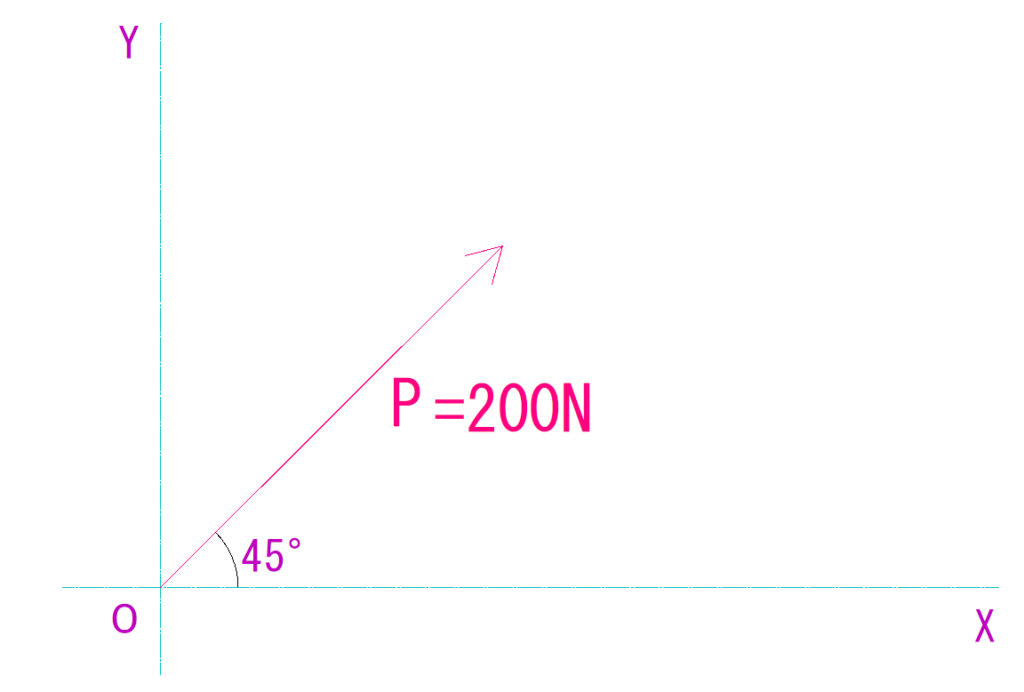
解説
公式にそれぞれ当てはめていきます。


Px=141.4N(右向き)
Py=141.4N(上向き)
これらが答えになります。
数学のような感じになってきましたね…
ただ、関数電卓を使って計算できるので、頭を使うことはほぼありません。
公式、そして三角関数を頭に叩き込んでおきましょう。
注意点
注意点が一つあります。
1向きを忘れない
分力を算式解法で出したときは向きが必要になってきます。
力の後に(○○向き)と書くことが必要です。
忘れないように注意しましょう。
(解説には(有理化する)と書いてありますがそれは解説ですので不要です。)
向きがないと減点対象になる可能性があります。
宿題
下の図より算式解法にてそれぞれの分力の大きさを求めなさい。
答えは次の記事「たくさん力がかかった場合どうするの?複数力の合成をわかりやすく解説!」に書いてあります。

力の合成 図式解法 算式解法の宿題の答え
まず合力を求めます。
公式より

=250000N
次になす角度を求めます。

=1.3
関数電卓を使い、角度を出します。
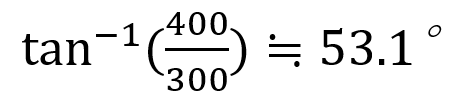
したがってθ=53.1°となります。



