さて、今回からテーマが変わります。
荷重や外力について考えていきましょう。
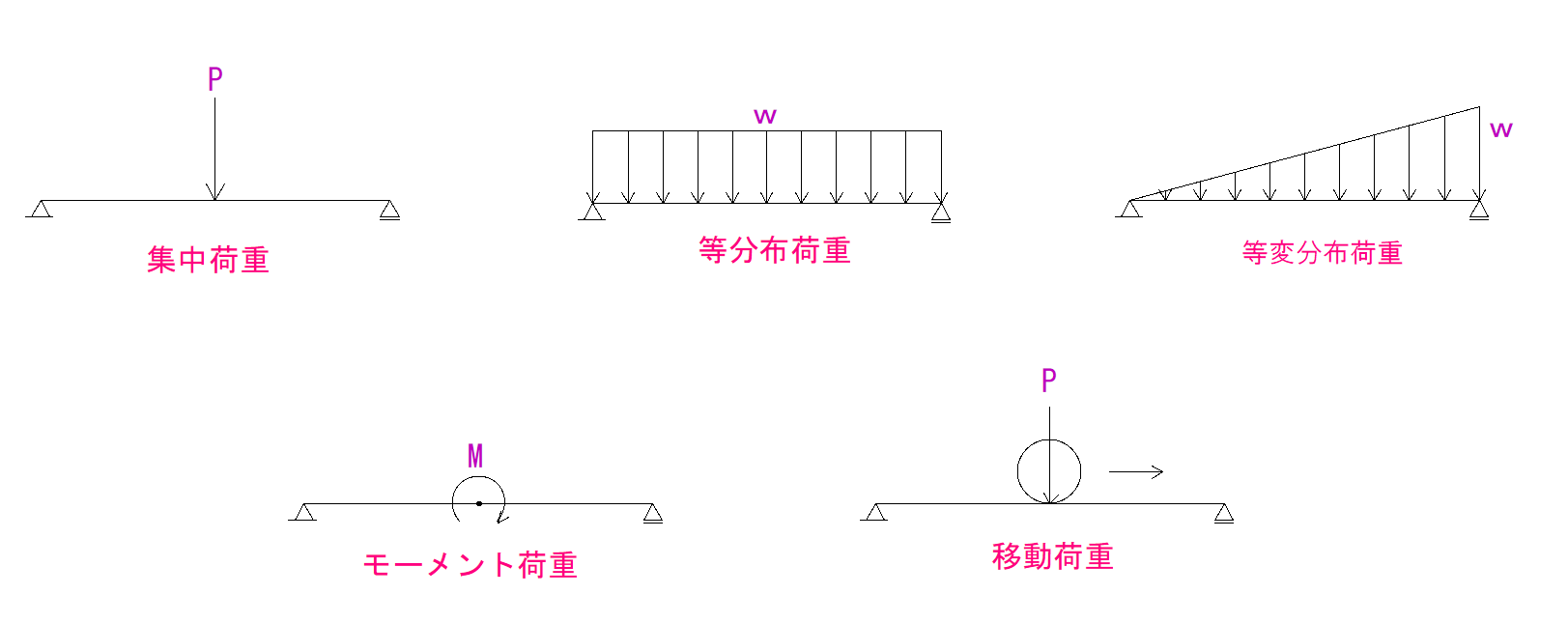
荷重の種類は5つ
荷重には主に5種類あります。
下の図をご覧ください。
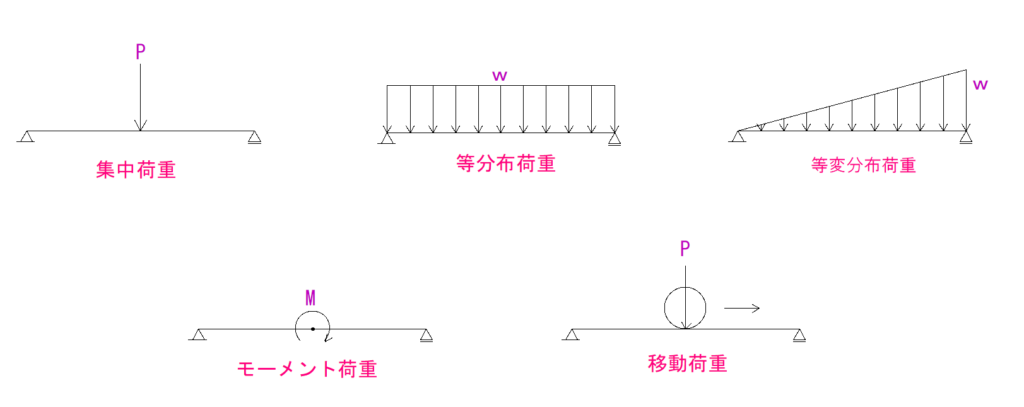
これは暗記分野です。
しっかりと覚えておきましょう。
等分布荷重及び等変分布荷重の合力について
等分布荷重や等変分布荷重はこれまでと少し違うものです。
なぜか、
それは、これまで考えたように1点に荷重がかかるものではないからです。
でもそのままでは面倒くさいので、計算上、合力を求め一つの力として考えることができます。

では、等分布荷重や等変分布荷重の合力はどこにどれぐらいかかるのでしょうか?
詳しくは下のリンクの記事で解説しています。
そちらもご覧ください。
合力の大きさ
実はとても簡単です。
面積を求めればいいんです。
…もう少し詳しく解説しましょう。
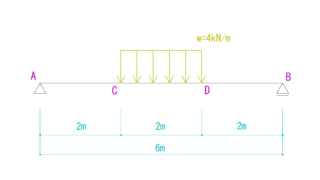
等分布荷重の合力の求め方は、
等分布荷重がかかっているところの距離[l]×等分布荷重の厚さ[w]
となります。
問題の図で確認するとわかりますが、これって面積になっているんですよね。

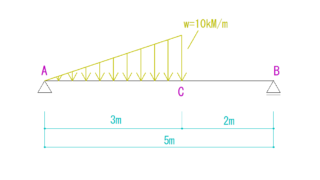
等変分布荷重も同じです。
三角形の面積を求めることで合力の大きさを求めることができます。
等変分布荷重がかかっているところの距離[l]×等変分布荷重の最大厚さ[w] ÷2

合力はどこにかかるか
合力のかかる位置というのは、分布荷重の重心になります。
重心を求める…と聞くとめんどくさそうですが、簡単です。
等分布荷重であれば四角なので真ん中です。
等変分布荷重であれば三角形なので1:2に分けたところとなります。

これは覚えておきましょう。
応用:等分布荷重及び等変分布荷重の合体
ここからは応用編です。
下のリンクの記事でさらに詳しく解説しています。
そちらもご覧ください。
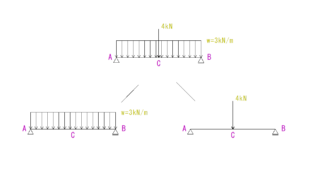
さて、下の図の問題はどうやって解くでしょうか?

これは等分布荷重と等変分布荷重合体系です。
つまり分解してあげれば解決です。

そうしたら、それぞれの合力を求めます。

200×6=1200N
400×6÷2=1200N
次にそれぞれの合力の合力を求めます。
どのようにするでしょうか?
バリニオンの定理を使います。
バリニオンの定理については下のリンクから見ることができます。
「平行な力の合成の算式解法!バリニオンの定理ってなんなの?」

バリニオンの定理により
1200×1=2400×r
0.5=r
となります。
答え

となります。
これから行っていく分野での基礎の基礎になるのでしっかり理解しましょう!