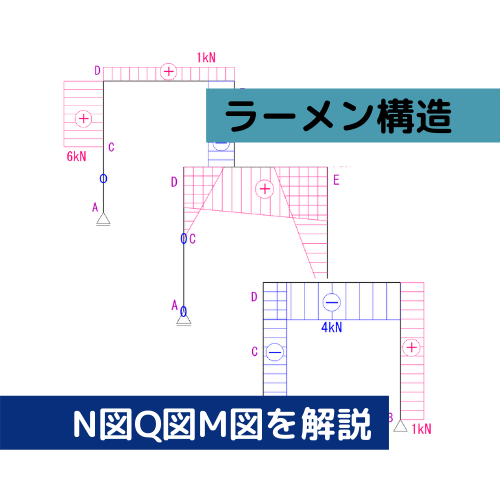
さて今回は単純梁系ラーメンです。
ラーメン構造で一番よく出てくる分野かもしれません。
しっかりと理解しておきましょう。
今回は記事が長いので、目次から知りたいところへ飛んでいただくのがいいかと思います。
この分野を行う前に、まずはN図Q図M図とは何か、単純梁系ラーメンとは何か、また反力の求め方について理解しておかなければなりません。
理解しているか少し不安でしたら下のリンクの記事をご覧ください。
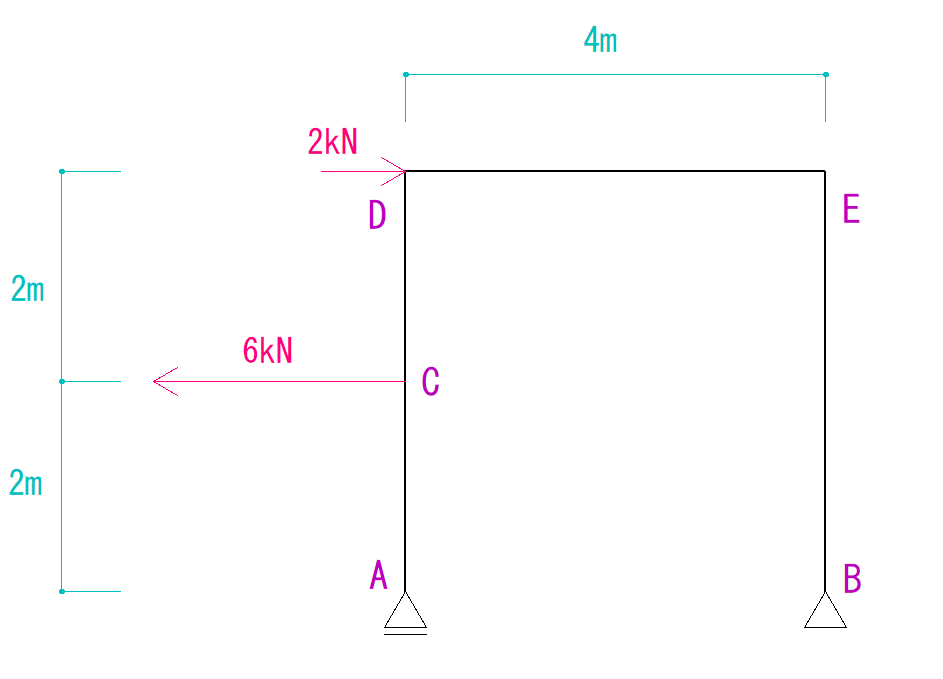
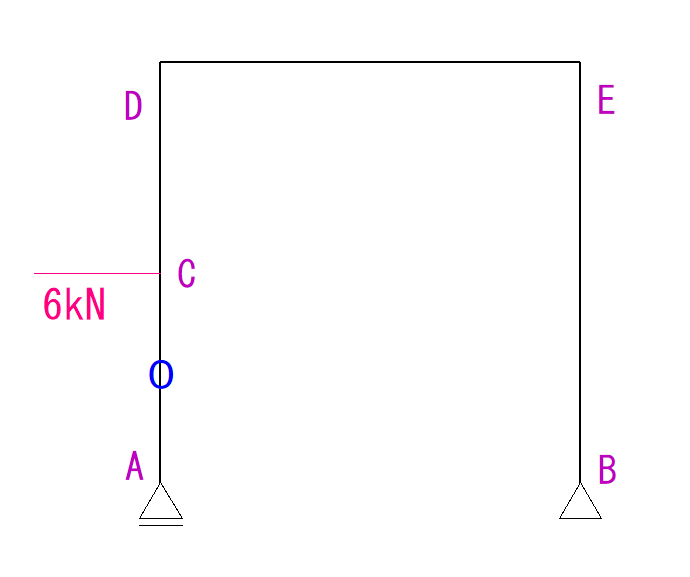
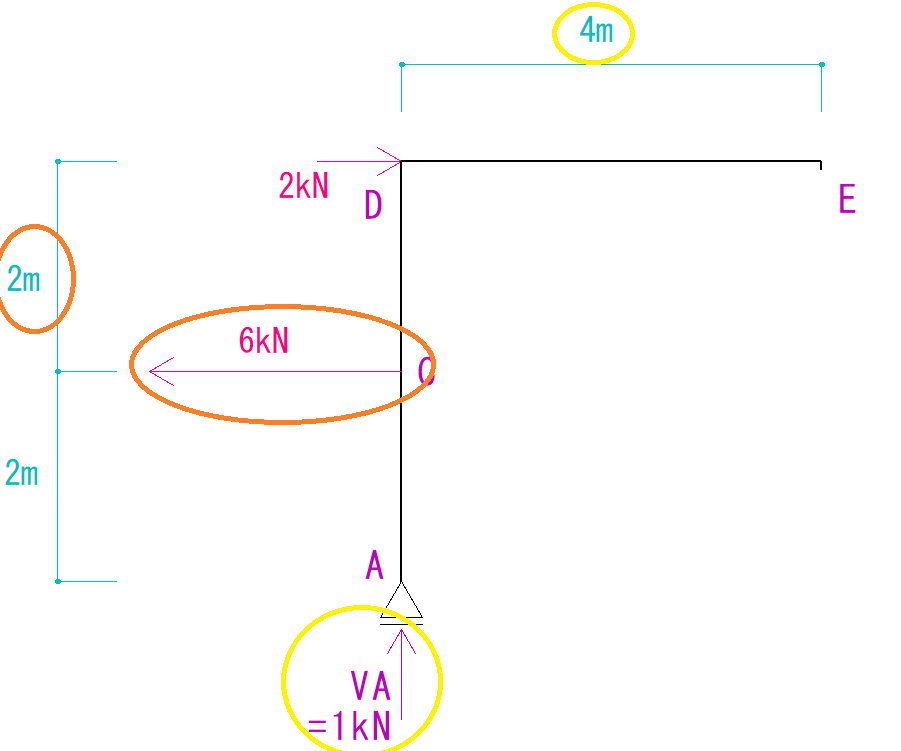
例題
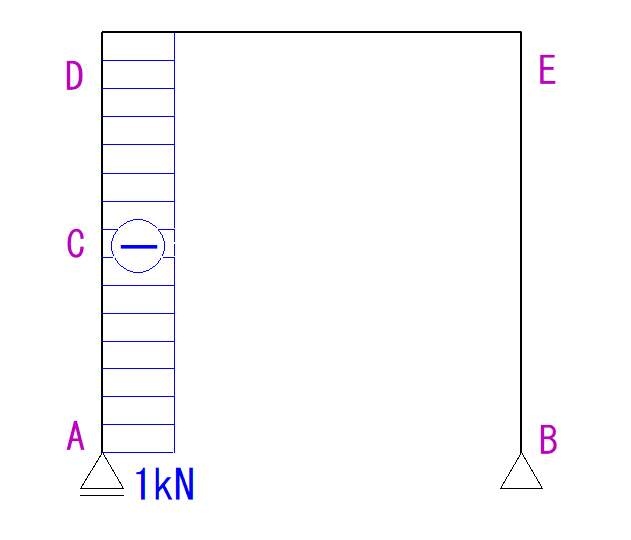
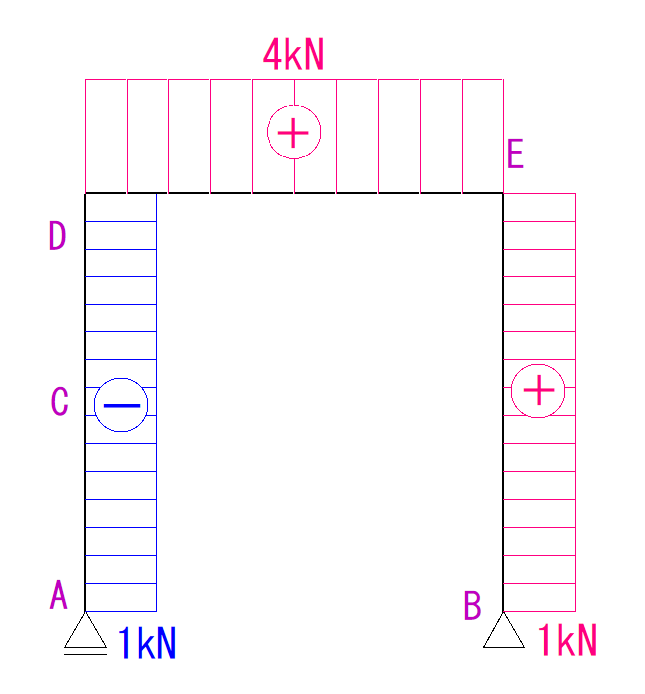
下のラーメン構造のN図Q図M図を描きなさい。
解説
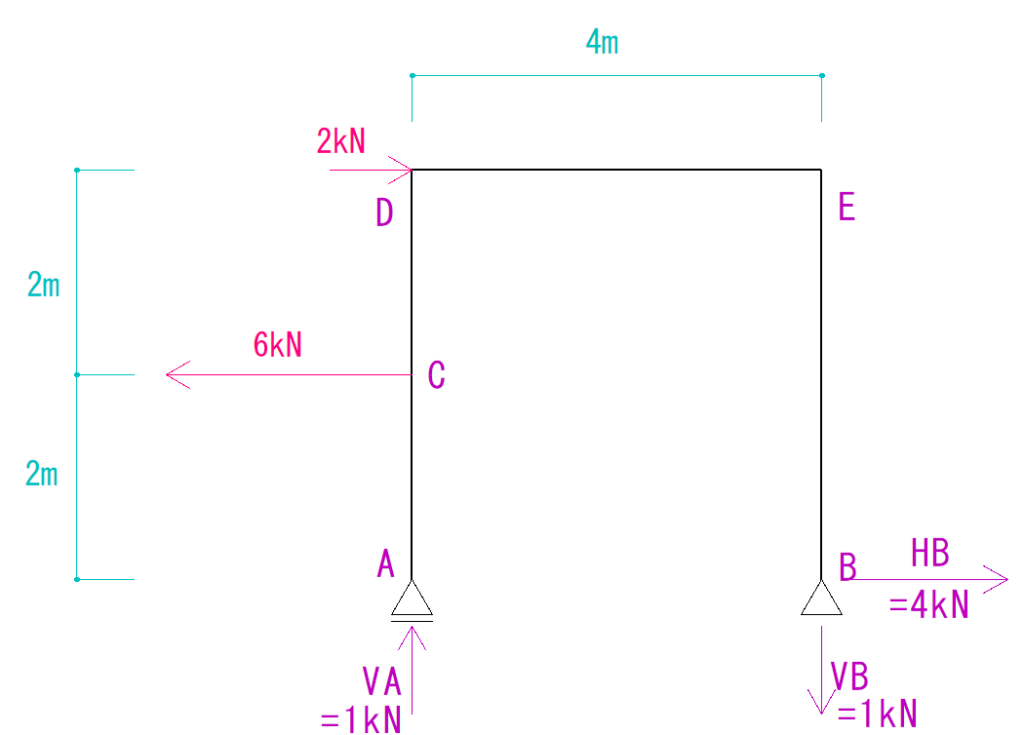
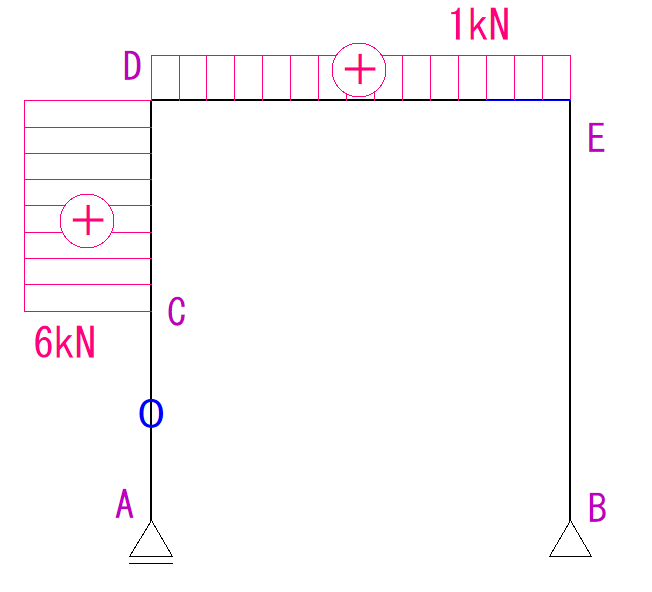
反力を求める
まずは反力を求めなければなりません。
反力の求め方については以前の記事で解説しているのでここでは省略します。
詳しくは下のリンクの記事で解説しています。そちらをご覧ください。
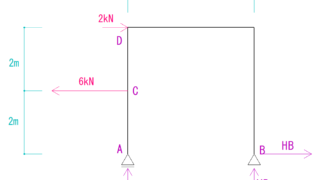
計算すると次のような形になります。
では早速図を描いていきましょう!
N図の描き方
まず、片持梁系ラーメンは軸方向が途中で変わっていることを理解しないといけません。
AD間は垂直方向が軸方向力
DE間は水平方向
EB間は垂直方向です。
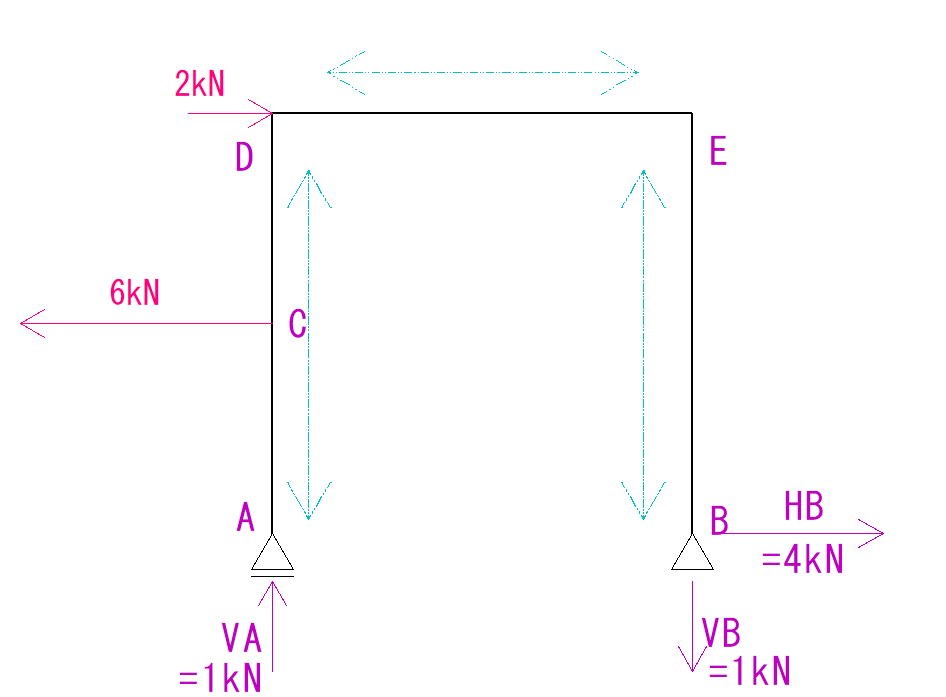
そこでAD,DE,EBの3つに分けて考える必要があります。
ADの軸方向力
ADだけを見てみましょう。
ADには反力のVAが部材を下から押すような力としてかかっています。
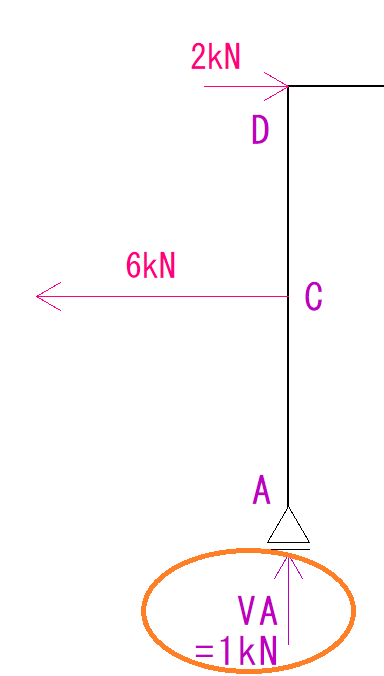
つまり軸方向力は反力の分かかっているのです。
大きさは1kNとなります。
符号ですが、部材を押す場合どちらになるでしょうか?
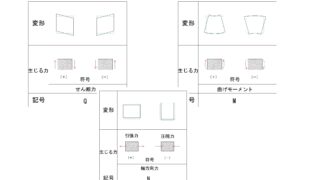
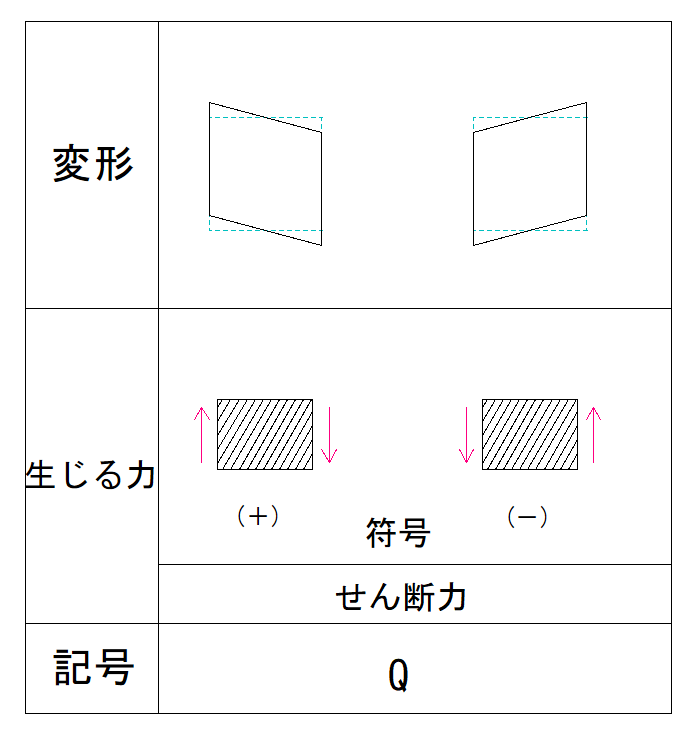
下の表を見て確認してみましょう。
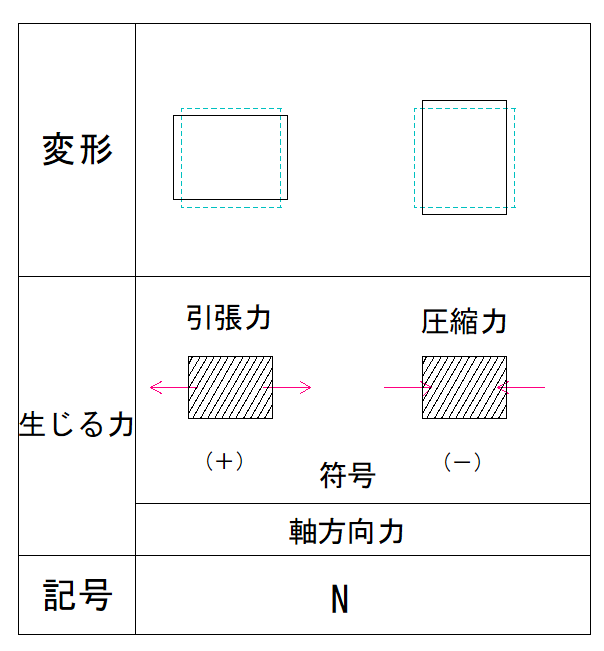
部材を押し込む、つまり圧縮する力なので符号はマイナスとなります。
参考
ラーメン構造のN図Q図の符号
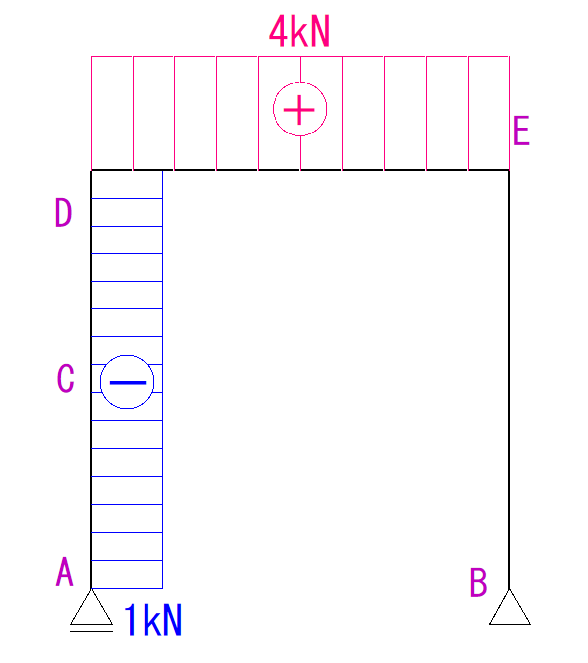
AD間ではそれ以外に軸方向力はかかっていないのでN図は下のようになります。
DEの軸方向力
次はDEだけを見てみましょう。
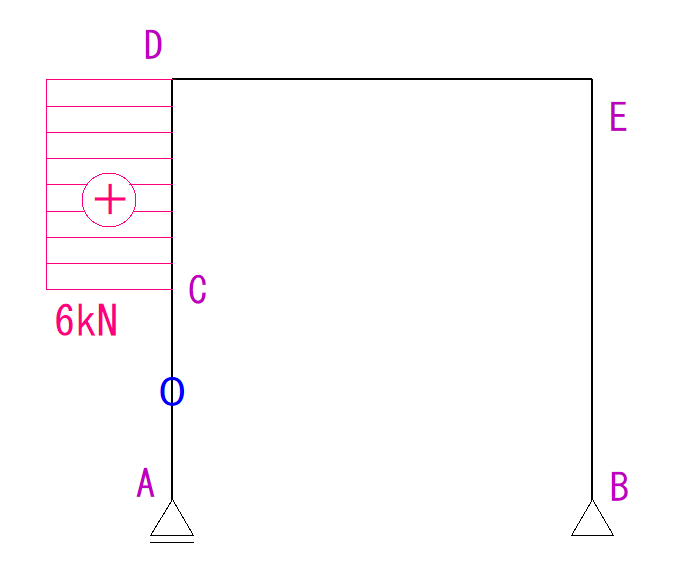
DEだけを見ると荷重の2kNしか、かかっていないように見えるかもしれません。
しかし、少し視野を広げると6kNの荷重と反力のHB4kNがDEの軸方向の力として存在しています。
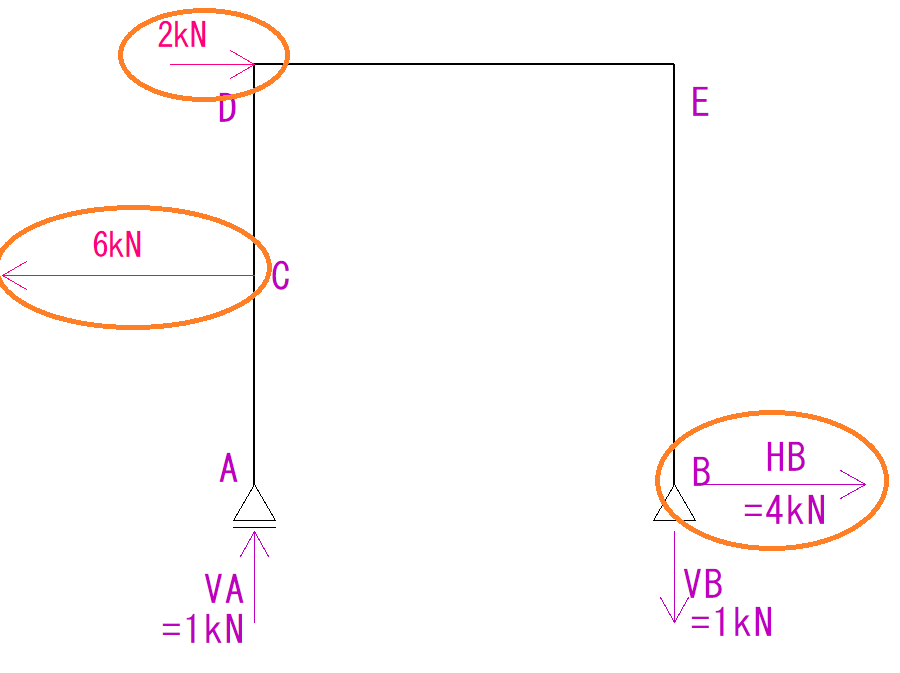
重要な点ですが、ラーメン構造では直接部材に力が加わっていなくても、力は部材内を移動するという特質を持っています。
ラーメン構造では力が部材内を移動している
つまりDEには実質、下のような力が加わっているということができます。
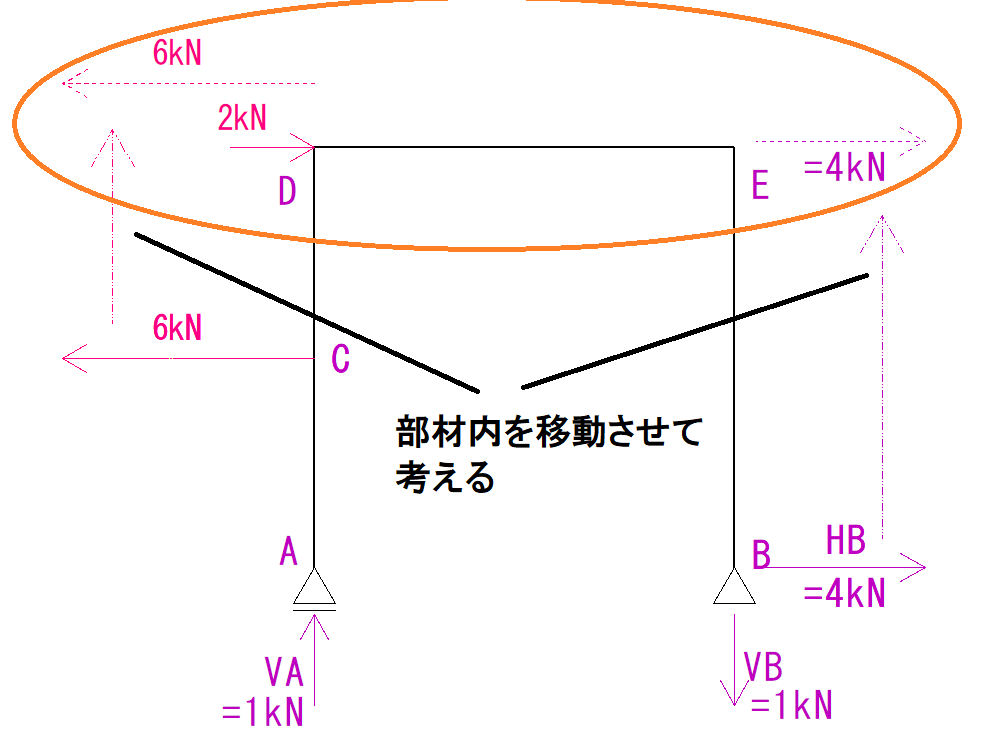
荷重は打ち消しあう力なのできれいにしてあげます。
そうするとこのようになります。

あとはN図を描いていきましょう。
大きさはDE間で変化していないのでそのまま4kNとなります。
符号はどうなるでしょうか?
下の表を確認してみましょう。

引張り力がかかっているので符号はプラスとなります。
N図に描き込みます。
EBの軸方向力
最後にEBだけを見てみます。
これはAD間を考えた時とほぼ同じなので詳しくは説明しません。
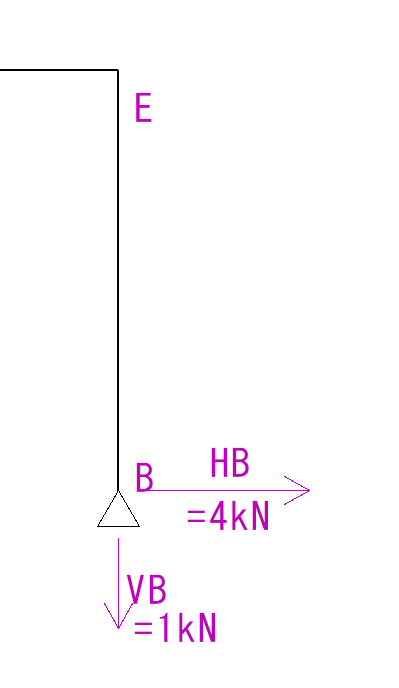
ADにかかる軸方向力は反力の1kNのみなので、そのまま大きさは1kNとなります。
符号はどうでしょうか?
今回も引っ張り力です。
下の表から確認してみましょう。

引っ張り力は符号がプラスになります。
よってN図は下のようになります。
これでN図は完成です!
Q図の描き方
大体のやり方はN図と同様です。
AD,DE,EBに分けて考えます。
ADのせん断力
ADは荷重がせん断するようにかかっています。
B点の反力も部材内を移動して力をかけているので、イメージとしてはこのようになります。
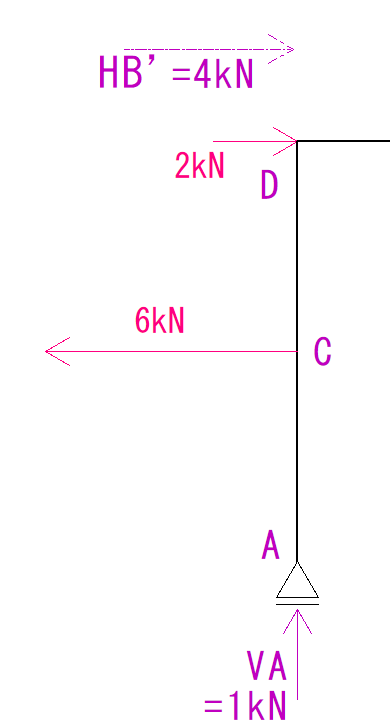
こうしたら後はいつも通りQ図を描いていきましょう。
AからC間はせん断力がかかっていません。
よって0になります。
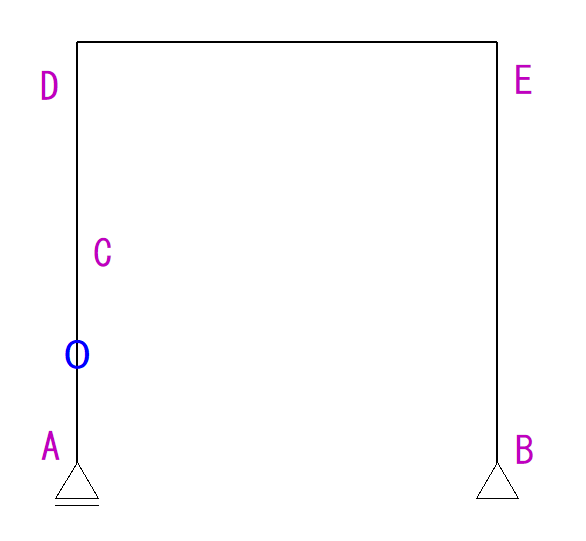
C点で荷重が左向きにかかっているので荷重の大きさ分だけ左に出します。
符号はプラスとなります。
参考

ラーメン構造のN図Q図の符号
符号のイメージ
D点で荷重と反力の和の分右に下がります。
式:6kN+(-2kN)+(-4kN)=0kN
DEのせん断力
DEは一見せん断する力がないように見えます。
しかし、視野を広げると反力があります。

これらがDEをせん断するように力をかけているので、イメージとして下の図のように考えることができます。

これは簡単ですね。
途中でせん断力の変化もないので符号を確認して描いていきましょう。
大きさはそのまま1kNです。
符号は表で確認しましょう。

表を見てわかるように今回はプラスです。
Q図は下のようになります。
EBのせん断力
EBはADと同様です。
荷重は部材内を移動してかかっているので、荷重分がE点にかかります。
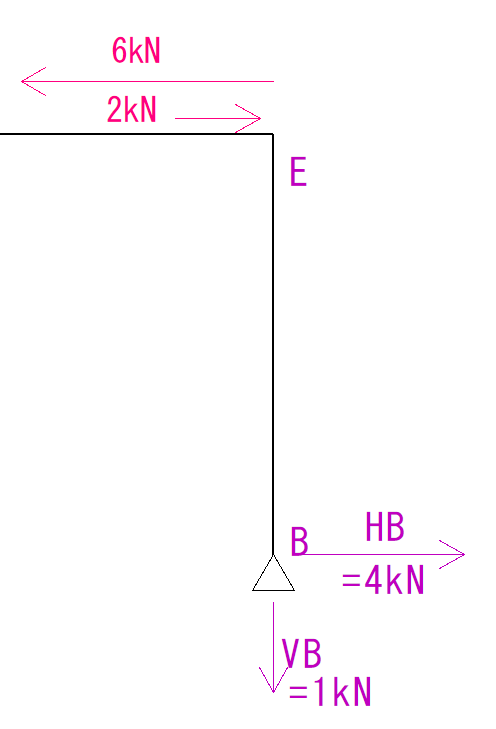
後はQ図を描くだけです。
部材内でせん断力は変化していないので、符号を確認してすぐに描くことができます。

表より符号はマイナスです。
大きさはそのまま4kNなので図は下のようになります。
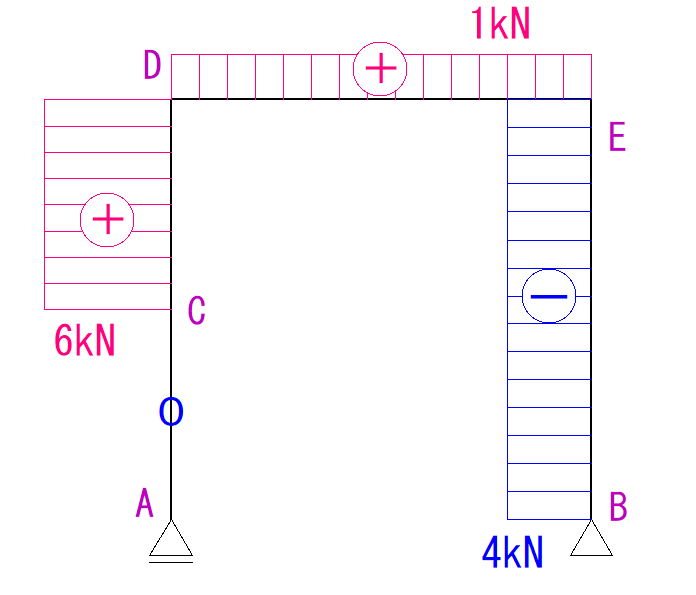
これでQ図は完成です!
M図の描き方
M図の場合はやり方が少し変わります。
A点C点D点E点B点のそれぞれのモーメント力を調べ、それを線でつなぎます。
いっぱいあって大変だ!と思うかもしれませんが、意外と簡単です。
なぜなら、支点となるA点B点はモーメント反力がかかっていないため、モーメント力は0になります。
よって計算するのはC,D,Eの3つだけです。
早速やっていきましょう。
では、まずはC点から考えていきましょう。
モーメント力は端から見ていくのがセオリーです。
そうすると、C点には回転させる力がかかっていないことが分かります。
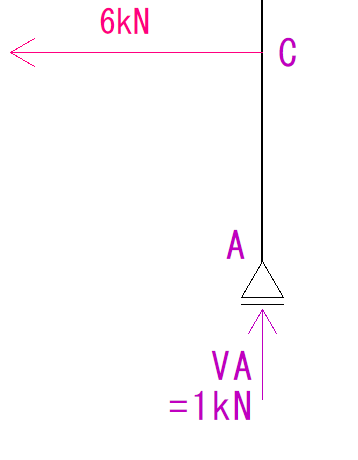
(2つの力とも、力の作用線とC点が重なり、距離が0なのでモーメント力も0になります。)
次にD点です。
D点はC点にかかる荷重がモーメント力をかけています。
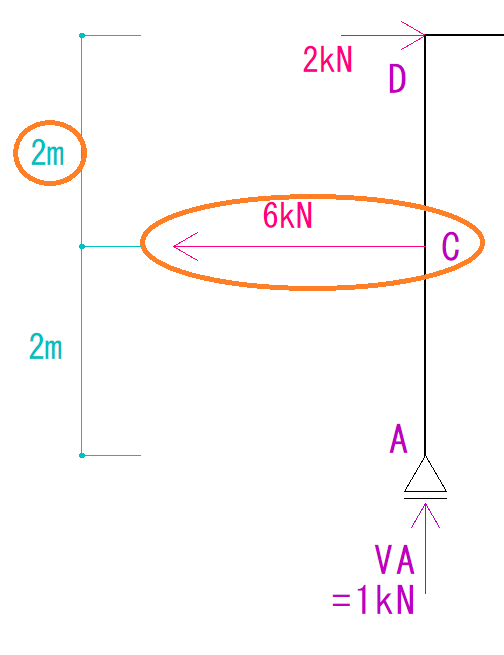
大きさは
6kN×2m=12kN・m
となります。
符号はプラスとなります。
参考
ラーメン構造のM図の符号
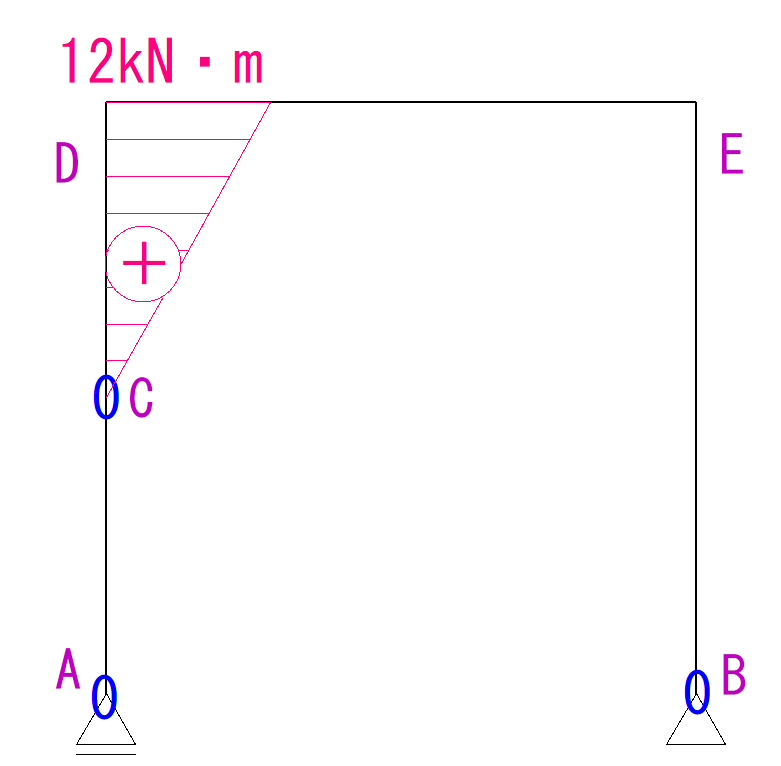
最後にE点です。
E点を回す力はC点にかかる荷重、そしてA点にかかる反力となります。
これらを計算して足しましょう。
6kN×2m+1kN×4m=16kN・m
となります。
符号はプラスとなります。
あとはそれぞれの線を繋ぎます。
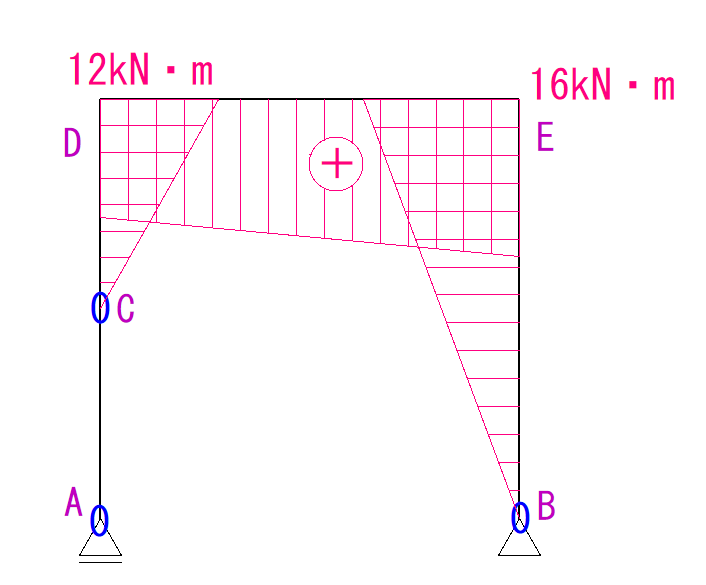
符号と大きさをしっかりと書き入れましょう。
これで完成です!
まとめ
お疲れさまでした。
少し長く大変だったのではないでしょうか?
この記事を書くにあたり、ややこしくならないように解説を省いてしまったところもあります。
(符号の確認の仕方など…)
もしわからないところがある方は、ぜひお気軽にTwitterなどでご質問ください!