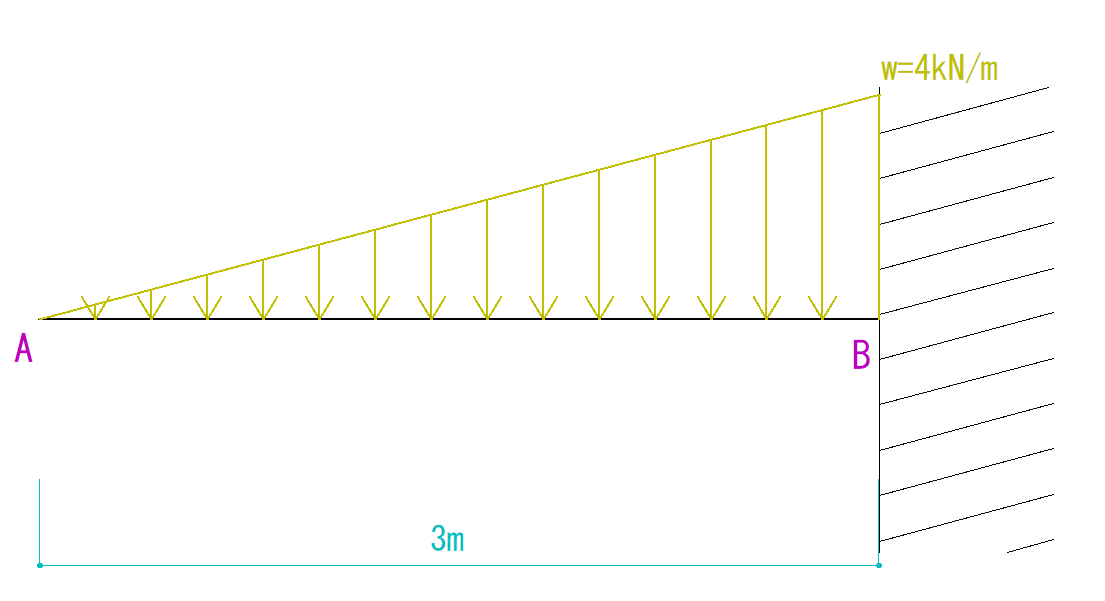
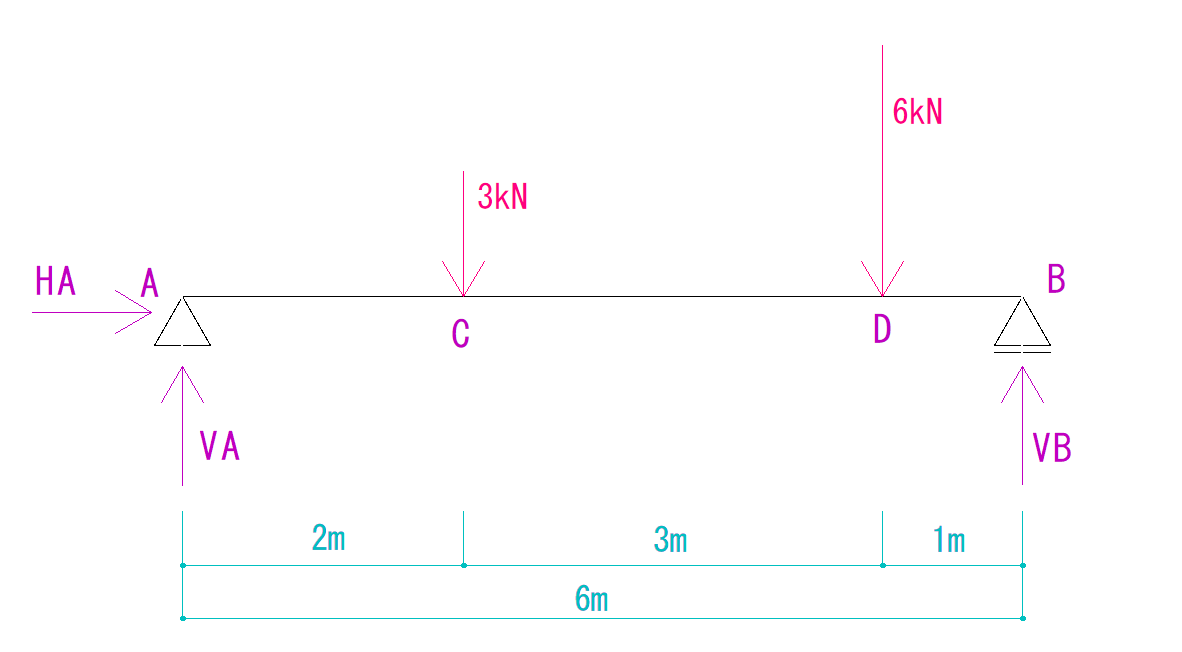
当サイトではTwitterで質問できる「質問コーナー」というものをやっているのですが、そこから寄せられた質問の傾向から、少し戻って飛ばした分野、「反力の求め方」シリーズを行っていきたいと思います。
(質問コーナーについては下のリンクを参照)

ということで、今回は単純梁に集中荷重がかかった場合の反力の求め方を解説していきます。
例題
下の図を見て、反力を求めなさい。
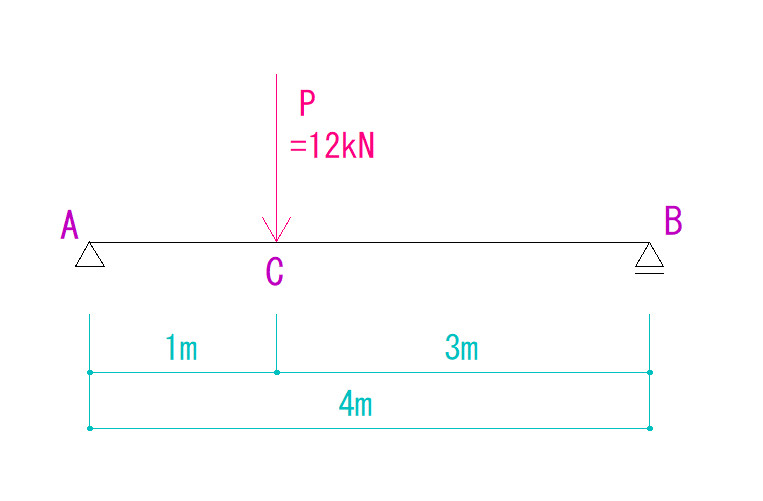
解説
反力の仮定
まず、それぞれの支点にどの種類の反力が、いくつかかるかを確認します。
これについては下のリンクの記事を参照ください。
この場合は下のように反力を仮定することができます。
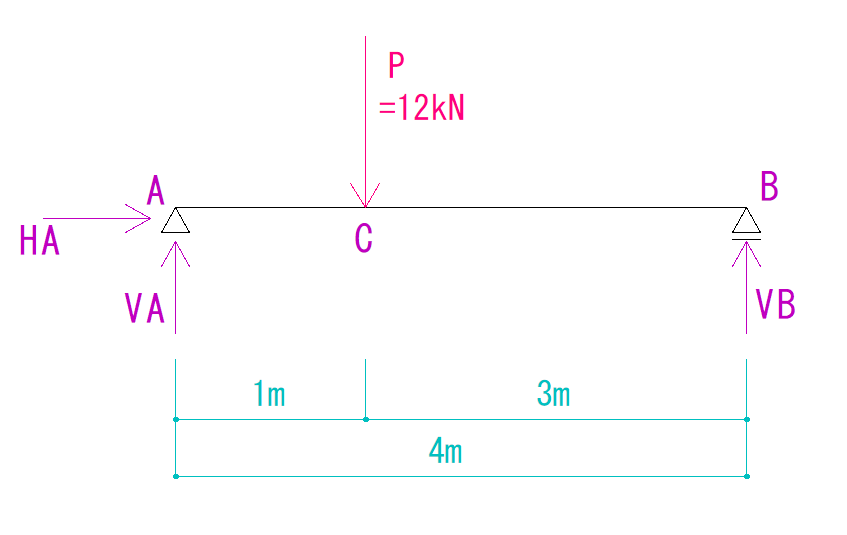
注意ですが、この時、反力の符号がプラス向きにするようにすることをおすすめします。
補足:力の符号について
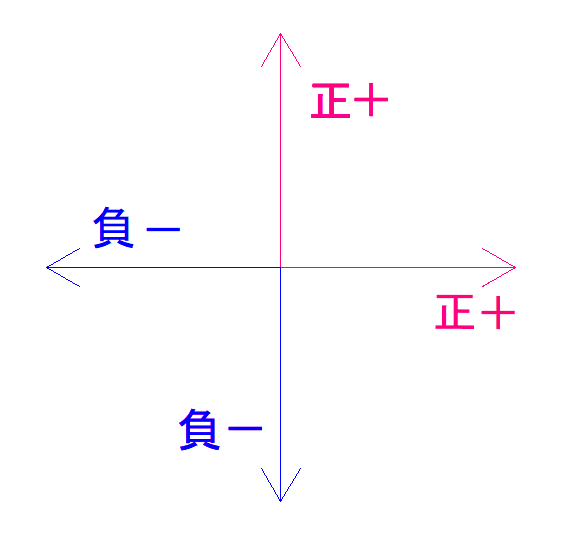
そうすると、これから式を立てるとき符号ミスが減ります。
(明らかにマイナスの向きにかかる場合は、仮定でマイナス向きにしてもいいですが、符号は間違えないようにしましょう。)
では、問題を解いていきます。
釣合い条件から計算
「反力を求める」
というのは言い換えれば
「問題の力に釣合う力を求める」
ということです。
そこで力の釣合い条件を思い出してみましょう。
ΣX=0
ΣY=0
ΣRM=0
です。
これらの条件から、反力を求めていきます。
ΣX=0
X方向にかかっている力に注目します。
今回の問題では HA だけしかありません。
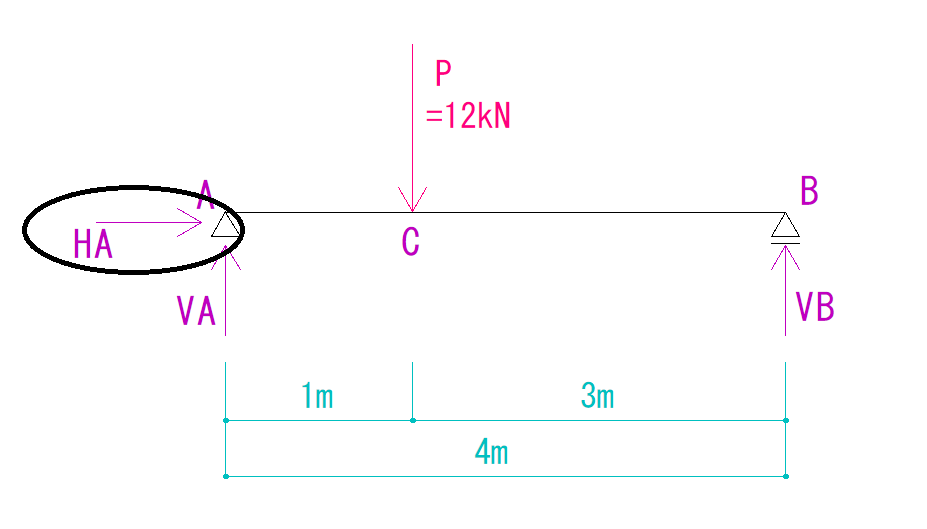
式に当てはめると、
HA=0
となります。
そのため、HAの答えはこのまま、
HA=0kN
となります。
ΣY=0
Y方向にかかっている力に注目すると、3つあることが分かります。
VA VB P(12kN)
の3つです。
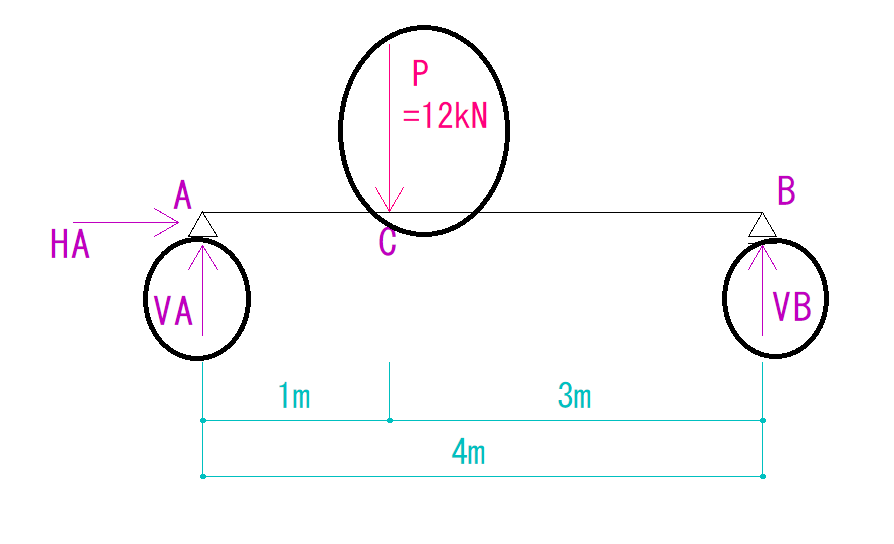
それぞれを式に当てはめていきます。
VA+VB+(-12kN)=0 …☆
Pは下向き、つまりマイナス方向に力をかけているので、符号もマイナスを付けます。
これ以上計算できないので、とりあえずこのままにします。
ΣRM=0
これはどこに点を取っても、すべての力のモーメント力の和がゼロになるという意味です。
言葉ではうまく伝わらないかもしれないので、問題を解きながら考えていきましょう。
今回はO点をA点に仮定します。(どこに点を取っても大丈夫です)
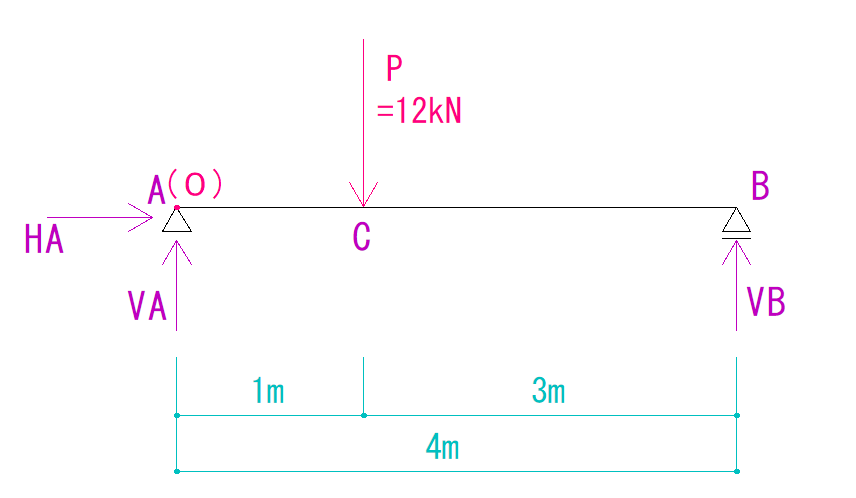
そこから、それぞれの力がA点(O点)を回す力の計算をしていきます。
VAがA点を回す力
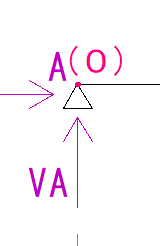
VAはA点との距離が0なので、モーメント力も0になります。
HAがA点を回す力
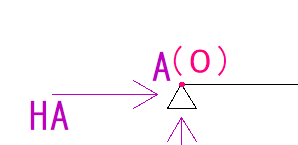
HAもVAと同様に、A点との距離が0なので、モーメント力も0になります。
P(12kN)がA点を回す力
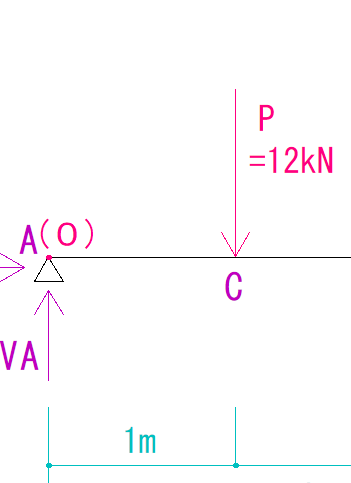
モーメントの公式より、PがA点を回す力は
12kN × 1m = 12kN・m
PはA点を時計回りに回すので符号はプラス
+12kN・m
となります。
VBがA点を回す力
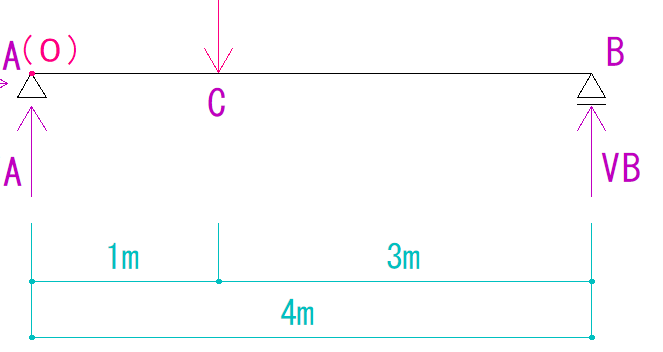
モーメントの公式より、VBがA点を回す力は
VB × 4m = 4VB kN・m
VBはA点を反時計回りに回すので符号はマイナス
-4VB kN・m
となります。
ΣRM=0の釣合い条件に当てはめる
ΣRM=0の式に当てはめると、
0 + 0 + 12 kN・m +(-4VB kN・m) =0
12 - 4VB = 0
12 = 4VB
VB = 3kN
となります。
答えがプラスだったので、仮定の向きで合っていたことが分かります。
代入していく
VBが分かったら先程の☆マークの式に代入してVAを求めます。
VA+VB+(-12kN)=0 …☆より
VA+3kN+(-12kN)=0
VA+(-9kN)=0
VA=9kN
となります。
こちらも、答えがプラスだったので、仮定の向きで合っていたことが分かります。
答え
答をまとめるとこうなります。
HA=0
VA=9kN(上向き)
VB=3kN(上向き)
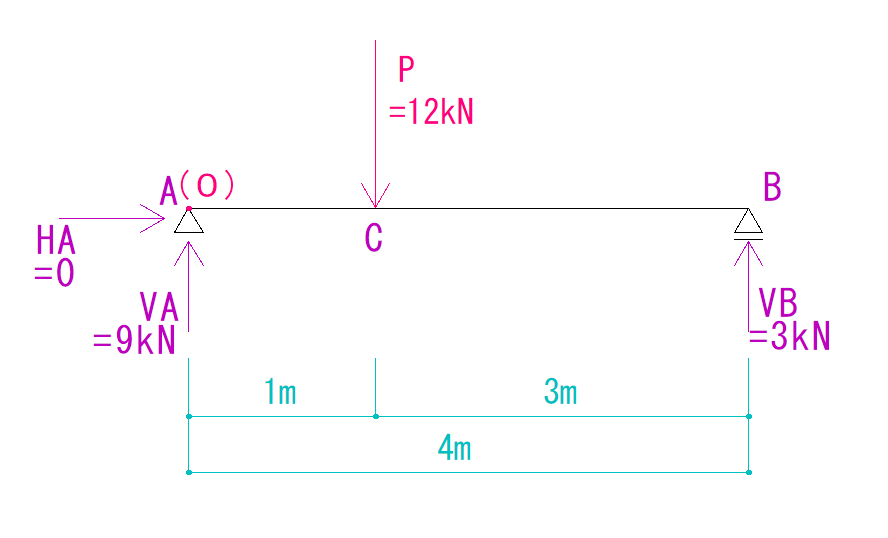
しっかりと力の向きも答えましょう。
これで終了です。
まとめ
建築構造設計で最初に倣う分野の一つです。
基礎の基礎なので、しっかりと覚えていきましょう!