さて、今回は力の釣り合い(力の釣合い)という分野を理解していきたいと思います。
ここからの分野は徐々に複雑になっていくかと思います。
このサイトでは丁寧に解説していきたいと思いますので、一回で覚えようとせず徐々に理解していってください。
力の釣合いって何なの?身近な例で考えてみよう!
まずは力のつり合いという言葉の意味を理解しましょう。
「釣合い」という言葉は日常生活でもよく耳にしますね。
例えば
「俺なんかあんな美人とは釣合わない…」
とか聞いたら意味を理解することはできると思います。
…なんか悲しい例えができてしまいましたが、簡単に言うと「釣合う」とは、バランスが取れている状態のことです。
つまり「力が釣合っている」とは力同士がバランスをとっている状態のことを指します。
力同士がバランスをとっているとはどういう状況でしょうか?
大勢で綱引きをしているところを想像してみてください。

みんな頑張って引いていますが、相手も引いていて、綱の真ん中は動いていません。
これが、力が釣合っている状態です。
自分たちが引いている力と相手が引いている力がバランスをとっている、つまり力が釣合っています。
まとめると、力が釣合っている状態とは、複数の力が物にかかっているにもかかわらず、動いていない状態のことです。
建物の躯体(柱や梁など)はいろいろな力がかかっているにもかかわらず、ピクリとも動かず建物を支えています。
これは力が釣合っているからです。
身近に力の釣合いがある、と思うと少し親近感わきませんか?
では、力が釣合っているかどうかというのは、どうやって確かめることができるでしょうか?
力が釣合うには条件があります。
図式解法での釣合い条件、算式解法での釣合い条件それぞれを見ていきましょう。
ここでは1点に働く力の釣合いについて考えていきます。
【力の釣合い】図式解法
図式解法による力の釣合い条件
図式解法での釣合い条件は簡単です。
示力図が閉じていること、だけです。
…示力図ってなんだっけ、と思う方がいるかもしれないので、もう少し簡単に説明したいと思います。
問題に出てくる力の矢印を順番につなげていって、最終的に最初の点に戻ってきたら、力が釣合っているといえます。
言葉では少し難しいので下の図を見てください。

このように力が釣合っているときの示力図を、示力図が閉じている、と言います。
【力の釣合い】算式解法
算式解法による力の釣合い条件
算式解法を考える前に、少し前提となる話をしたいと思います。
それは
「全ての力はX軸とY軸に分解できる」
ということです。
何言っているんだって感じでしょうか?
下の図を見てみてください。

このようにどんな力もX軸とY軸に分解できます。
なんでわざわざ分解するかというと、釣合っているかどうかを確認するためです。
下の図のように、向きが反対方向で大きさが同じだとわかっているなら、わざわざ分解して比べる必要はありません。

しかし、そんなに都合のいい問題は出ません。
向きや大きさがバラバラの力同士が釣合っているのかどうか比べる場合、まずは全部の力をX軸とY軸に分解し、それぞれを比べる必要があります。
そこで算式解法の力の釣合い条件ですが、
「ΣX=0かつ
ΣY=0」
です。
X軸に分解した力を足していって0になり、同じようにY軸に分解した力を足していったものが0になった時、力は釣合っているといえます。
例題から少し考えてみましょう。
【力の釣合い】例題
下の図のような力が物体に働いています。
これらの力が釣合っているときPxとPyにはどれぐらい力がかかるか求めなさい。

【力の釣合い】算式解法 解説
これを解くにはまず、基本的な三角形の比率を覚えていなければいけません。
問題をいま一度見てみましょう。
問題のまま見ると、どこにも三角形はありませんが、斜めだった力を分解すると…

直角三角形が出てきました!
しかも基本的な三角形です。
では手順をまとめましょう。
【力の釣合い】算式解法 手順
①数値が分かっている力を分解する
釣合っているという条件なので、分解したPx´とPy´はそれぞれPxとPyの大きさと等しいことが分かります。
よってPx´とPy´を計算で出すことでPxとPyを求めることができます。
②先ほど見た図のように少し変形させると三角形ができることが分かります。
そうしたら三角比を用いてそれぞれの力を求めていきます。
(基本的に三角比は基本的な三角形しか出てきません。なので暗算でも計算していくことができます)


つまり、

となります。
頭のいい方はもう暗算で行けると思いますが、今回は丁寧に解説したいと思います。
まず3つ連なっているためによくわからないという方もいるかもしれません。
なので一つずつバラして考えてみましょう。
まず、
Px´:500=1:2の部分です。
ここは簡単ですね。
これはPx´を1としたとき、500は2だよ、という意味です。
もう少しわかりやすく考えるとPx´の2倍は500だよ、という意味です。
Px´×2=500
Px´=250
となります。
次はルートが出てきて面倒くさそうですが、実は簡単に考えることができます。

ここの部分を抜き出します。
Px´は250Nと分かっているので、

となります。
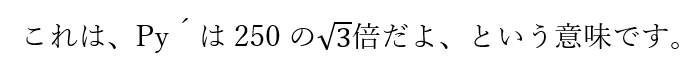
よって
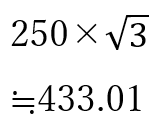
Py´は433Nと出すことができます。
答え
答えをまとめます。
最初にも言いましたが、この問題は釣合っているという条件なので、分解したPx´とPy´はそれぞれPxとPyの大きさと等しいことが分かります。
よって、
Px=250N
Py=433N
となります。
釣り合いの分野でのテストでの出題傾向としては、図を見せてこれは釣合っているかどうかを確認させるタイプと、今回のように釣合っている場合個々の大きさを求めよタイプ、の二パターンあります。
ぜひどっちもできるように理解を深めておきましょう。



