さて、単純梁のQ図M図シリーズ最後の分野となりました。
今回は単純梁にモーメント荷重がかかった場合の、Q(せん断力)図M(曲げモーメント)図の描き方を解説していきたいと思います。
先回までは計算づくめで大変だったかと思いますが、今回は比較的簡単です!
まずは、モーメント荷重についてですが、それが何かわからないと先に進めません。
復習しておきたい方は下のリンクから見ることができます。
例題
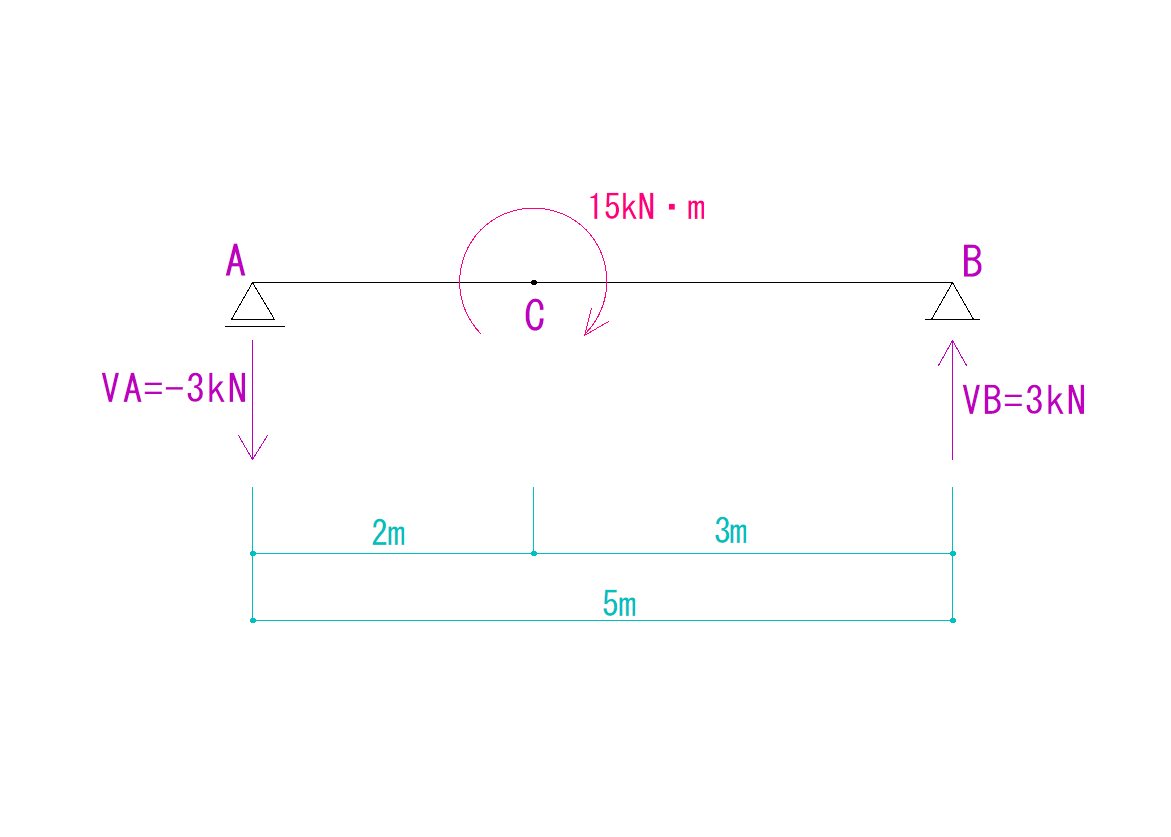
下の図を見てQ図M図を求めなさい。
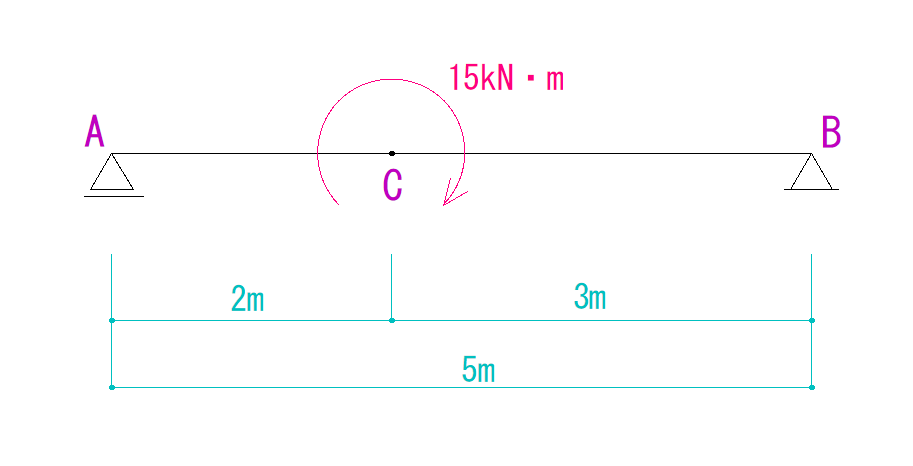
解説
反力の仮定
まずは反力を仮定し、求めていきます。
この問題では水平力が働いていないため、水平反力及びN図は省略します。
さて、実はこの問題鉛直方向にも力が働いていません。
…ということは鉛直反力も0?
…ではありません。
反力0だと、このモーメント荷重(物を回す力)によって、単純梁がぐるぐる回ってしまいます。
このモーメントは止めないといけません。
では、どうするのか。
実はすでに習った分野で解くことができます。
それは…
「偶力」
です!
覚えているでしょうか?
忘れてしまった方は下のリンクから記事を見ることができます。

この問題では、モーメント荷重が時計回りに15kN・mの力で回しています。
これを止めるには、偶力を使い、反時計回りに15kN・mの力を加えないといけません。
それでは、偶力の公式に当てはめます。
偶力の公式は下の物です。
M=PL[N・m,kN・mなど]
P…一方の力の大きさ[N,kNなど]
L…2力間の垂直距離[mm,mなど]
ということは…
M=15kN・m
L=5m
より、
15 = 5 × P
P = 3kN
となります。
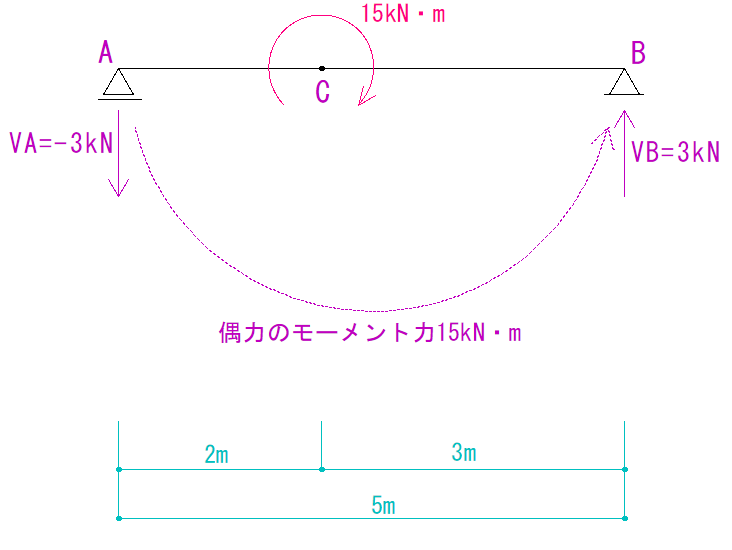
これを反時計回りの偶力になるようにセットすると…
VA=-3kN
VB=3kN
となります。
補足:モーメント荷重の反力の注意点
モーメント荷重はあまり問題に出てこないかもしれません。
なので忘れないように、しっかりと注意点を覚えておいてください。
モーメント荷重の注意点、それは…
モーメント荷重がかかる位置は反力に関係ない
モーメント荷重は、物体そのものを回す力です。
なので、どこにかかっていたとしても、物全体が回ろうとする力を持つのです。
下の図を参照
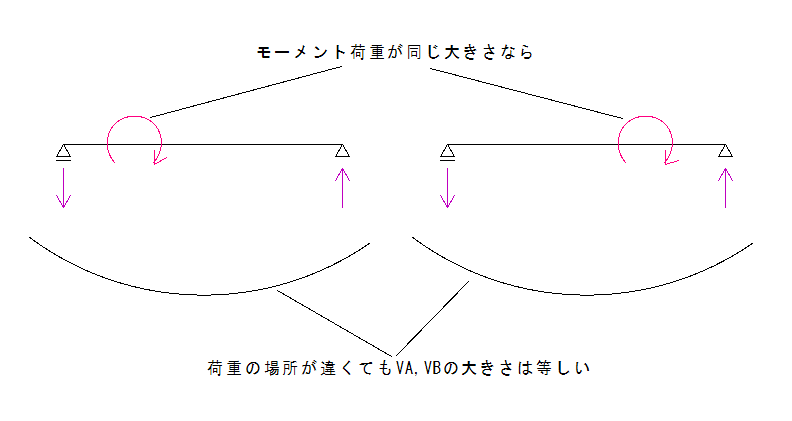
そして、このモーメント荷重の反力としてよく出てくるのが「偶力」です。
しっかりと覚えておきましょう。
Q図の描き方
では、Qを描いていきましょう。
実は今回はめちゃめちゃ簡単です。
セオリー通り鉛直方向にかかっている力のみを見てみましょう。

図の左(右でも可)を見てみます。
詳しいやり方は下の記事を参照
まずはA点を見てみましょう。
部材の左側が下向きの力でせん断されています。
この場合符号は+と-どちらでしょうか?
下の表で確認しましょう。
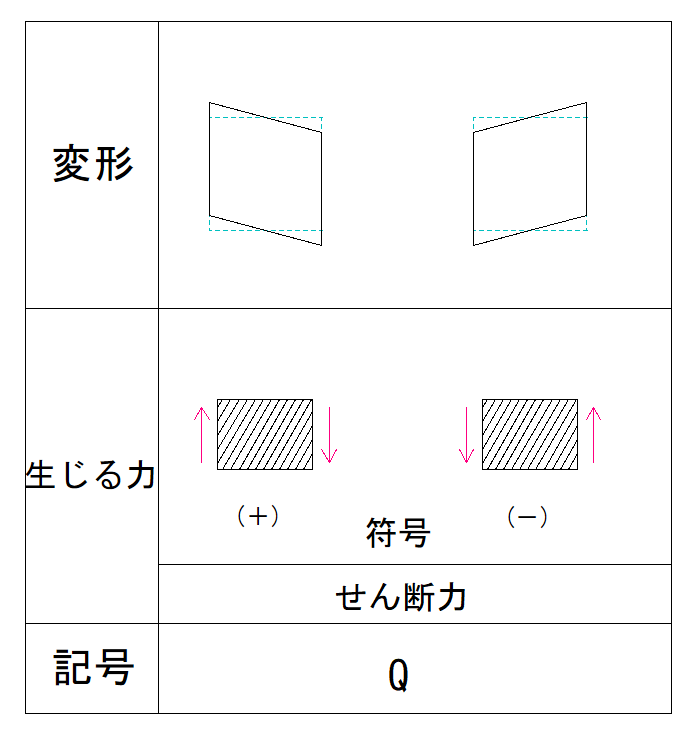
部材の左側が下向きの場合、符号は-となります。
大きさはVAのまま3kNとなります。

次に、鉛直方向にかかっている力の場所に目を動かします。
B点です。
これは部材の右側が上向きの力でせん断されています。
この場合符号は+と-どちらでしょうか?
下の表で確認しましょう。
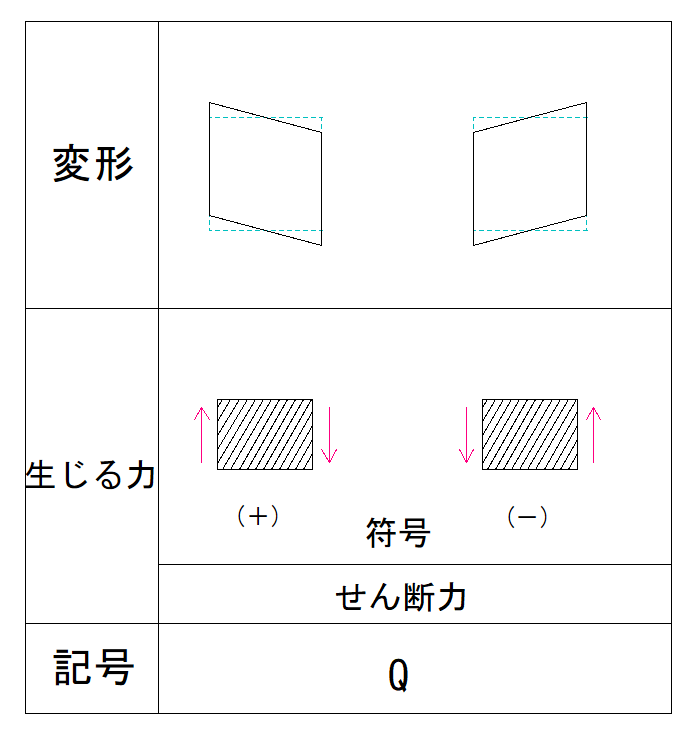
部材の右側が上向きの場合、符号は-となります。
大きさはそのまま-3kNです。

あとは直線でつなぐだけです。
最後に符号と大きさを書き入れて終了です。
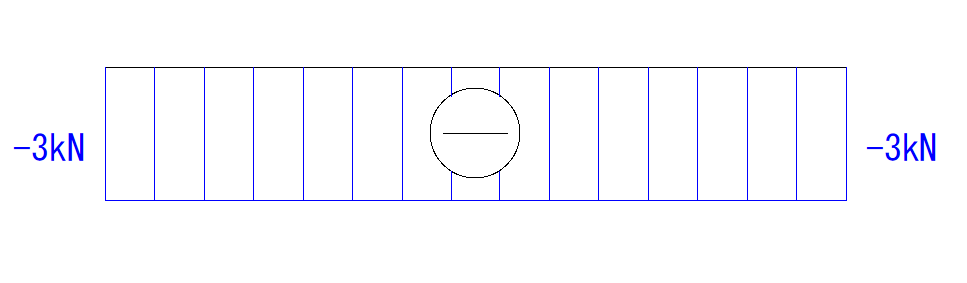
めちゃめちゃ簡単ですね。
M図の描き方
補足: モーメント荷重のM図を描くときの注意点
今回は先に補足を入れさせていただきます。
モーメント荷重ですが、モーメント力に関してある特徴があります。
それは、
モーメント力を一気に変化させる
というものです。
これを踏まえてM図を描いていきましょう。
M図の描き方 手順
今回のM図は等分布荷重や等変分布荷重ではないので、直線形になります。
では、部材の左(右でも可)から順番に見ていきましょう。
まず、A点はVAがかかっていますが、VAとA点の距離が0なのでモーメント力も0です。

次に力がかかっているのはC点です。

まず、VAがC点を回す力を考えましょう。
力のモーメントの公式より、
3kN × 2m = 6kN・m
VAはC点を上側に突き出すように回すので符号はマイナスになり、
-6kN・m
となります。
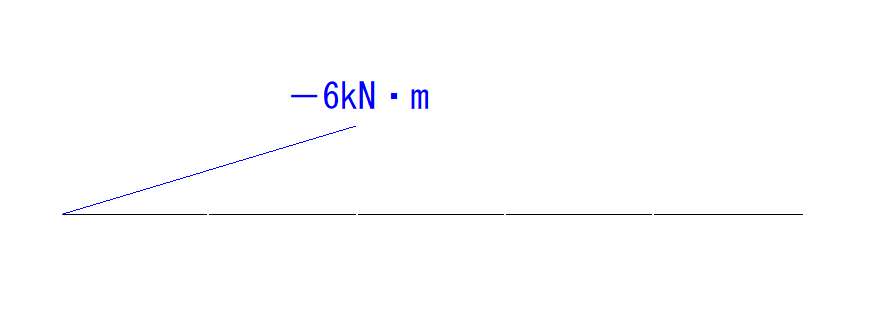
そして、先程の補足で解説しましたが、モーメント荷重はモーメント力を一気に変化させます。
今回は時計回りに15kN・mの分が一気に変化することになります。
これを式で表すと
-6kN・m + 15kN・m = 9kN・m
となり、M図も一気に変わります。
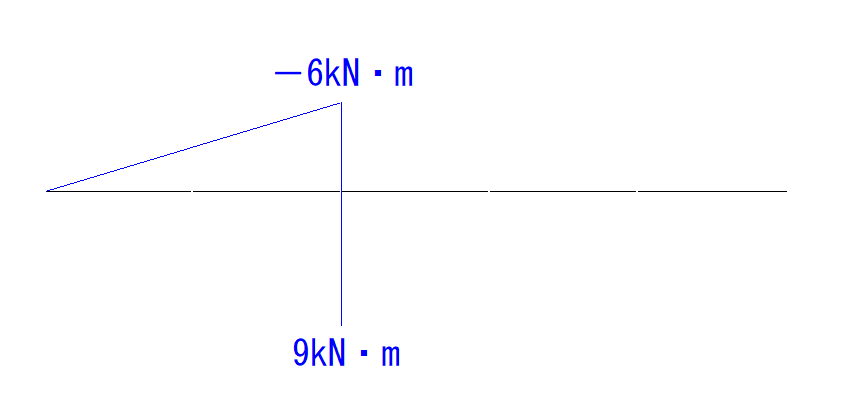
あとはB点のモーメント力と直線で結ぶだけです。
B点のモーメント力もA点と同様の理由で0なので、0に繋ぎます。
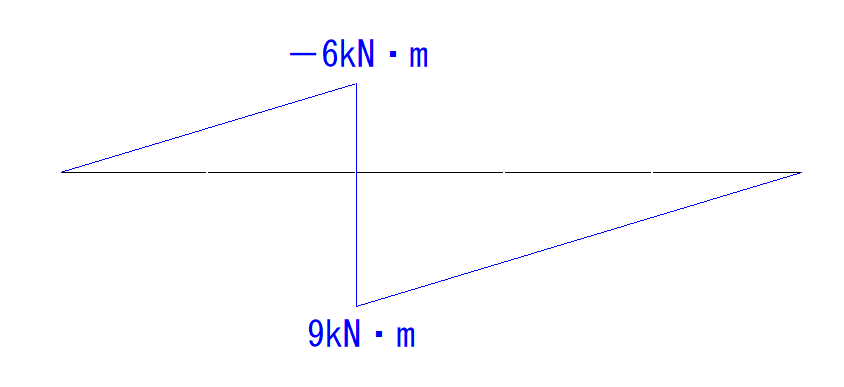
最後に符号と大きさを書き込んで終了です。