今回は先回やったN図,Q図,M図の練習を兼ねて、復習を行いたいと思います。
大事な分野なので、しっかりと理解しておきましょう。
例題
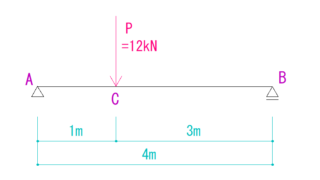
下の図を見てQ図,M図を求めなさい。

解説
反力の仮定
まずは反力の向きを仮定します。
この問題では、水平方向の力がかかっていないので、水平反力及びN図は省略します。
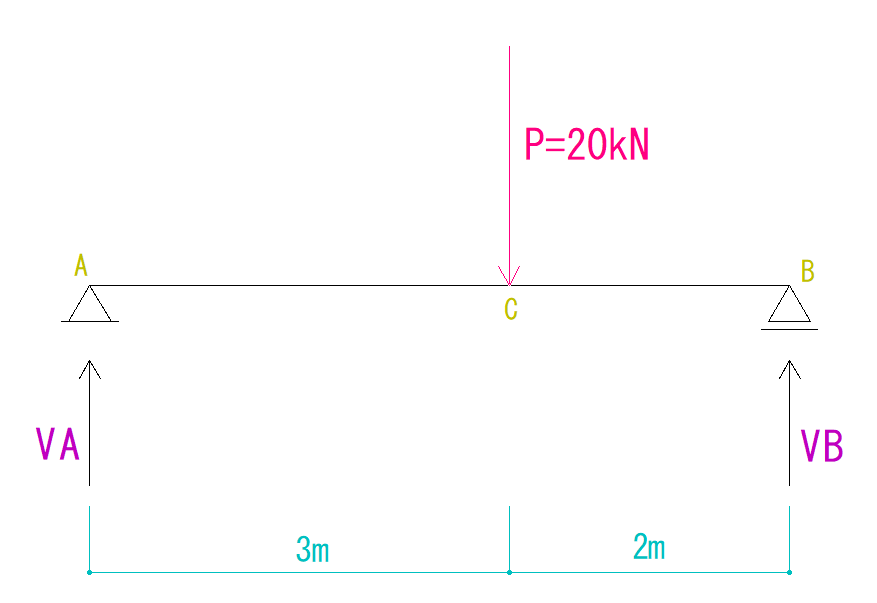
それでは反力を求めていきます。
この場合力の釣合い条件を使い、求めることができます。
単純梁に集中荷重がかかった場合の反力の求め方について詳しくは別の記事で解説しているので、今回はさらっといきたいと思います。
A点をO点として、ΣMA計算すると…
(-VB×5m)+20kN×3m=0 …※
5VB=60
VB=12kN(仮定通り上向き)
※(なぜVBにマイナスが付くかですが、仮定の向きだと、A点を反時計回りに回すためです)
ΣY=0より、
VA+12kN+(-20kN)=0
VA+12kN=20kN
VA=8kN(仮定通り上向き)
となります。

応力図の描き方
Q図の書き方
それではQ図から書いていきましょう。
やり方は覚えておられるでしょうか?
問題を右(もしくは左)から順番に見ていきます。
詳しいやり方は下の記事を参照
さて、A点を注目してみましょう。

部材の左側が上向きの力でせん断されています。
この場合符号は+と-どちらでしょうか?
下の表で確認しましょう。
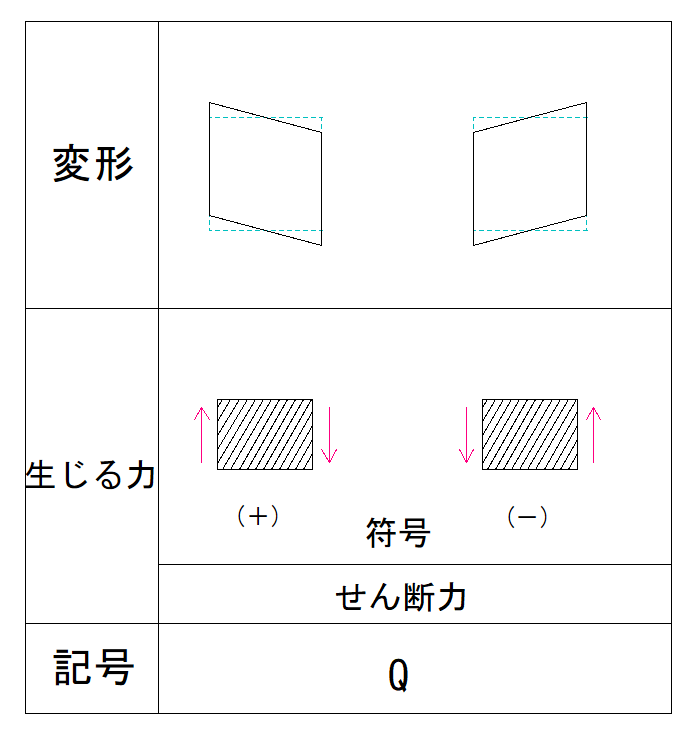
部材の左側が上向きの場合、符号は+となります。
大きさはVAのまま8kNとなります。

次に目を左側に移していくと、C点が目に入ります。
C点では下向きの力が働いています。

大きさを足してあげましょう。
【符号に注意】
+8kN+(-20kN)
=-12kN
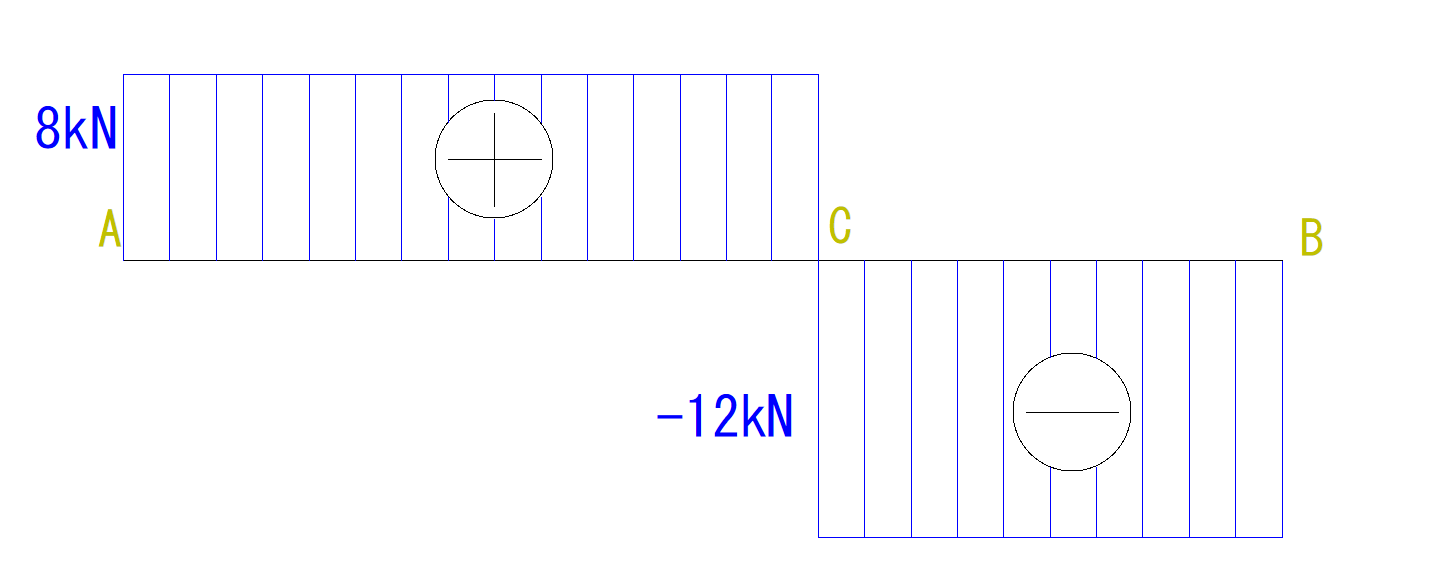
ということで、Q図は符号が変わり、-12kNのところまで落ちます。
(逆に言うとC点までは、せん断力に変化がないので、まっすぐな線になります)

最後にB点まで行くと上向きに12kN働いています。
-12kN+12kN=0
になるのを確認しつつ、Q図も0に戻ります。

最後に符号と大きさを書き入れて終了です。
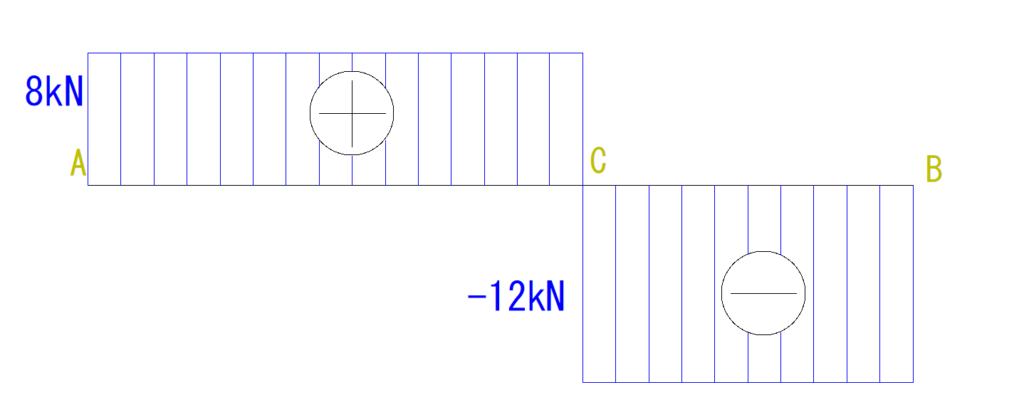
M図の書き方
M図を書いていきます。
単純梁は支点にモーメント反力がかからないので、両端が0になります。
それを踏まえて書いていきましょう。
まず、M図の書き方はモーメント反力が0のところから書き出します。
単純梁の両端はモーメント反力が0なので、今回はどちらから書き始めても良いということになります。
では、Q図と同じように左から見ていきましょう。
A点でのモーメント力は0です。
次にC点まで目をずらしていきます。
C点でのモーメント力はどれぐらいでしょうか?
VAがC点を回す力を持っているので、モーメントの公式より、
8kN×3m
=24kN・m
となります。
そして符号ですが、このVAは下の図のようなイメージで部材を曲げています。
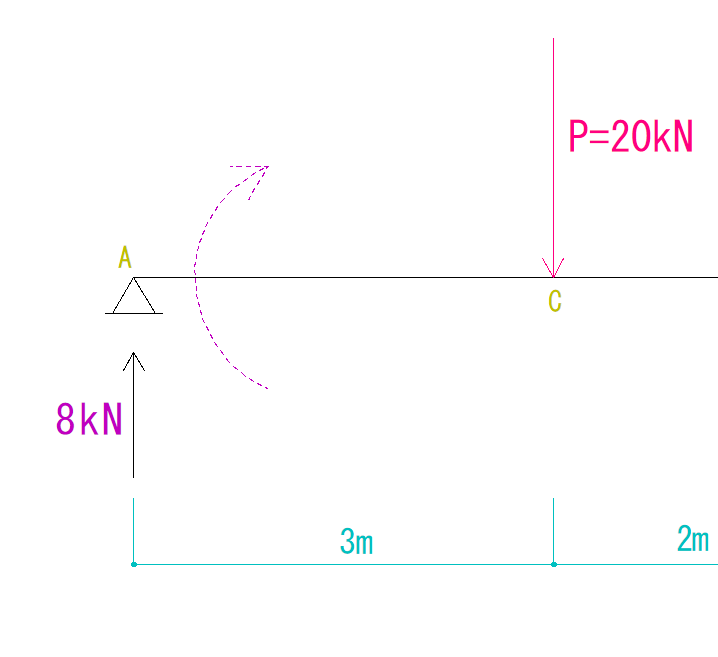
この場合+と-どちらでしょうか?
下の表で確認してみましょう。
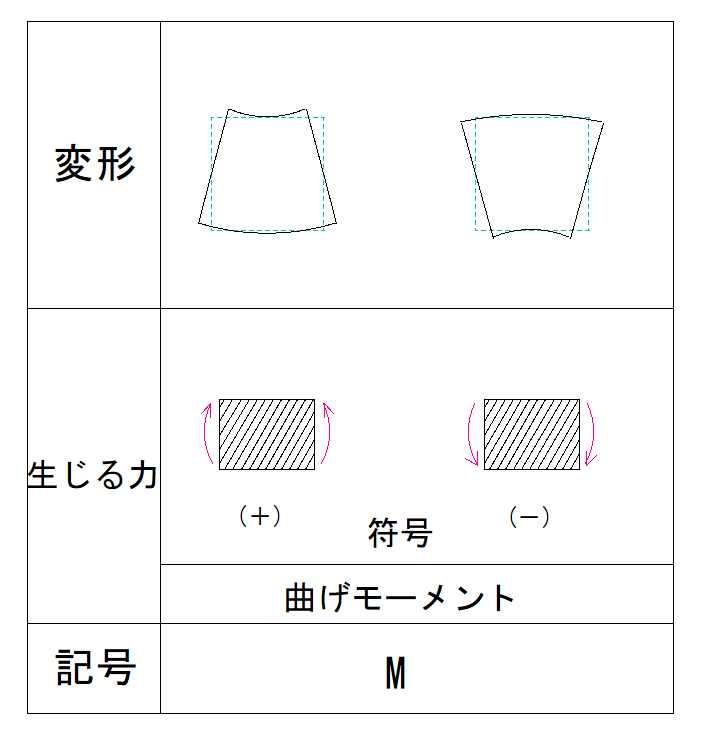
この場合は+です。
ではM図にそれを書いていきましょう。
C点のプラス方向のところに点を打ち、24kN・mとします。
そしてA点の0と線を結びます。
【注意!M図の場合、基準の線より下が+で上が-となります】

目をさらに右に移すとB点が出てきます。
B点のモーメント力は0なのでC点の24kN・mと0を線で結んだら完成です。

最後に符号と頂上の大きさを書き入れましょう。
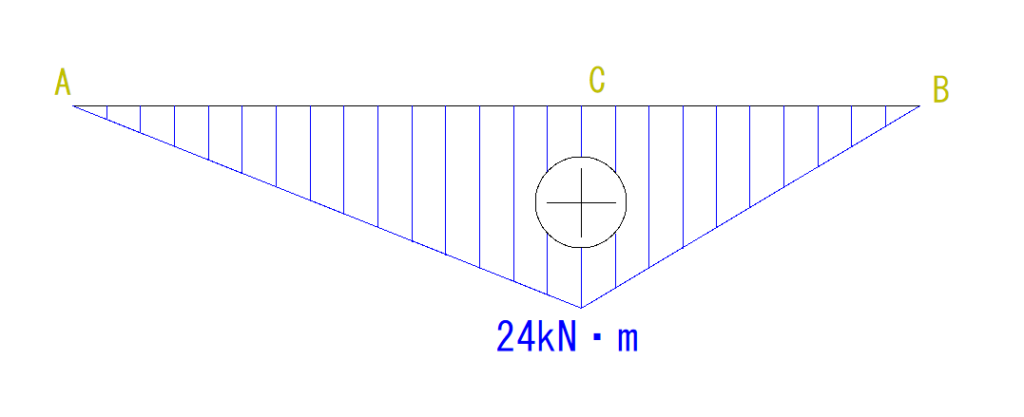
まとめ
さて、単純梁での集中荷重の問題は基本中の基本です。
そしてよく問題に出ます。
しっかりと理解しておきましょう。