この記事はTwitterから寄せられた質問に答えるものです。
興味ある方は下のリンクの記事をご覧ください。

今回は単純梁にモーメント荷重が二つかかる場合のQ図M図の描き方について解説していきたいと思います。
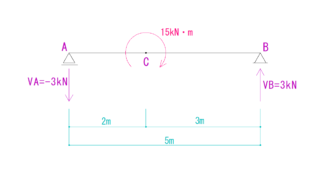
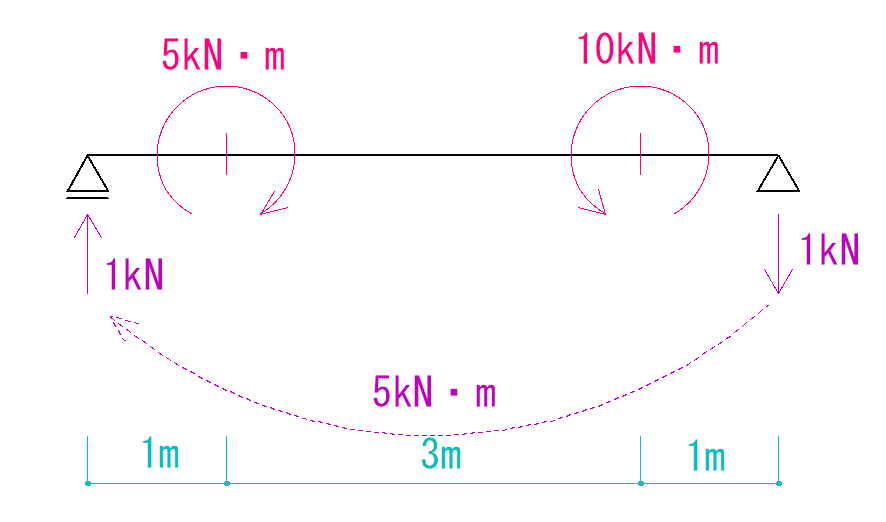
問題
下の図を見て反力を求め、Q図M図を描きなさい
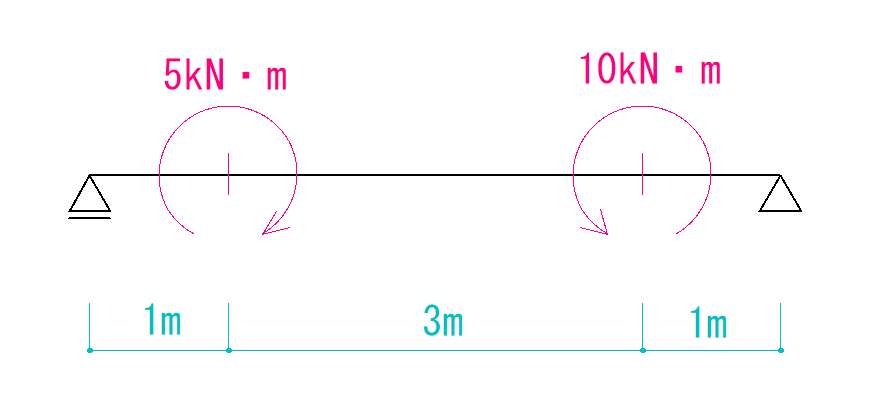
解説
今回はこの問題を使って解説していきたいと思います。
モーメント荷重が二つありますが、基本的な考え方は一つの時と同様です。
モーメント荷重が一つの時の解説記事は下のリンクを参照ください。
最初に反力を求めていきます。
反力の求め方
合力を求める
まず、モーメント荷重が二つあるので、その合力を求めます。
モーメント荷重の合力の求め方は簡単です。
ただ足すだけだからです。
今回の場合は+5kN・m(時計回り)と-10kN・m(反時計回り) ですので、
5-10=-5kN・m(反時計回り)
となります。
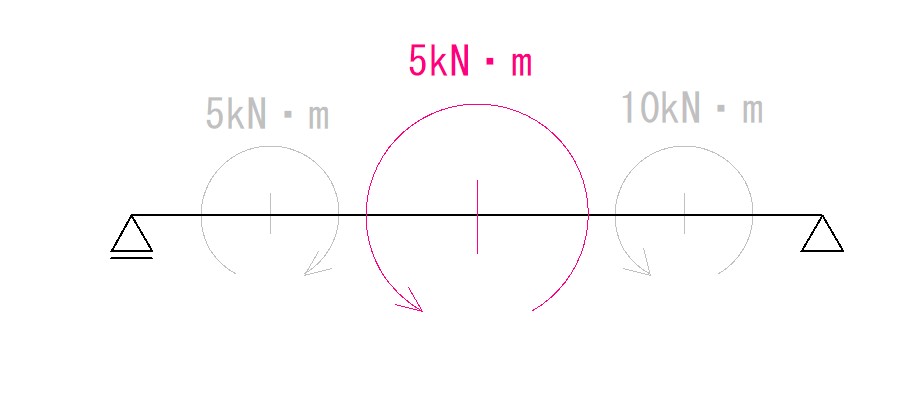
合力がかかる場所ですが、モーメント荷重は物体そのものを回す力ですので、どこにかかるわけでもありません。
ですので便宜上ど真ん中にかかることにします。
反力を求める時も、合力がかかる位置は計算上関係ありません。
反力を計算する
そしたら反力を求めましょう。
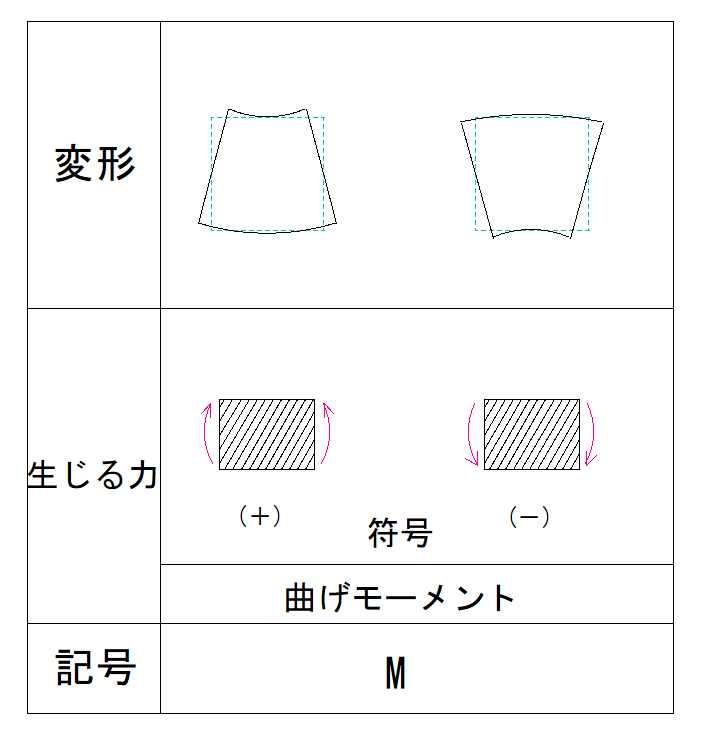
物体にかかるモーメント力に対抗できるように偶力をかけてあげればいいので下のようになります。
詳しい計算方法などは下の記事や偶力についてのまとめ記事をご覧ください。
Q図の描き方

ここまで来たらようやくQ図を描いていきましょう。
まずはせん断力だけを問題からピックアップしてみます。
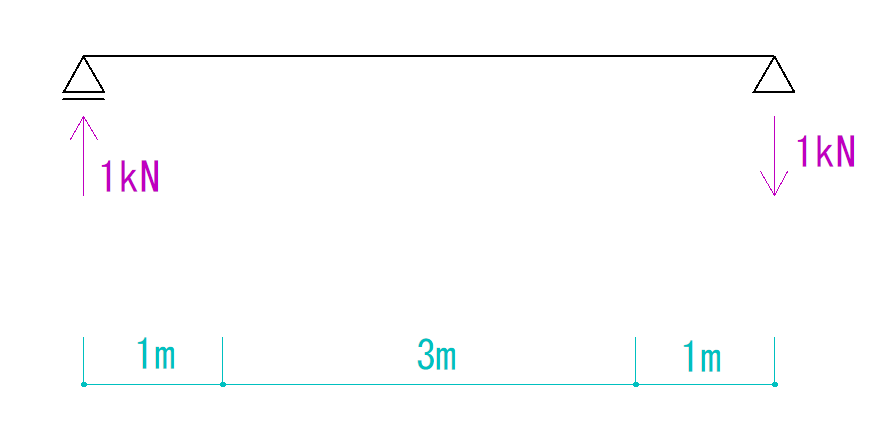
はい、反力だけですね。
モーメント荷重はせん断力に全く関係してきませんのでQ図はややこしくなりません。
ですので素直にQ図を描いていきましょう。
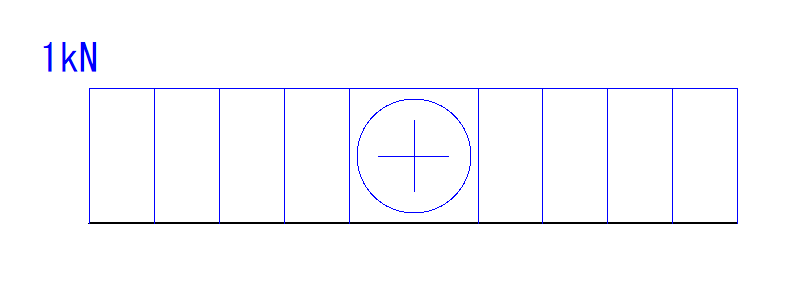
これで完成です。
モーメント荷重のみかかる場合はQ図はきれいな長方形になります。
詳しいQ図の描き方は下の記事を参照ください。
M図の描き方
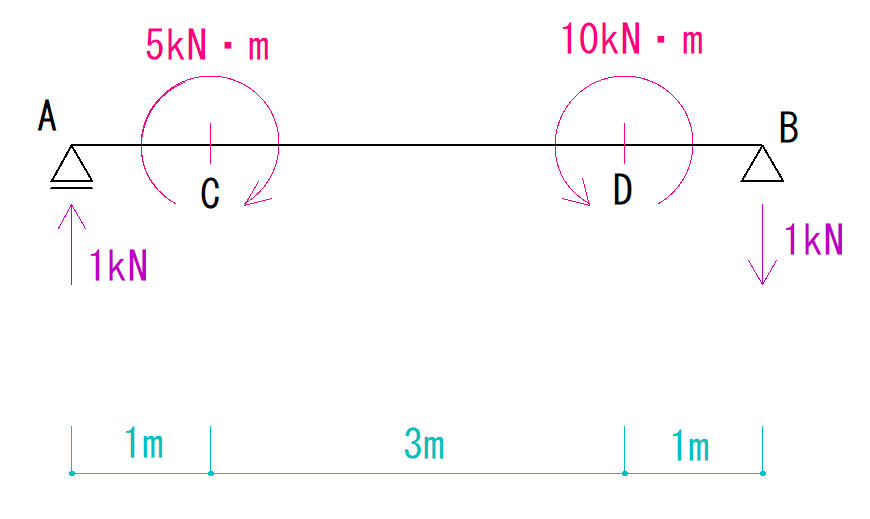
これが少し曲者です。
が、ひとつづつこれまでやってきたことを思い出しながらやっていけば解いていくことができます。
ゆっくりやっていきましょう。
A点からC点まで①
まず、セオリー通り左から(右からでも可)順番に見ていきます。
最初A点からC点までです。
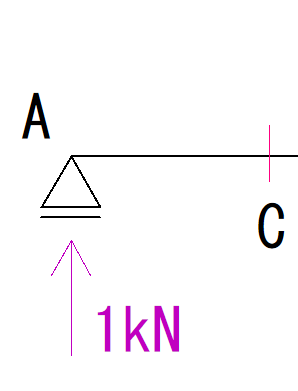
ここで注意なのは、最初からモーメント荷重ありで考えないことです。
最初は反力がC点を回す力を考えましょう。
モーメントの公式 荷重×距離 に当てはめていきます。
荷重が1kN,距離は1mなので
1×1=1kN・m(時計回り)
となります。
C点を時計回りに回す、つまり部材の下側を引っ張ているので応力図の符号はプラスになります。
参照
M図は下のようになります。

A点からC点まで②
次にモーメント荷重も含めたA点からC点を見ます。
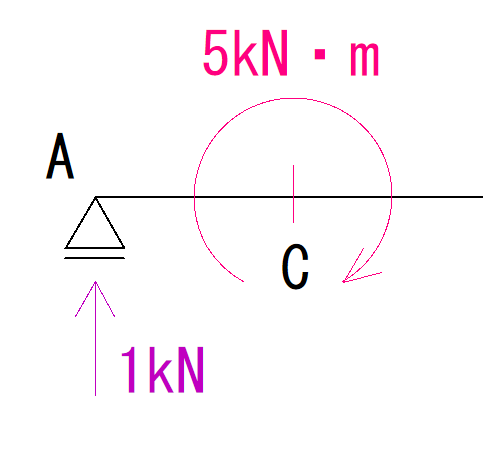
ただ、このまま考えると少しわかりづらいかもしれません。
「モーメント荷重はC点の上側を引っ張ってる?それとも下側を引っ張ってる?」となるからです。
そういう時は自分がどっち側から見てきているかを意識しましょう。
今回は左から順番に見ているので、荷重も左半分だけを見ます。
ではC点を回す力を計算しましょう。
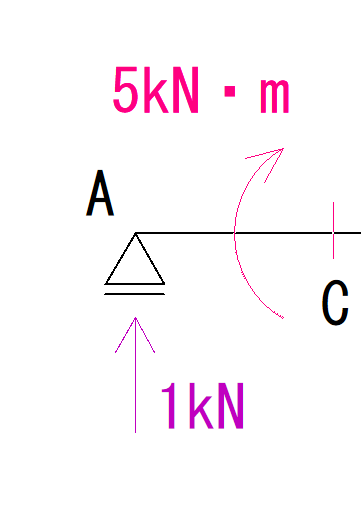
VAがC点を回す大きさと、モーメント荷重の大きさを足してあげます。
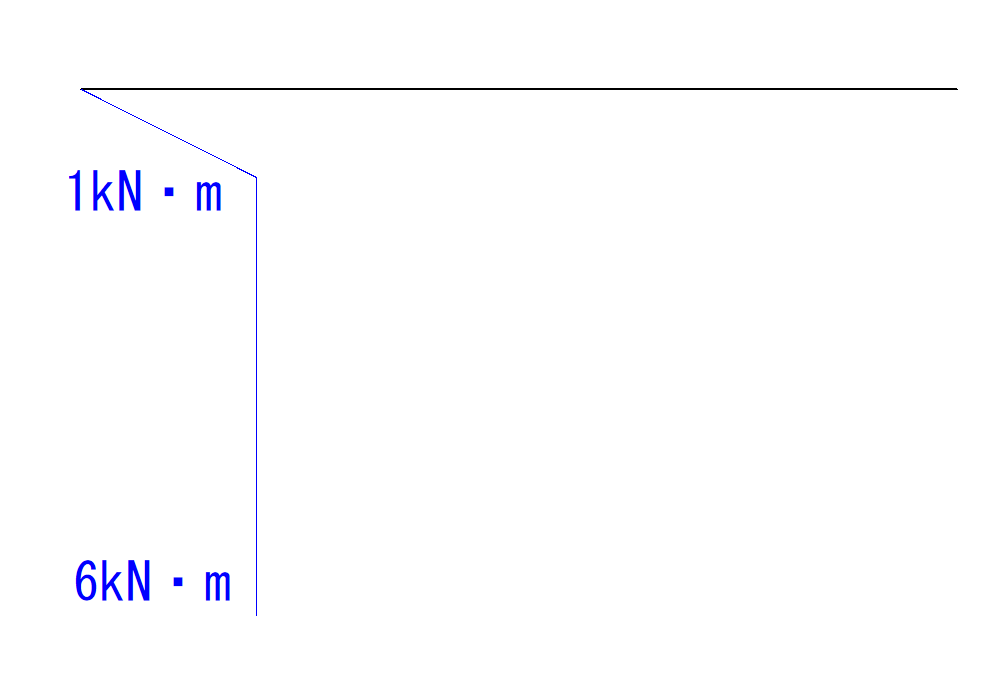
1kN・m(時計回り) + 5kN・m(時計回り) = 6kN・m(時計回り)
C点の下側を引っ張ているので応力図の符号はプラスになります。 (参照の図)
モーメント荷重はM図を一気に変化させます。
先程の1kN・mから6kN・mまで一気に変化させましょう。
B点からD点まで①
今度は右から見ていきます。
そのまま左から見ていっても解けるのですが、右から見ていけば同じことの繰り返しで解くことができるのでケアレスミスが減ると思います。
先程と同じように、まずは反力がD点を回す力を求めます。
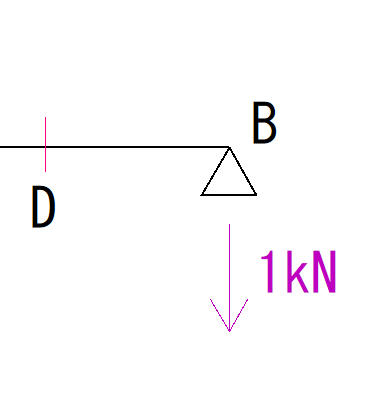
モーメントの公式 荷重×距離 に当てはめていきます。
荷重が1kN,距離は1mなので
1×1=1kN・m(時計回り)
となります。
C点を時計回りに回す、つまり部材の上側を引っ張ているので応力図の符号はマイナスになります。
(モーメントの符号と応力の符号は全くの別物なので、計算で時計回りになっても応力図ではマイナスになることもあります。
応力の符号は、部材の上を引っ張ているか、それとも下を引っ張っているかで判断しましょう。)
参照

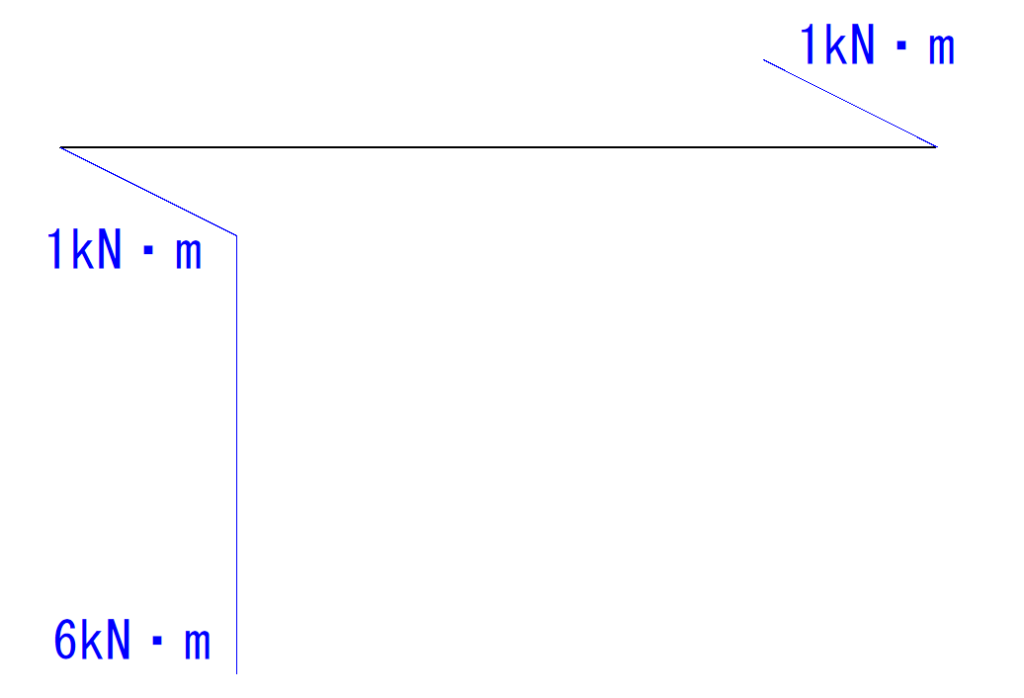
M図は下のようになります。
B点からD点まで②
次にモーメント荷重も含めたB点からD点を見ます。
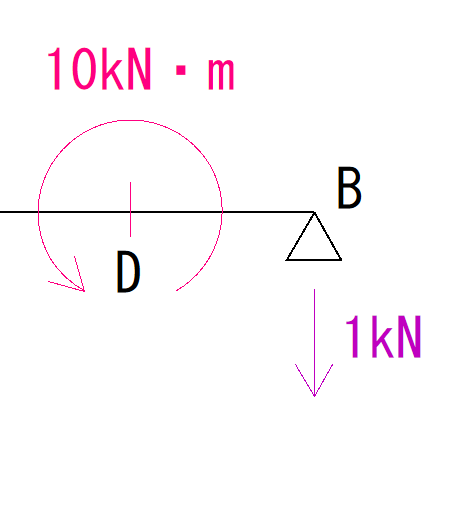
ただ、先程と同様このまま考えると少しわかりづらいかもしれません。
自分がどっち側から見てきているかを意識します
今回は右から順番に見ているので、荷重も右半分だけを見ます。
(先程とは逆です)
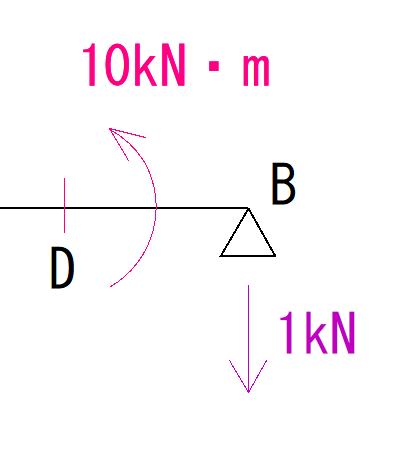
ではC点を回す力を計算しましょう。
VAがC点を回す大きさと、モーメント荷重の大きさを足してあげます。
1kN・m(時計回り) - 10kN・m(反時計回り) = -9kN・m (反時計回り)
C点の下側を引っ張ているので応力図の符号はプラスになります。 (参照の図)
今回も計算と応力の符号は逆になっています。
気を付けましょう。
モーメント荷重はM図を一気に変化させます。
先程の-1kN・mから9kN・mまで一気に変化させます。
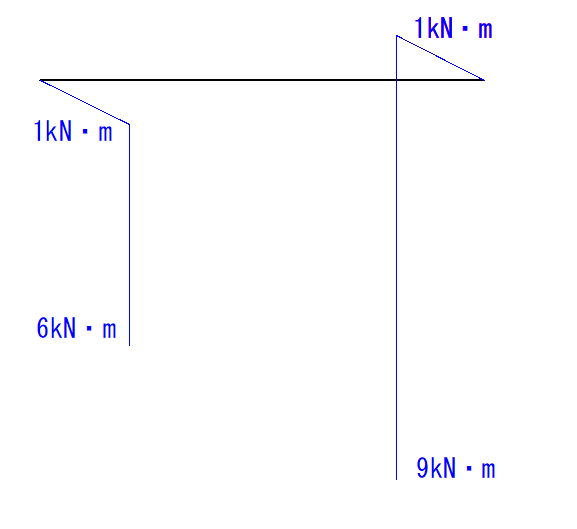
C点からD点まで
最後にC点とD点を繋ぎます。
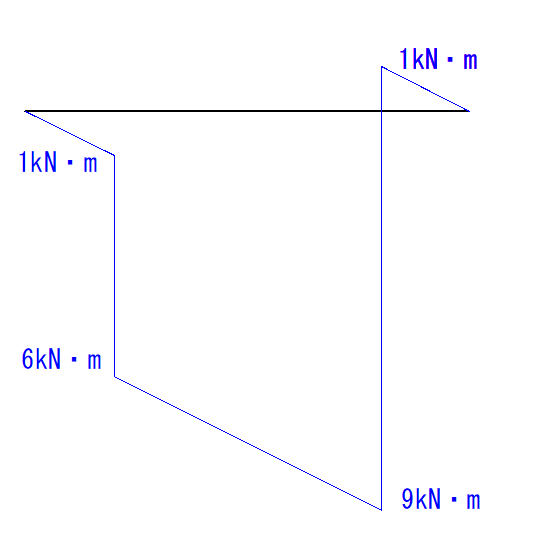
これで完成です。
例題の数値があまりよくなくていびつな形になってしまいました…
申し訳ありません。