今回は3ピン式のラーメン構造の反力の解き方の図解方法(図式解法)について解説していきたいと思います。
教科書にもあまり詳しく解説されておらず授業でもスルーされることが多い分野ですが、今回はコアなニーズに応えるべく解説していきたいと思います。
算式解法のやり方については先回の記事で解説しておりますのでそちらでご確認ください。
例題
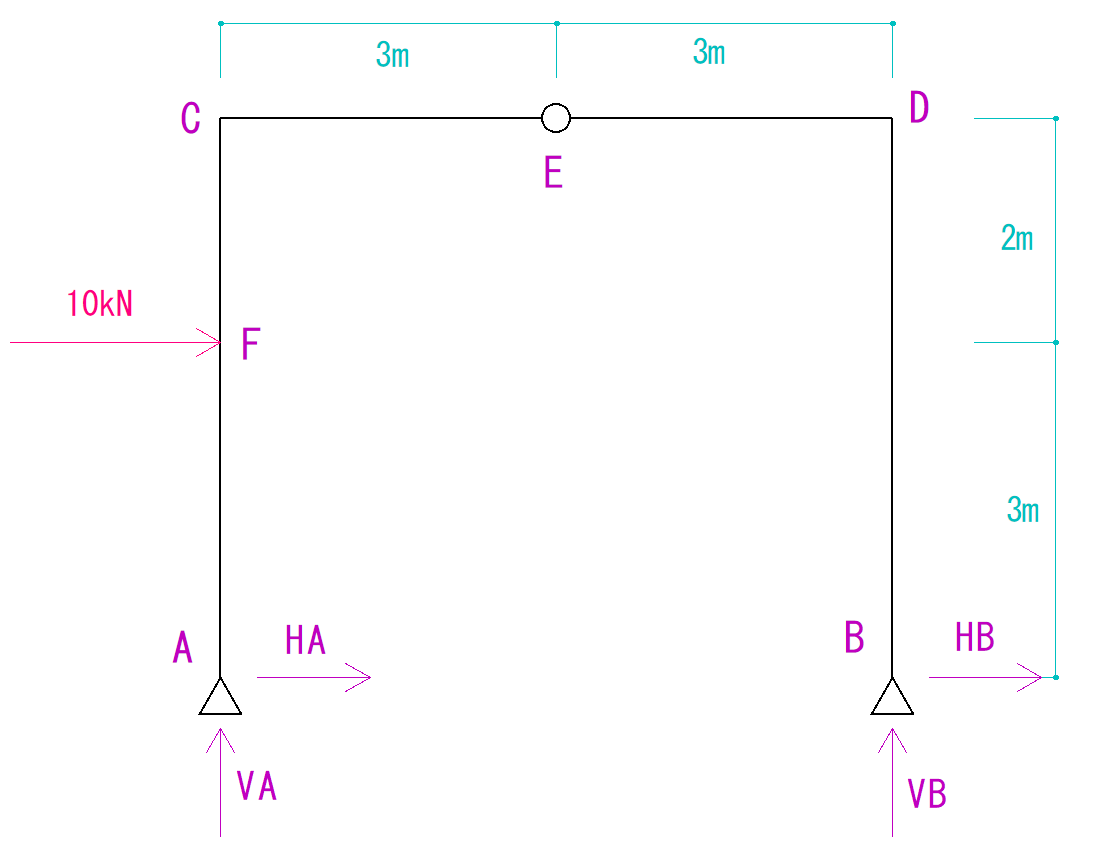
下の図を見て支点にかかるそれぞれの反力を求めなさい。
ただし1cmを1kNとします。
(サイトの都合上縮尺はずれますが、ご了承ください。)
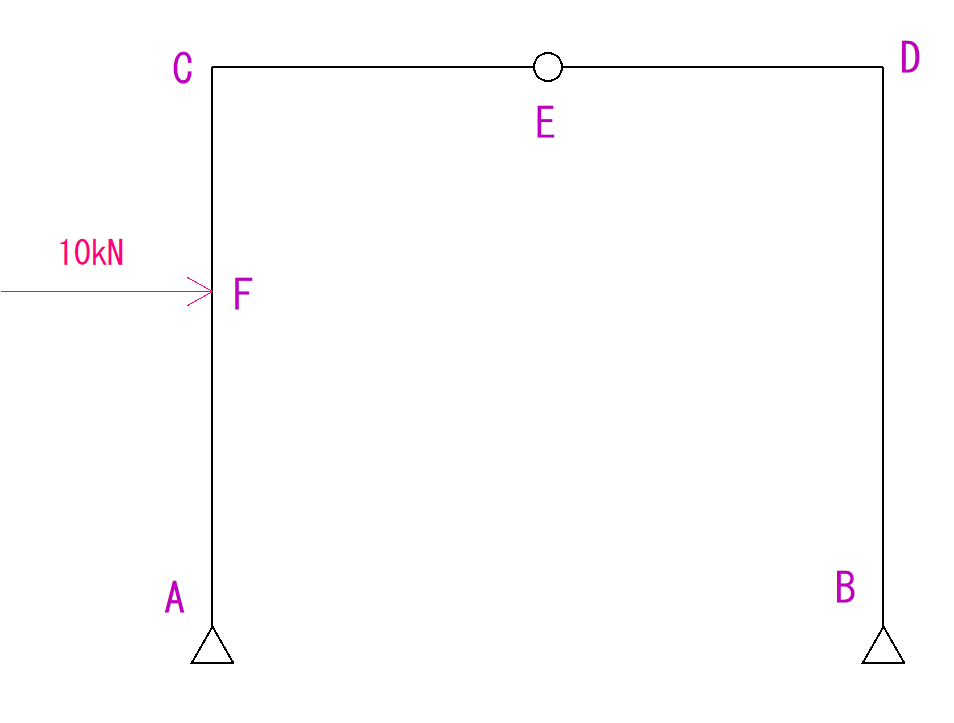
解説
まず大前提ですが、図式解法は暗記分野です。
深く考えずにただ覚えましょう。
手順①片方の支点とピン節点を結ぶ
この片方というのはどちらでもいいわけではありません。
力がかかっていない側の支点とピン節点を結ぶということです。
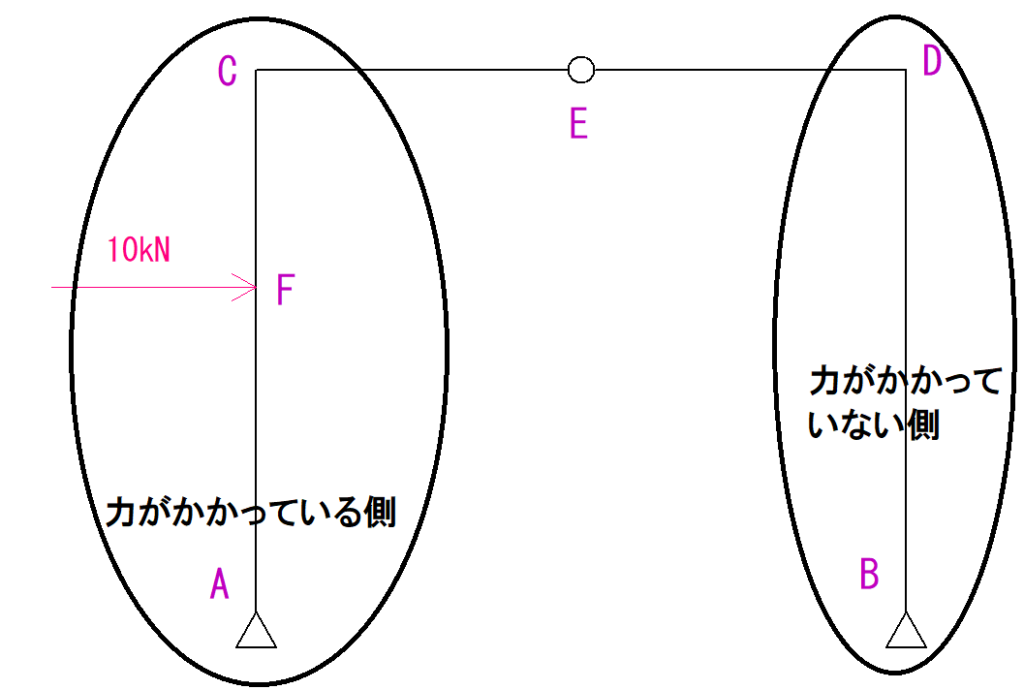
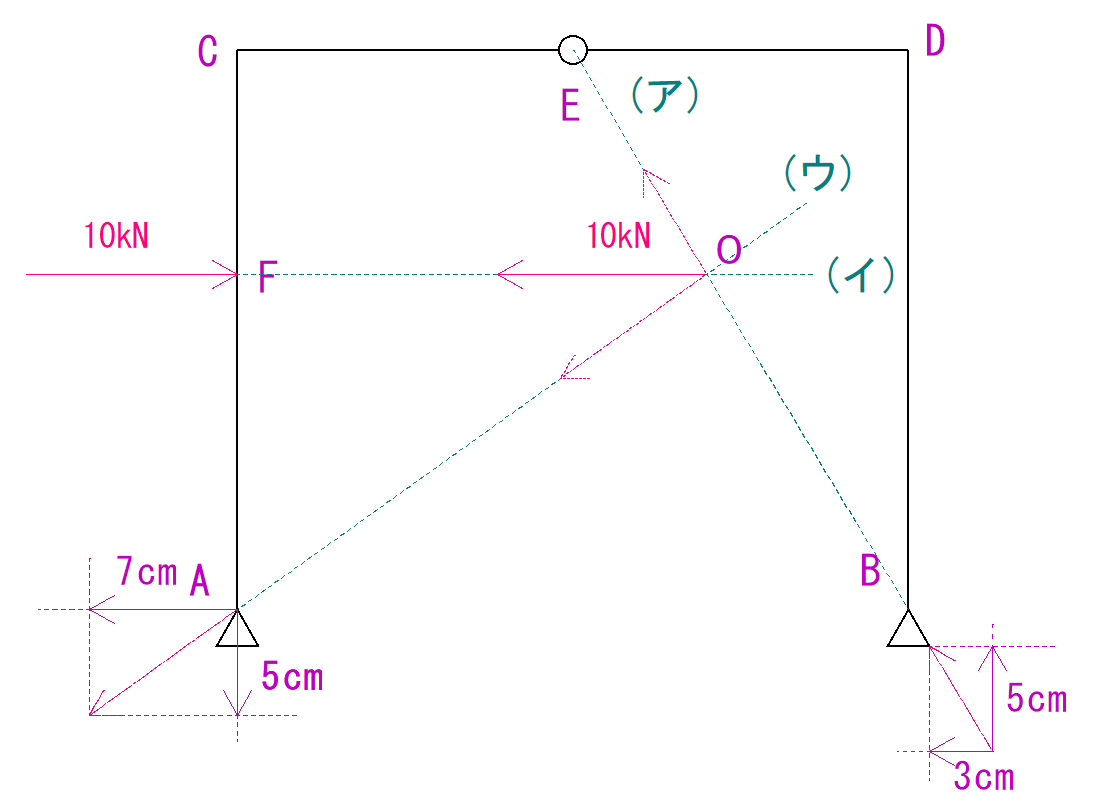
今回はB点からE点までの線を結ぶことになります。
この線を(ア)線と呼ぶことにします。
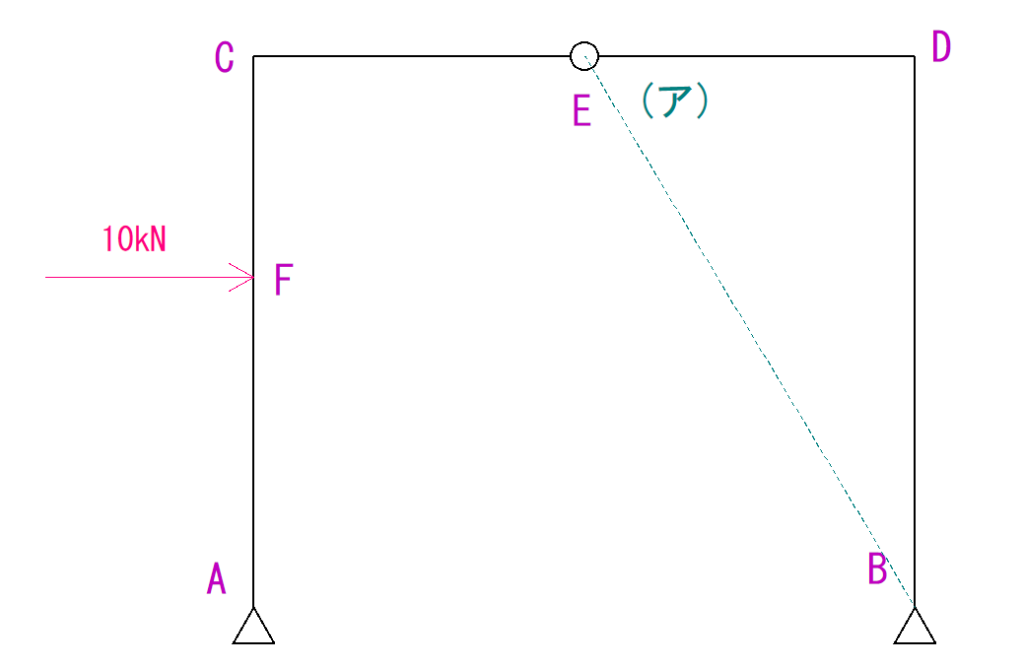
(ア)線はB点にかかる反力の作用線となります。
手順②荷重の作用線を延長する
ここは簡単です。
ただ荷重の線をまっすぐ伸ばし、(ア)線と交差させます。
これを(イ)線と呼ぶことにします。
そして交点をO点とします。
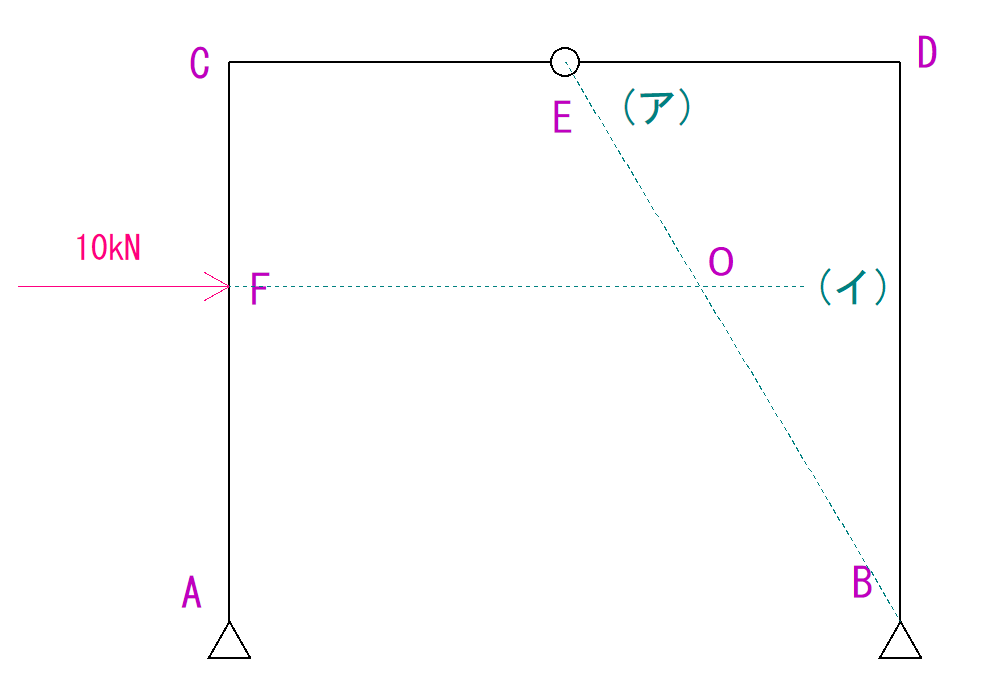
手順③もう片方の支点からO点までの線を結びます。
この線を(ウ)線と呼ぶことにします。
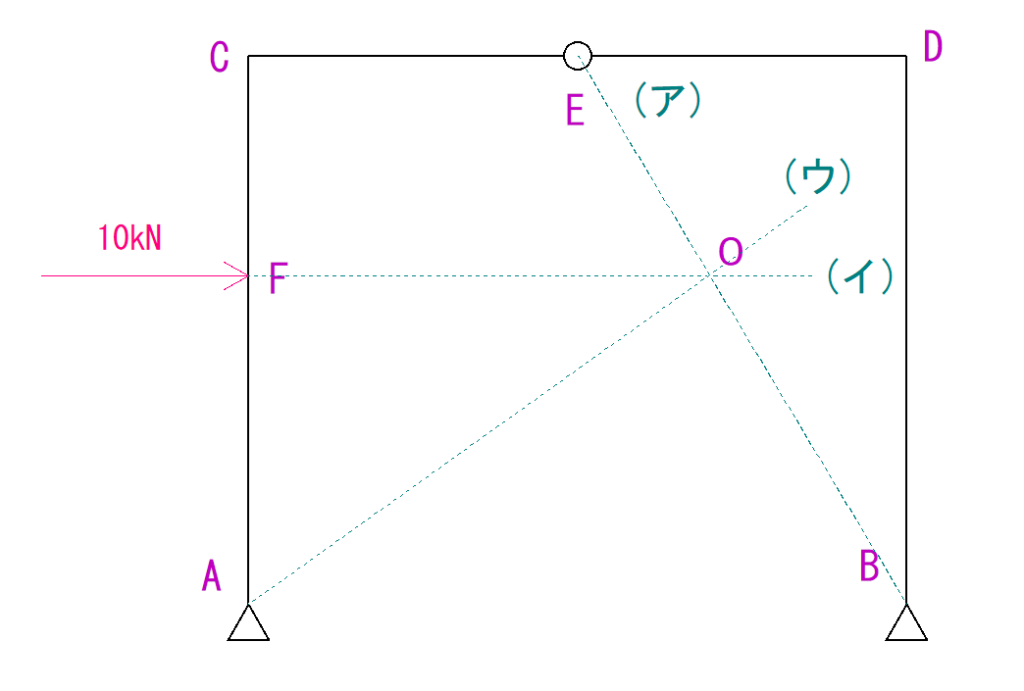
手順④荷重への反力の分解をする。
ここから少し難しくなります。
まず、O点を原点に、荷重と同じ力を反対方向に書きます。
(矢印の大きさが問題の縮尺と同じになるようにしましょう。)
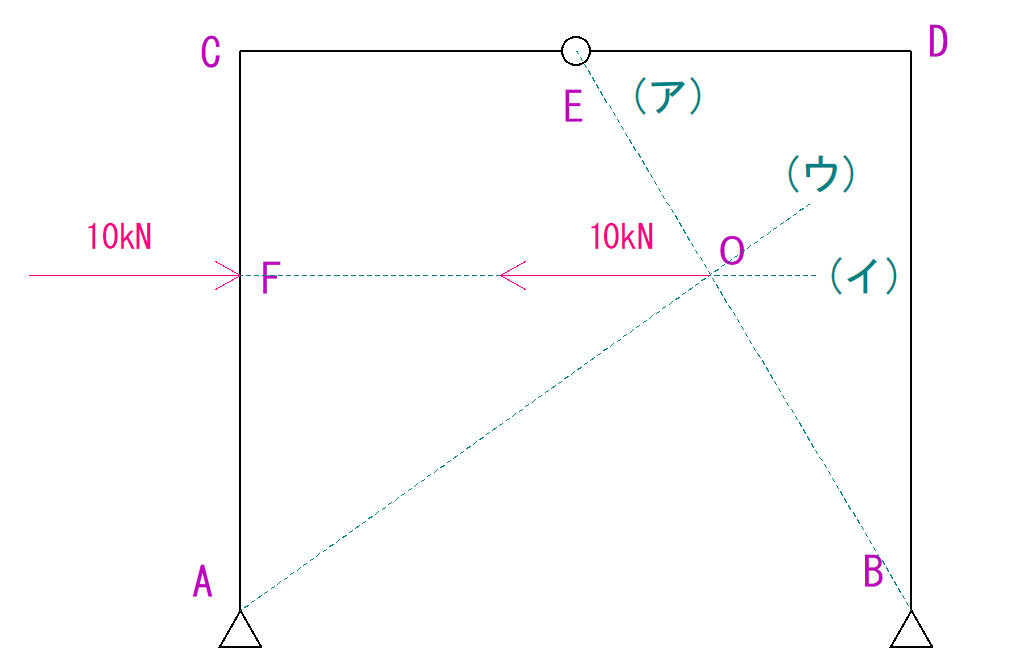
そうしたら、その反力を(ア)線と(ウ)線で分解します。
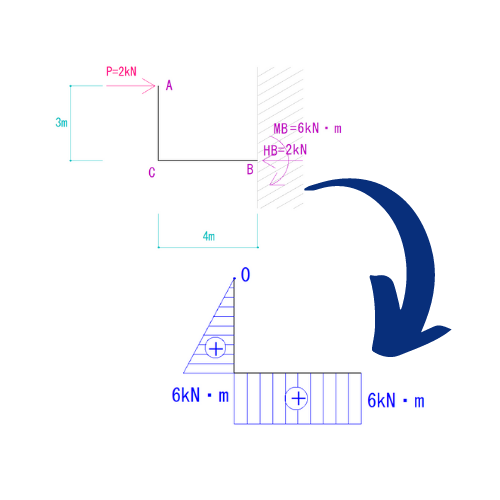
詳しいやり方は下のリンクの記事からご覧ください。
解くと下のようになるかと思います。
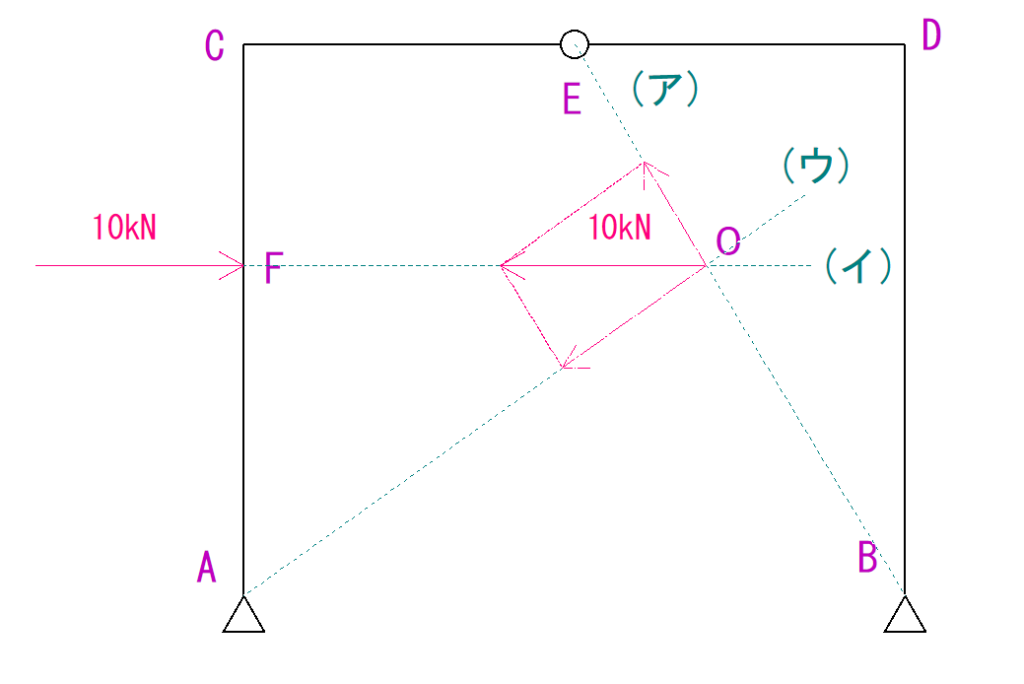
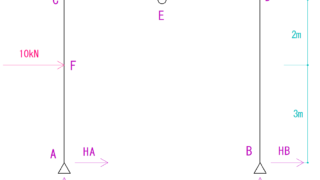
手順⑤それぞれの支点にかかる反力を分解する
先程求めた分力を、作用線上を移動させて支点に持ってきます。
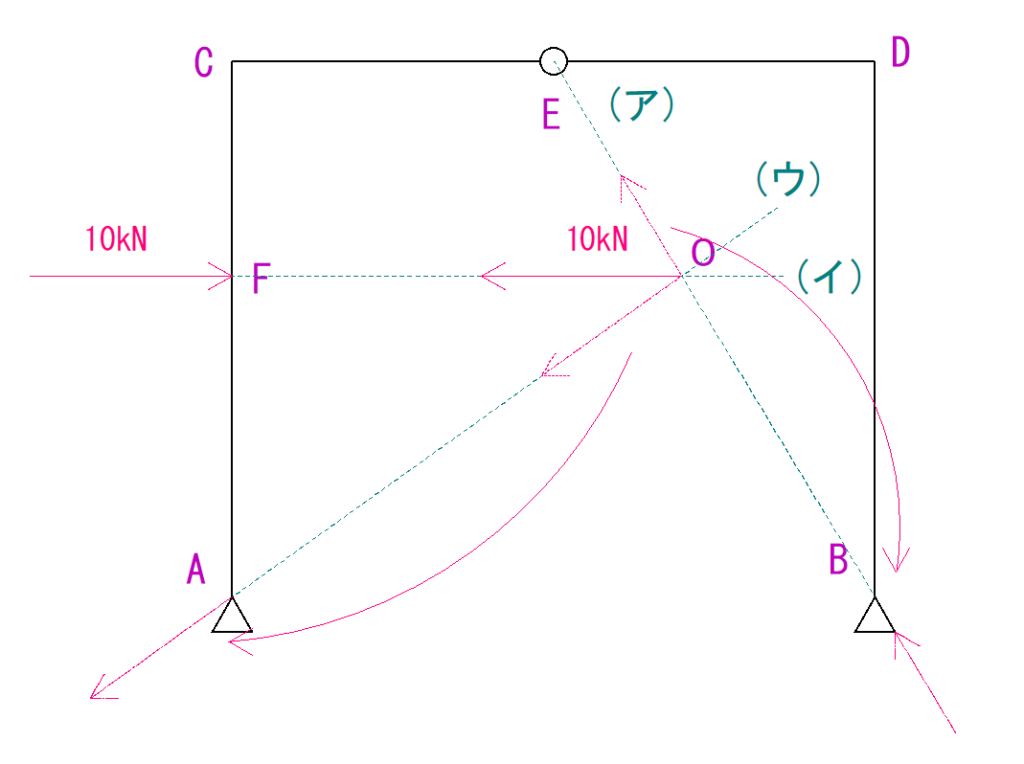
そしたらそれを、水平方向の力と鉛直(垂直)方向の力に分解します。
こちらも詳しいやり方は下のリンクの記事をご覧ください。
解くと下の図のようになります。
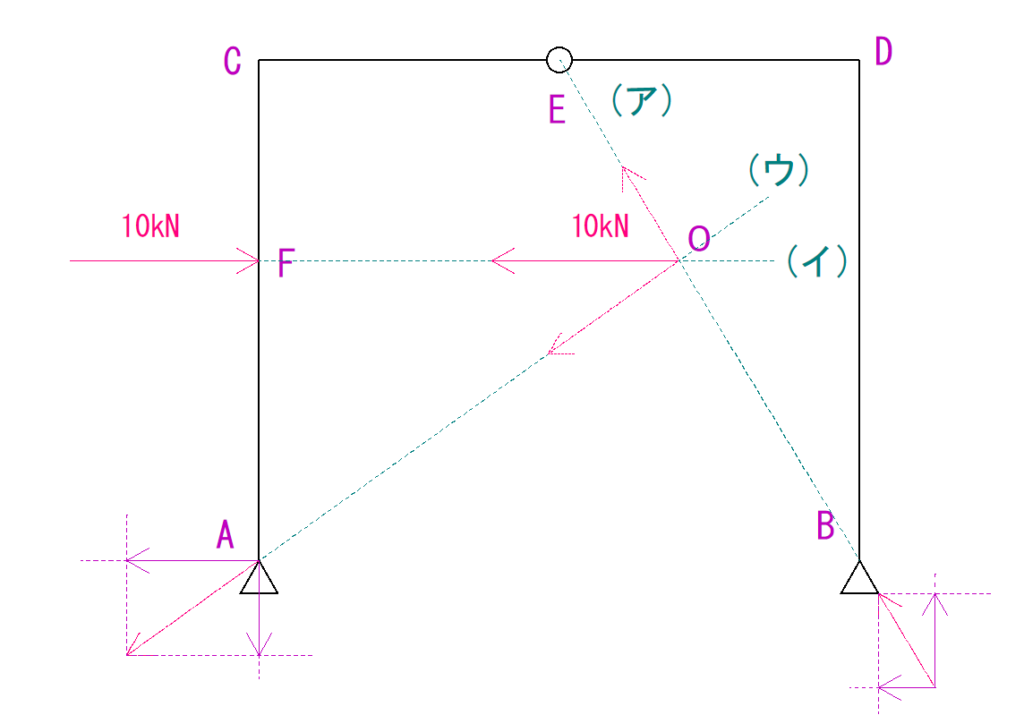
手順⑥長さを測り反力の大きさを求める。
あとは作図したそれぞれの反力の長さを測り、大きさを求めます。
うまくいくと下のようになるかと思います。
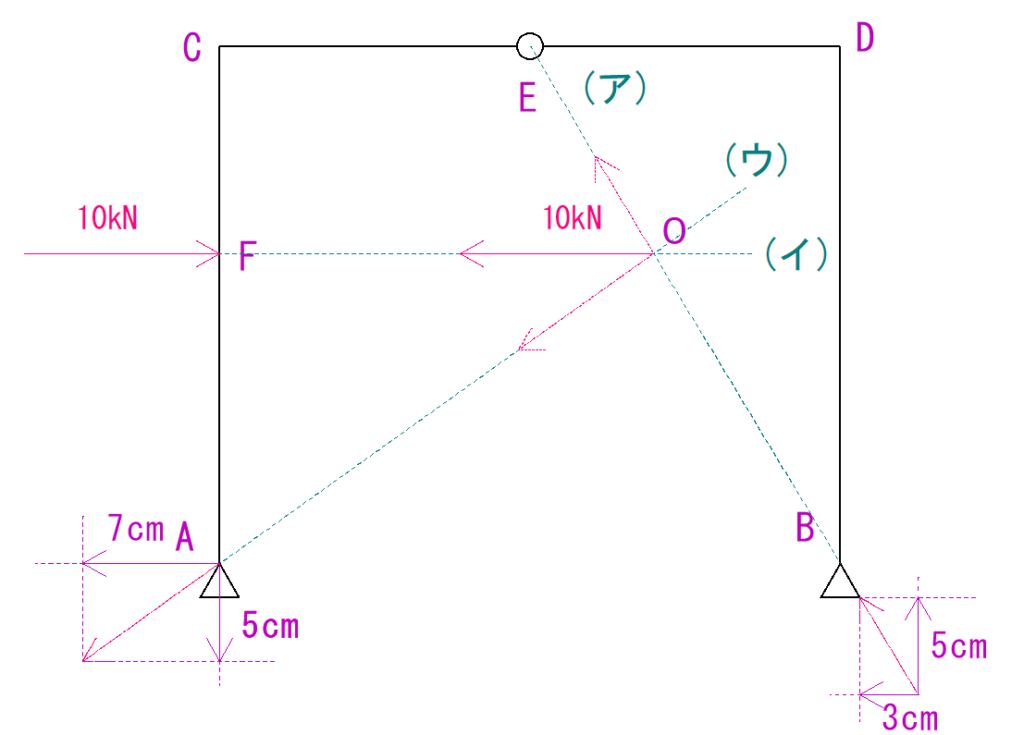
解答
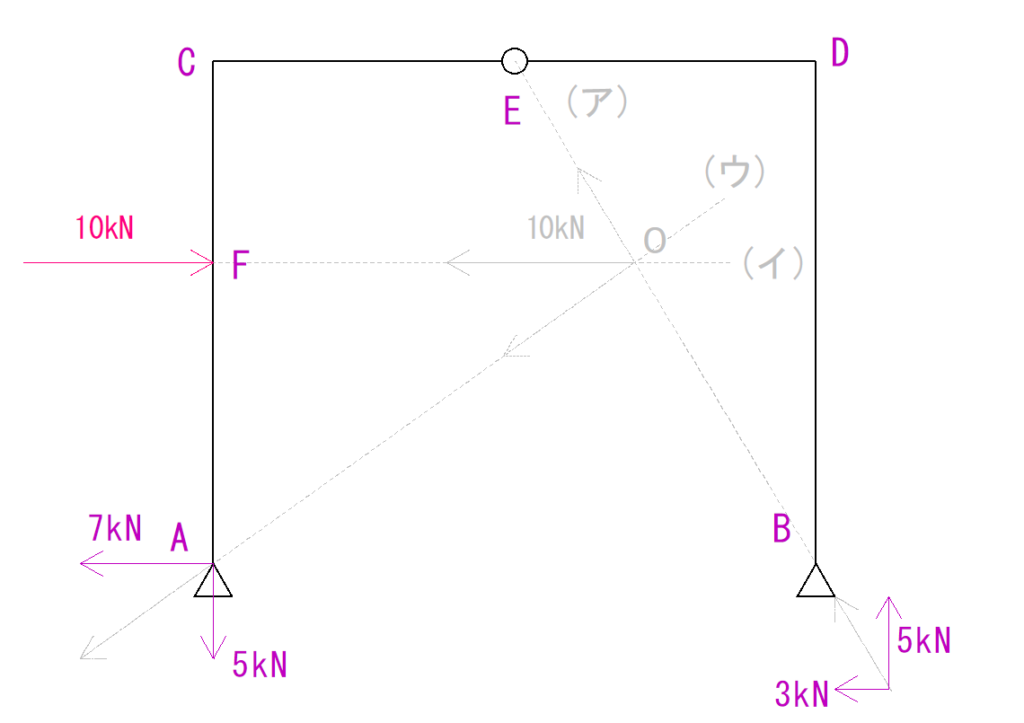
まとめ
3ピン式ラーメンについてあまり詳しくやらないところも多いので、それの作図方法はテストにも出てこない可能性は高いです。
ただ、知識として知っておいて損はないので参考までに覚えておきましょう。