今回は三角比についての記事を書きたいと思います。
この構造設計の分野において重要な三角比ですが、しっかりと理解しておかないと後々つらい目にあいますので、一度ここで確認しておきましょう。
三角比ってなに?
さて三角比ですが、「三角比って何?」と聞かれてぱっと答えられるでしょうか?
今回はこれを簡単に解説していこうと思います。
まぁ本当に簡単に言うと、
三角形の辺の比率
…というそのまんまになってしまうのですが、もう少しかみ砕いて説明します。
(前提の話ですが、ここでの三角比とは直角三角形の三角比について解説しています)
三角比を簡単に理解してみよう
三角比を語るには直角三角形を用意しないといけません。
ということで下の画像をご覧ください。
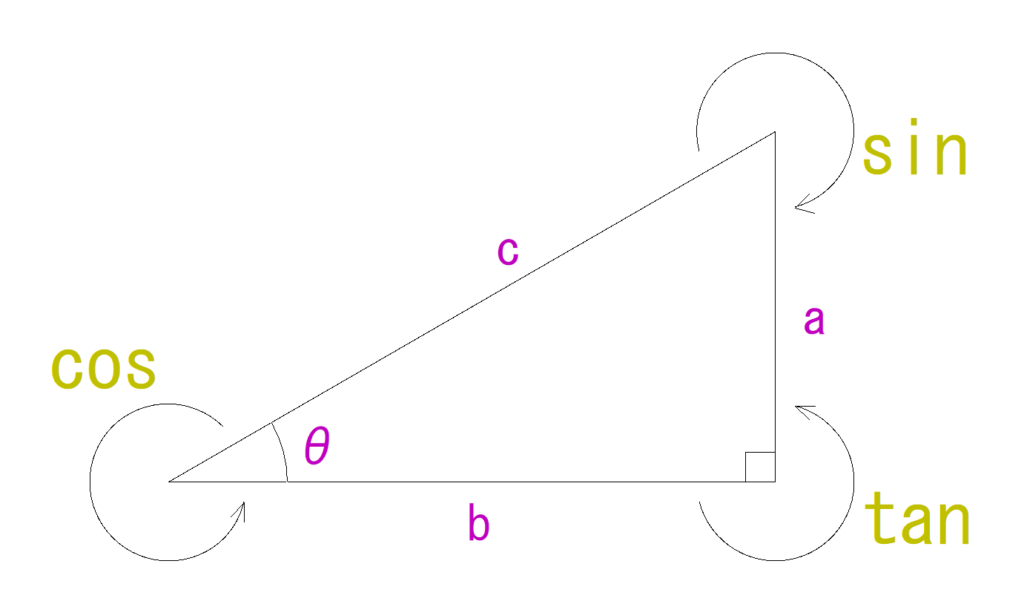
…まぁよく見る図だと思います。
要は、これで何が分かるのか?何を求められるの?ということですよね。
そこの意味を解説していきます!
実は直角三角形ってすごく使いやすい三角形なんです。
なぜ使いやすいのか。
それは、
各辺の比率が決まっているから
です。
何言ってるの? という感じでしょうか。
もう少し詳しく説明していきます。
下の三角形を見てください。

それぞれの辺が3㎝4㎝5㎝になっています。
この時の三角形の赤いところの角度は約37°になっています。
では、その角度を維持しつつ大きくしてみましょう。

そうすると9㎝12㎝15㎝になりました。
まぁそりゃそうですよね。
相似の三角形の辺を3倍にしただけです。
でも、ここが大事です。
a : b : c
3㎝:4㎝:5㎝
9㎝:12㎝:15㎝
3 : 4 : 5
これって比率は変わっていませんよね。
つまり、大きさがどんなに変わっても、直角とそのほかの角度が決まっていれば、3辺の比率は決まるのです。
これが三角比です!
これすごい便利じゃないですか?
比率が分かっちゃえば、辺の長さを求めるときに、いちいち2乗して足してルートに入れて…とかしなくていいんです!
では、よく問題に出る三角形を並べておきます。

これらの三角比を覚えておくのと覚えないのとでは、大きな差が出ます!
これから問題文で60°,30°,45°などが出てきたら要確認です!
そういう数字が出てきたら、大体この三角形の辺の比率を活かして答えることができます。
また3:4:5の三角形もよく出てきます。
6㎝10㎝とか9㎝12㎝などの組み合わせで問題文に出ることが多々あります。
ぜひチェックしておきましょう!
さて、では確認問題です。
下の三角形の辺の長さを求めなさい。

解答
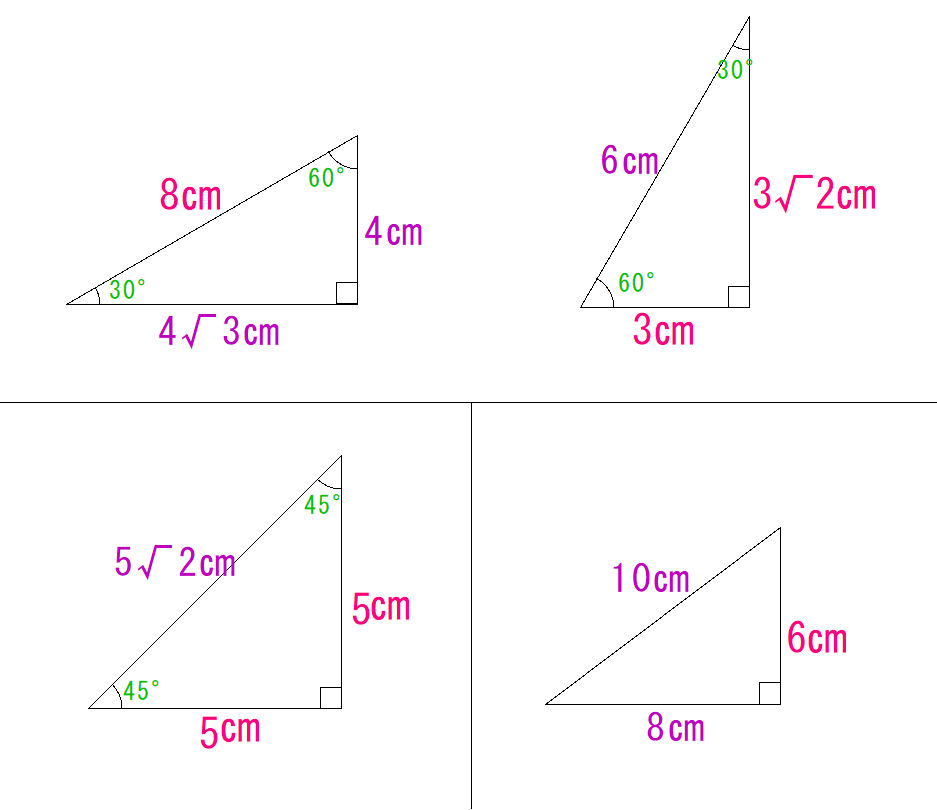
これは簡単でしたね。
ぜひ完璧にマスターしておきましょう!
sin,cos,tanとは?一番の難関です
さて、つまずく人が多くなるのはこの分野ではないでしょうか?
サインコサインタンジェント…
この言葉を聞くだけで拒否反応が出る、なんていう友達もいました。
でも安心してください!
この記事を見終えるころには、
「なんだ、そんなことか!」
となっているはずです!
では早速解説していきます。
先程の三角比の話の続きなのですが、昔の人はあることを発見しました。
「これ、直角三角形の2辺が分かれば直角以外の角度も分かるんじゃね?」
…と。
なんでそうなるのか、気になる方のために解説します。
なんでsin,cos,tanで角度が分かる?
まず、直角三角形は比率が決まっていると先程確認しました。
引き続き3:4:5の三角形の例で考えてみましょう。

この3:4:5の三角形はこの形しかありえません。
ということは、角度は一定です。
大きさが変わろうと、これ以外の角度になることはありえません。

次に確認ですが、直角三角形は2つの辺の長さが決まると、もう1つの辺の長さは必然的に決まります。
なぜか、
直角三角形の斜辺を求める公式を思い出してください。

このように、2つの辺が分かればもう1つも計算で出せるのです。
勘のいい方ならもうお気づきかもしれません。
実は、三角比はわざわざ3つもそろえる必要はないんです。
2辺の長さが分かる→もう1つの辺の長さが分かる→三角比が出る
ということは…
2辺の長さが分かる→三角比が出る
となるのです!
さて、これまで三角比は3:4:5みたいな比率のことだ!と言ってきましたが、これは実は正確ではありません。
…いや、正確ではあるのですが、一般的には別の方法で表します。
これらを見たことはあるでしょうか?

これがいわゆる三角比と呼ばれるやつです。
この分数の意味が分からないですよね…
簡単に解説していきます!
またまた先程の続きになります。
昔の人は気づきました。
「これ、辺の比率が決まったら分数にしちゃえばいいんじゃない?」
…ということで分数にします。
「…分度器でいちいち図るのめんどいから、この分数で角度を表せばええやん!」
という感じでsin,cos,tanが誕生しました。
(脚注:これまでの昔の人の話は完全な想像です。事実とは絶対一致しません。わかりやすく考えるためのイメージです。ご了承ください…)
ただこの発見のおかげで、辺の長さの比が分かれば角度を知ることができるようになりました。
また逆に、角度が分かれば三角比が分かります。
しかし、この分数は何度…と全部覚えるのは無理です。
そこは関数電卓を使って求めましょう。
(関数電卓がない方は三角比の表を見て求めることができます)
さて、ここまでの流れでなんとなく理解できたでしょうか?
三角比を深く理解しようとすればするほどわけわからなくなっていきます。
どこかで区切りをつけて、こういうものなのかぁ…程度に考えましょう。