「節点法」の算式解法について今回はやっていきます。
算式解法は、トラスを解く場合よく使います。
しっかりと理解しておきましょう。
この「節点法」算式解法は三角比を用います。
sin,cos,tan…というものです。
そちらについては別記事で解説していますので、復習したい場合は下のリンクの記事をご覧ください。
例題
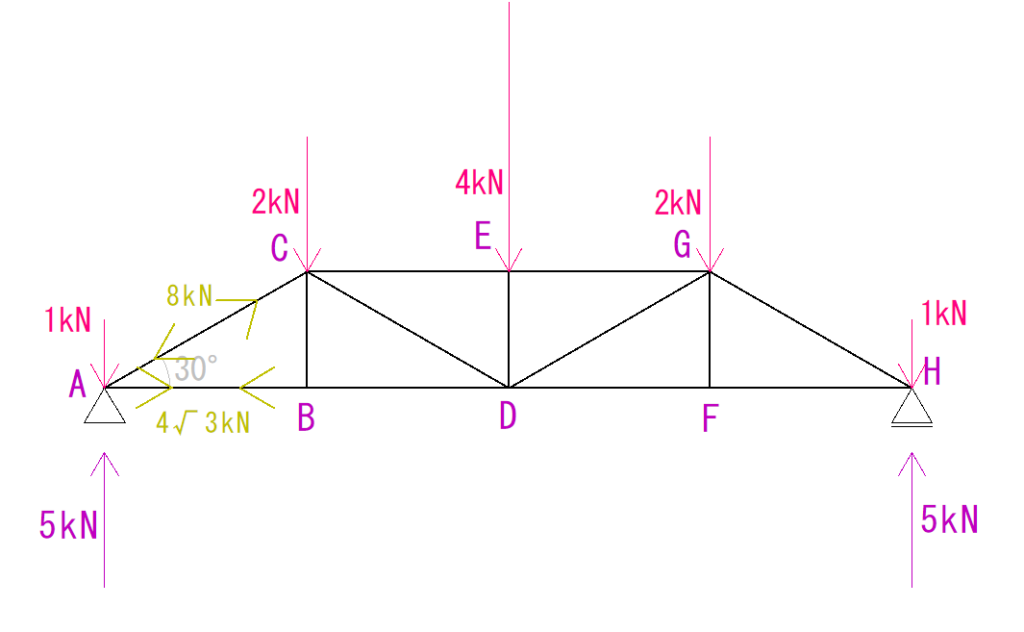
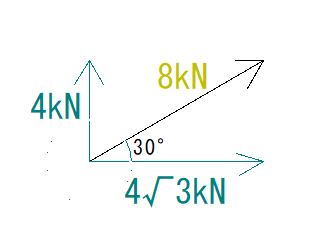
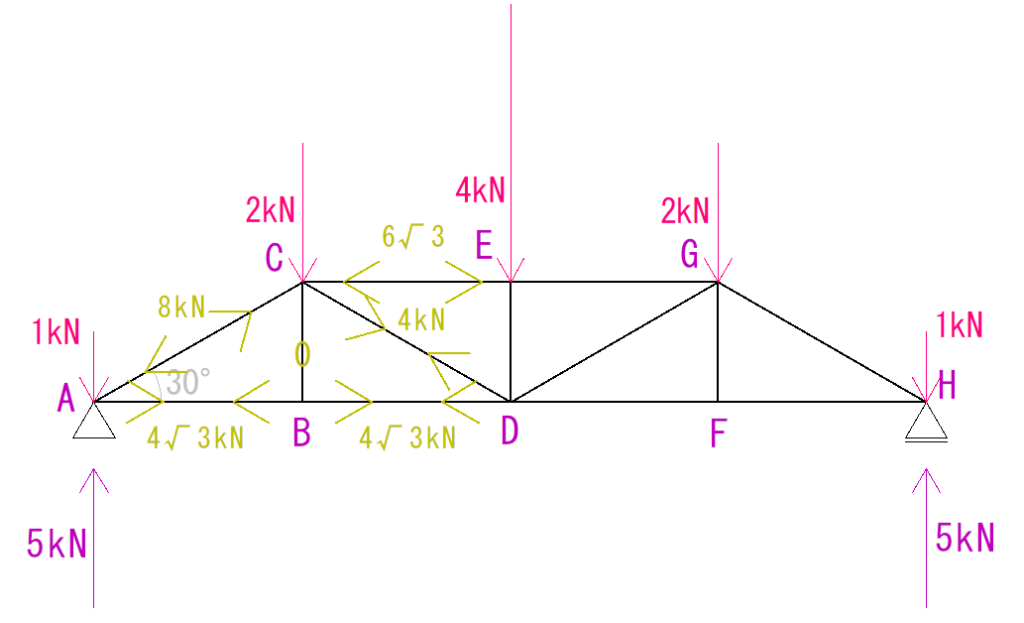
下の図のトラスを節点法の算式解法で解きなさい。
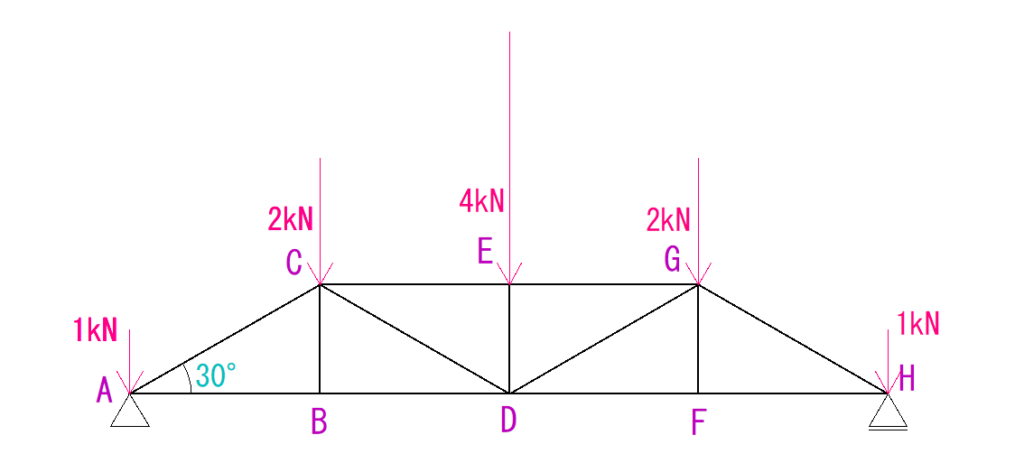
解説
考え方は図式解法の時と同じです。
一つ一つの節点を解いていきます。
この問題は、単純梁系トラスなので、まず反力を求めます。
反力の決定
このトラスは左右対称で、かかっている荷重も左右対称なので、総荷重の半分がVA、VBにかかるとわかります。
今回の総荷重は
1+2+4+2+1=10
これの半分なので
10÷2=5
VA=VB=5kN
となります。

A点の解法
まず、A点にかかっている荷重と反力を足します。
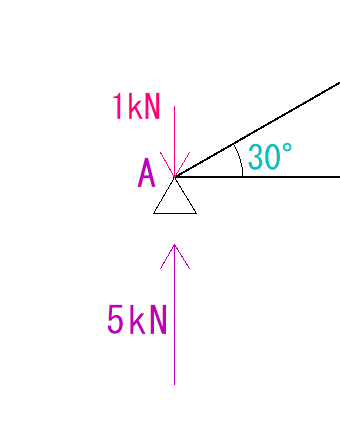
(-1)+5=4kN
そうしたら次に、部材を平行移動させた示力図を描きます。
ここは、精度が求められていないのでラフで大丈夫です。
(イメージするための図だと思ってください)
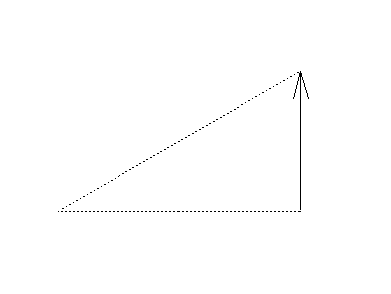
ここで矢印の向きが一周するように、矢印も書き入れてしまいます。
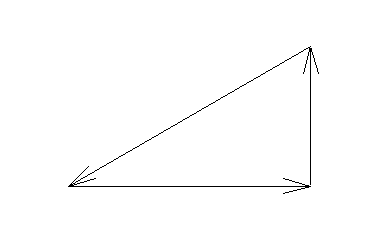
そうすると、良く見慣れた三角形が出てきました。
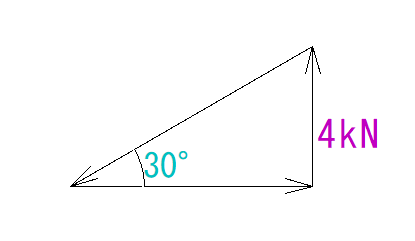
あとは1辺の長さを計算で出していきます。
三角関数が苦手な人は下のやり方がおすすめです。
補足:三角関数を使わず、比で求める方法
まず、この三角形の比を書き込みます。
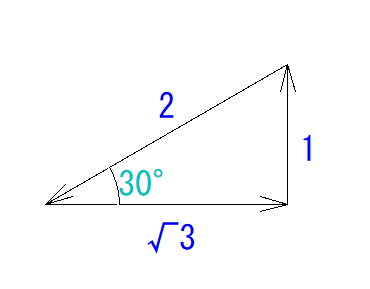
そうしたらわかっている数字を隣に入れます。
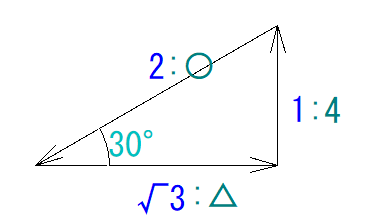
長さが知りたい辺を比の式で求めます。
1 : 4= 2 : 〇
〇 = 8
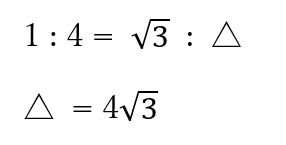
結構便利なので、やり方を覚えることをお勧めします。
B点の解法
このB点はトラスを解くうえでラッキー地点です。
重要な点ですが、
トラスのT字型部分は0が生じる
からです。
これはしっかり覚えておきましょう。
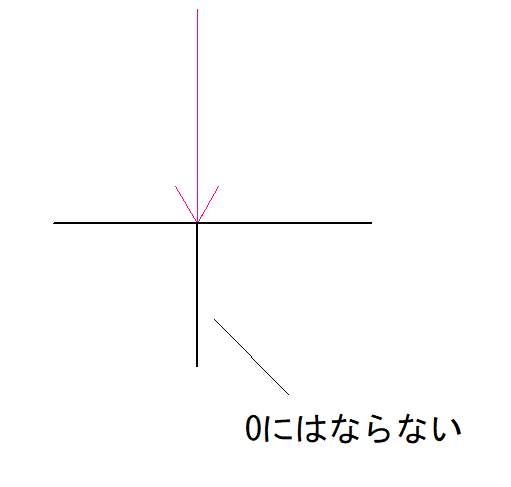
下の図のようなイメージです。
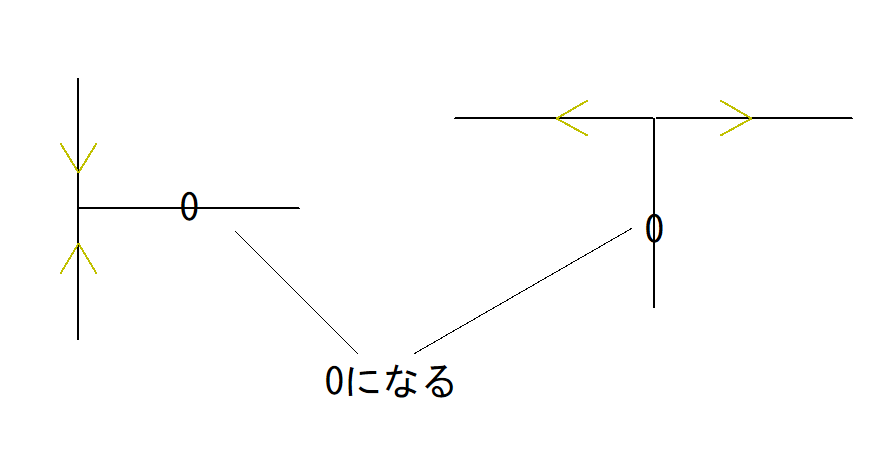
これはどんな大きさの力がかかっていたとしても成り立ちます。
ただ、荷重も含めてのT型なので注意してください。
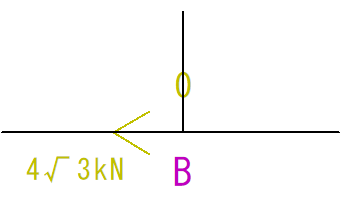
なので、B点は下の図のようになります。
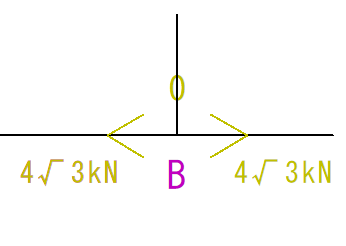
そうすると、右側の部材は、左側の部材の力と釣合うために、同じ大きさの力が反対方向に加わることが分かります。
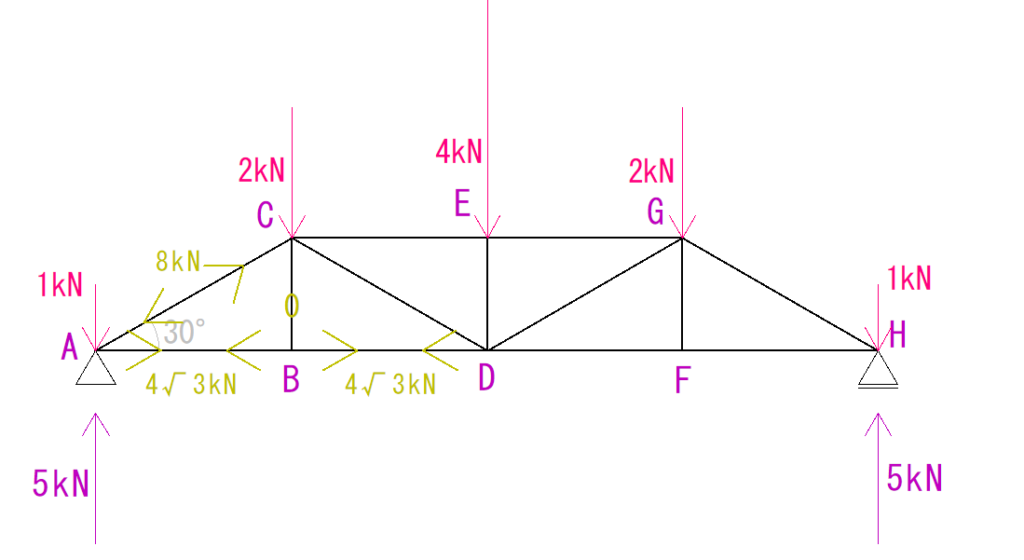
C点の解法
改めて基本部分の考え方に戻りますが、「節点法」というのは、各節点に加わっている力が釣合う、というものでした。
つまり、C点の
ΣX=0
ΣY=0
(ΣM=0 これは使いません)
ということになります。
では、それぞれを確認してみましょう。
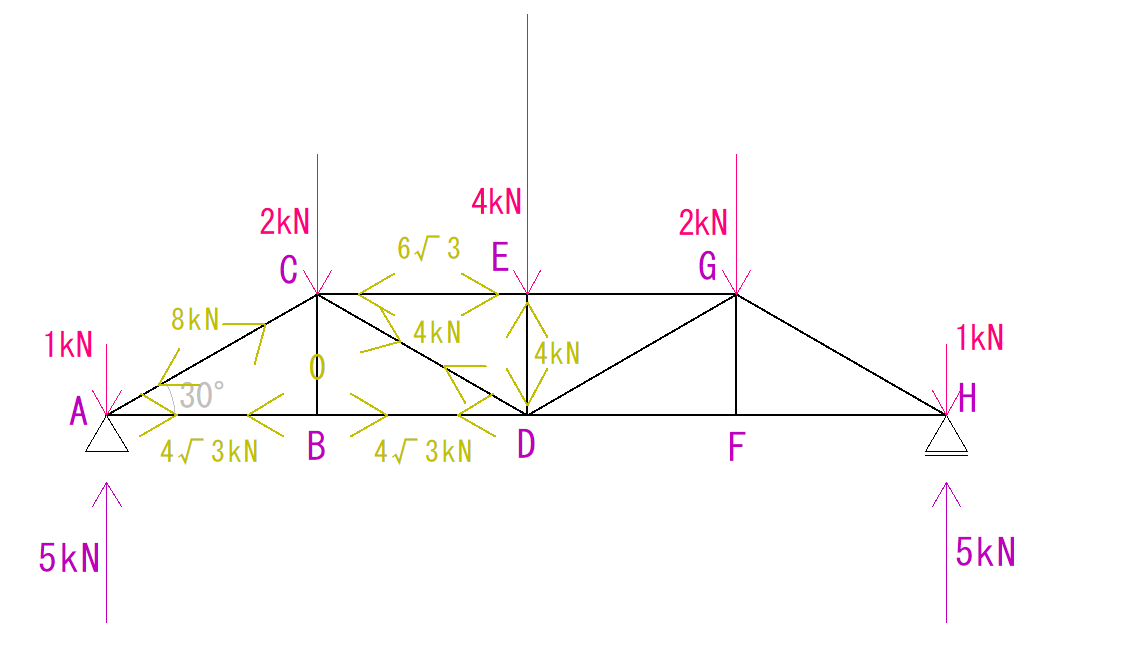
ΣX
分かっているのは30°の角度の8kNだけです。
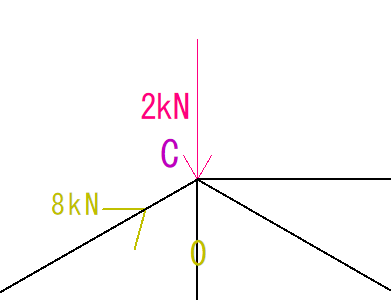
(荷重の2kNは垂直にかかっているのでX方向の計算には含めません)
この8kNをX方向とY方向に分解すると下の図のようになります。
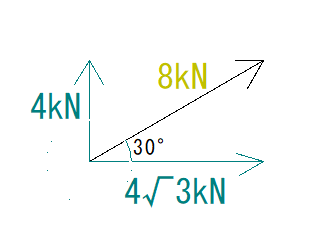
X方向で関係してくるのは4√3です。
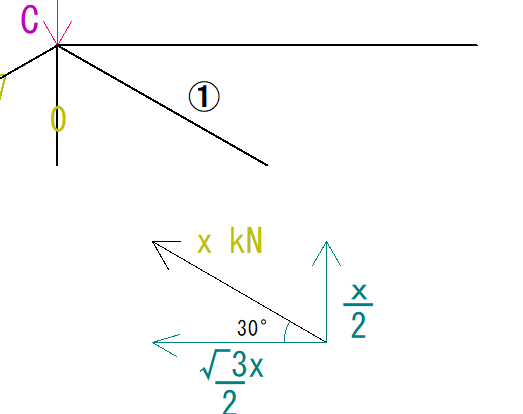
次に、①の部材にかかっている力をxとし、方向を仮定して、X方向とY方向の力に分解すると下の図のようになります。
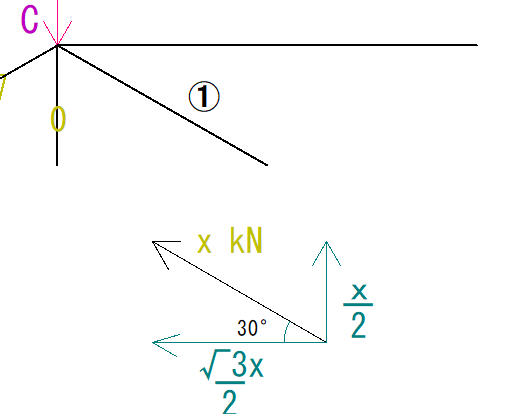
X方向にかかる力はー√3x/2(左向きなのでマイナス)となります。
最後②の部材はそのままX方向に向いているので、力の大きさはそのまんまです。
大きさはyとします。
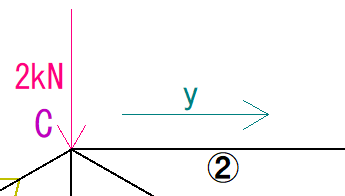
X方向の数値だけ出して、式にしていきます。
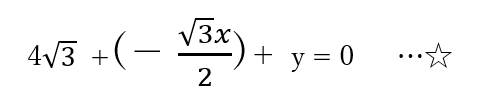
(マイナス方向に仮定した力には符号を忘れず書きましょう。)
ΣY
先程分解した8kNのY方向
①の部材のY方向の力
荷重の大きさ2kNを足していきます。
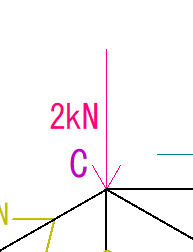
(②の部材はY方向への力は加えていないので計算に含めません)
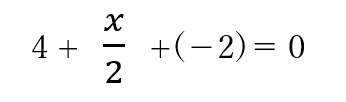
この式からxを求められます。
8 + x + -4 = 0
x = -4kN
このマイナスは、仮定した力が逆向きだったということを指します。
この答えから、①の部材にかかる力と向きが分かりました。
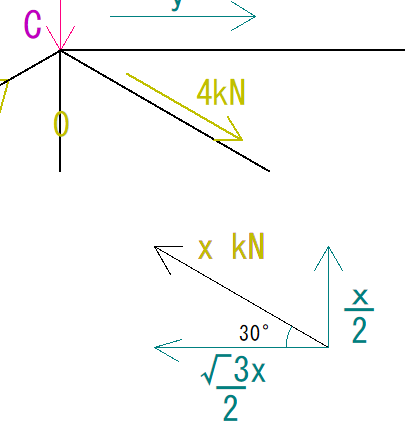
またΣXの時の式(☆マーク)に代入することで、②の部材の大きさも求めることができます。
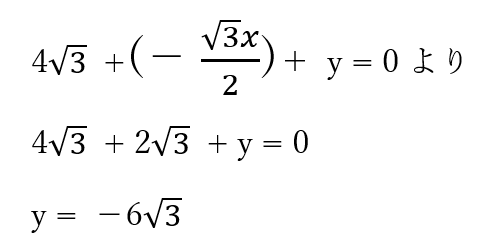
となります。
これも仮定とは逆向きになります。
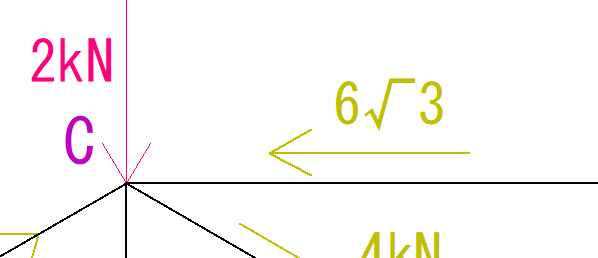
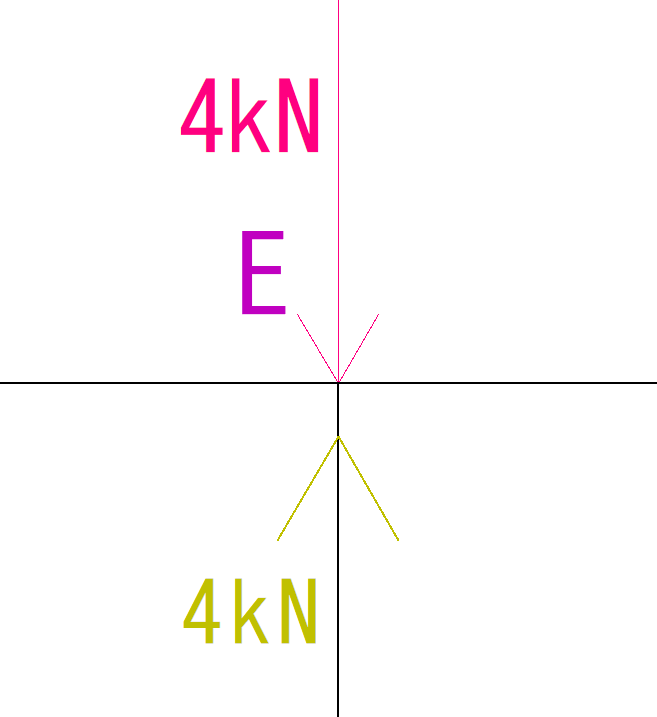
E点の解法
E点を解くうえで重要な点をもう一つ…
トラスの十字型の部分は左右上下が対象になる
という点です。
このことから、下の図のようになります。
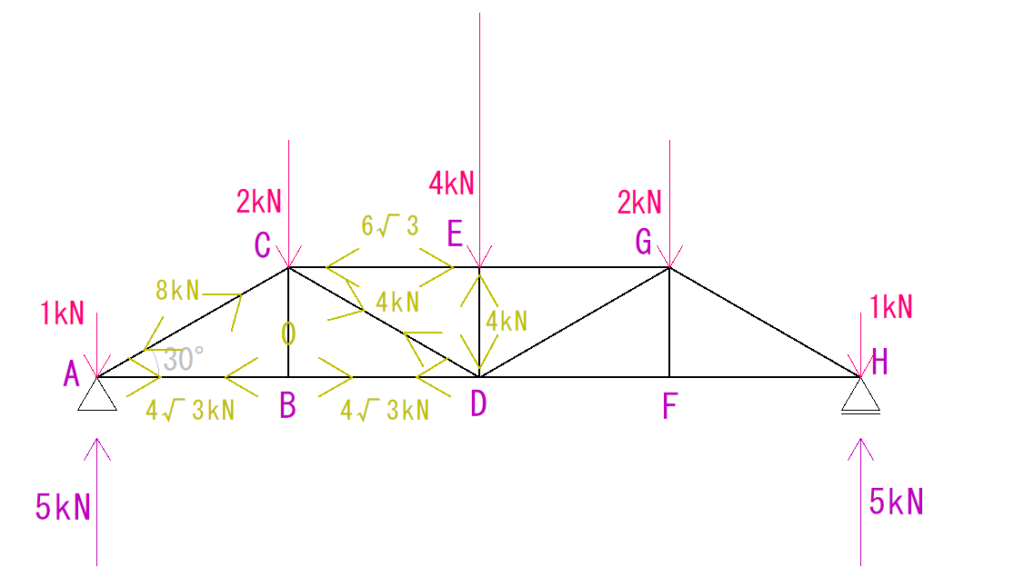
解答
このトラスは左右対称のため、片側の軸方向力を求めると、もう片方も分かります。
そのまま写してあげましょう。
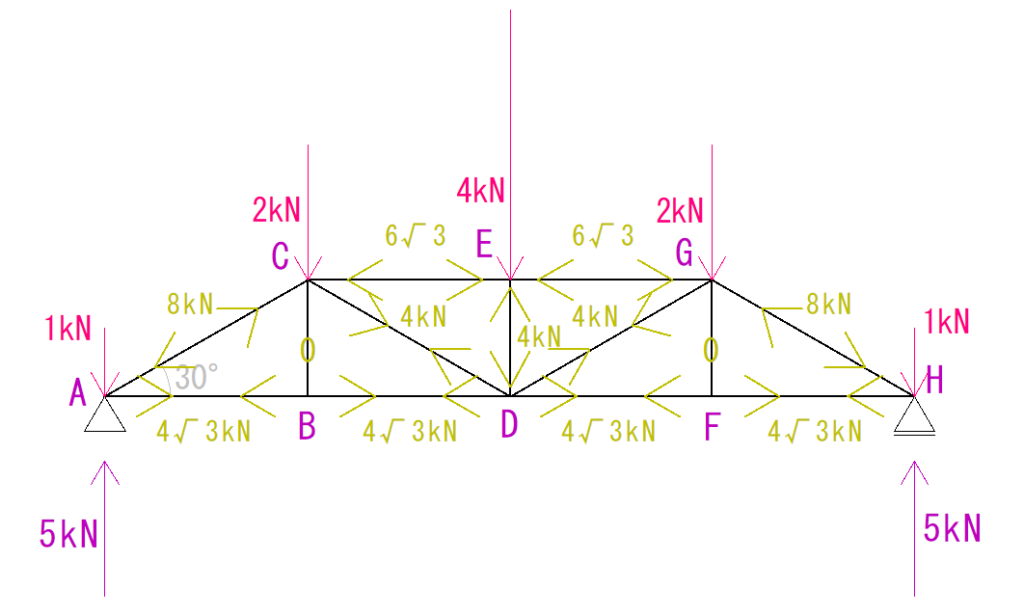
また、先生によっては「少数に直せ」という人もいるので、関数電卓などを用いて少数に戻すこともできます。
まとめ
この問題はC点でΣYを出したとき、きれいにxの値だけが出てきました。
しかし応用問題などになってくると、xだけの値が出てくるとは限りません。
そういう場合は、ΣXとΣYの式で連立方程式を立ててあげると、解くことができます。
トラスの「節点法」の算式解法は構造設計の分野でも難易度はかなり上位です。
一回では理解できないと思うので、繰り返し繰り返し練習して、分からないところがあったら先生や当サイトにご連絡ください。