先回は単純梁に1つの集中荷重がかかる場合の反力の求め方を解説しました。
まだ見ておられない方は下のリンクから見ることができます。
今回はその応用編として、単純梁に集中荷重が2つ以上かかった場合の反力の求め方を解説していきたいと思います。
例題
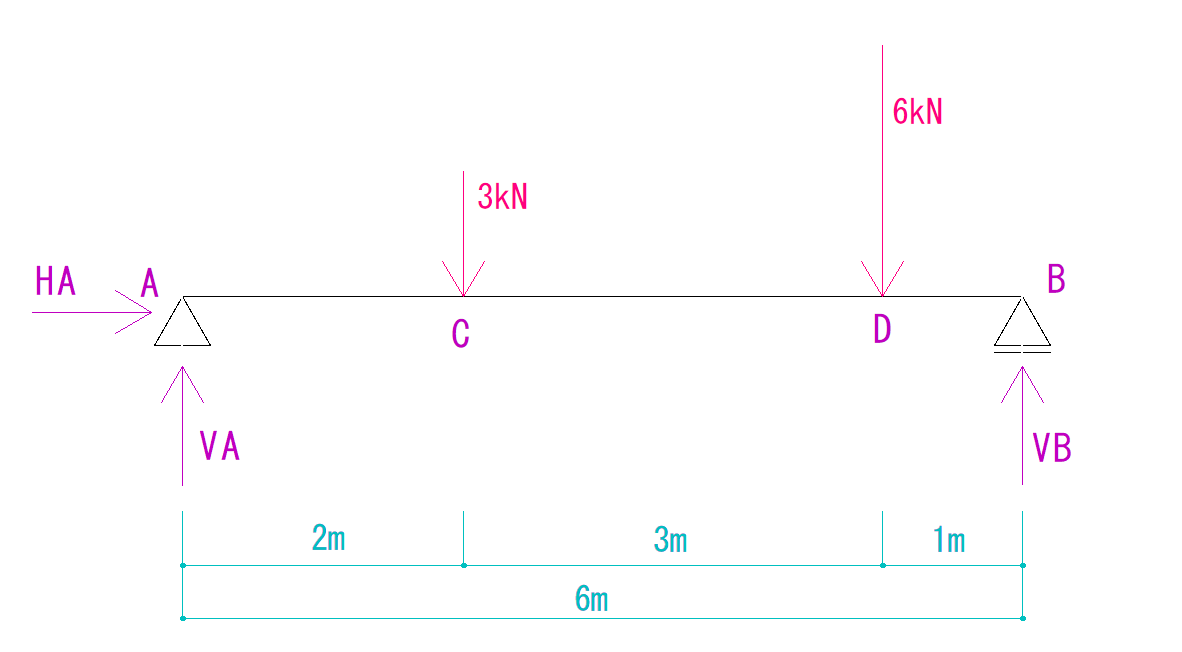
下の図を見て反力を求めなさい。
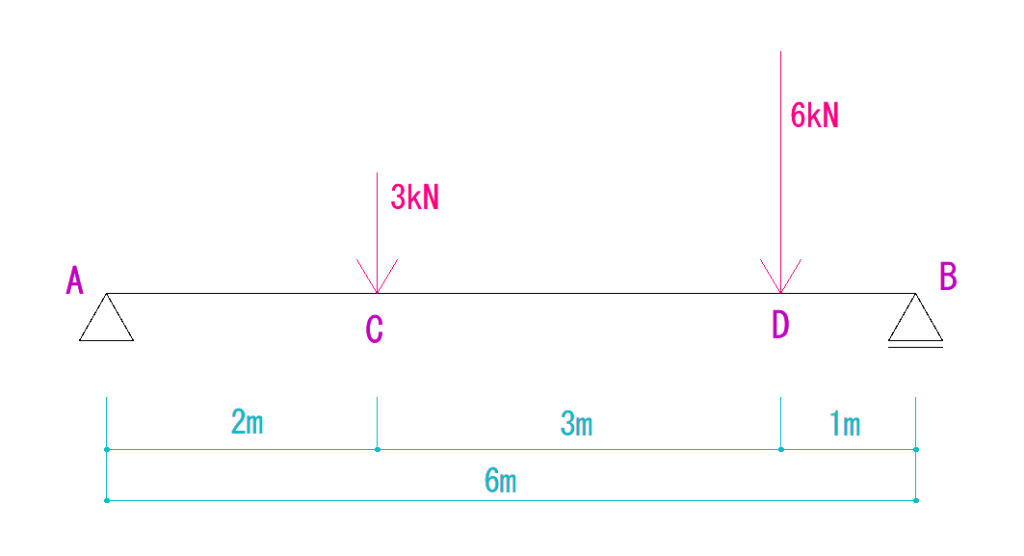
解説
反力の仮定
まず、それぞれの支点にどの種類の反力が、いくつかかるかを確認します。
これについては下のリンクの記事を参照ください。
この場合は下のように反力を仮定することができます。
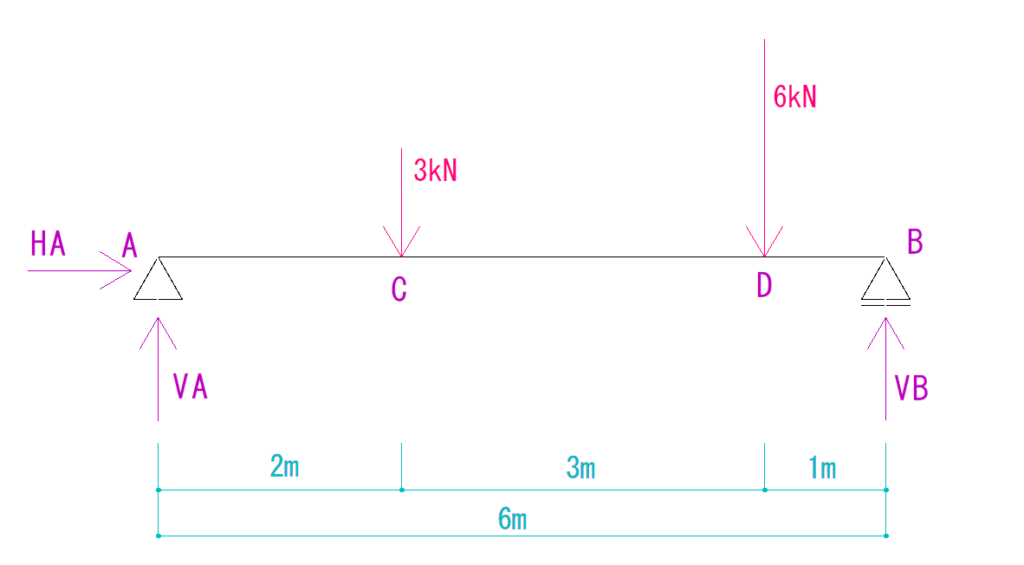
注意ですが、この時、反力の符号がプラス向きにするようにすることをおすすめします。
補足:力の符号について
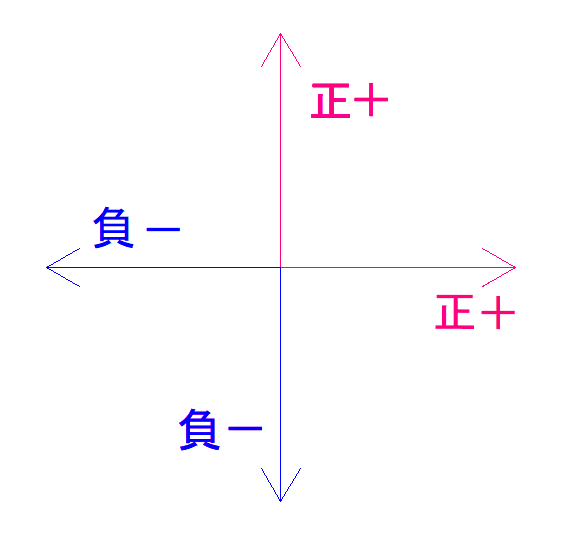
そうすると、これから式を立てるとき符号ミスが減ります。
(明らかにマイナスの向きにかかる場合は、仮定でマイナス向きにしてもいいですが、符号は間違えないようにしましょう。)
では、問題を解いていきます。
2つ以上の力がかかる場合の解き方
単純梁に2つ以上の力がかかる場合、やり方としては二つあります。
一つは、それぞれに分解して考える。
二つ目は、合力を求めて考える。
というものです。
では、それぞれの解き方を考えていきます。
自分がやりやすい方で覚えましょう。
1.それぞれに分解して考える
この方法は少し計算量が増えるかもしれませんが、一つ一つの計算は簡単なのでミスは少ないかと思います。
まず、下の図のように分けて考えます。
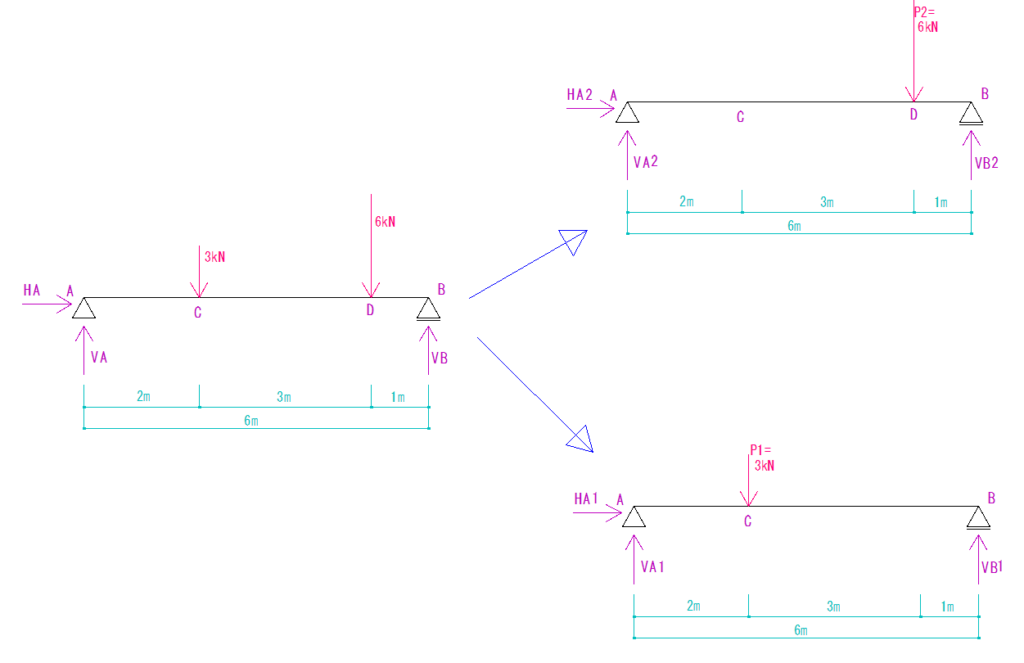
こうすると、一つ一つは先回やった単純梁に1つの集中荷重がかかった場合になるので解くことができます。
ここでは詳しく解説しないので、詳しく知りたい方は下のリンクからやり方を確認してください。
P1の式
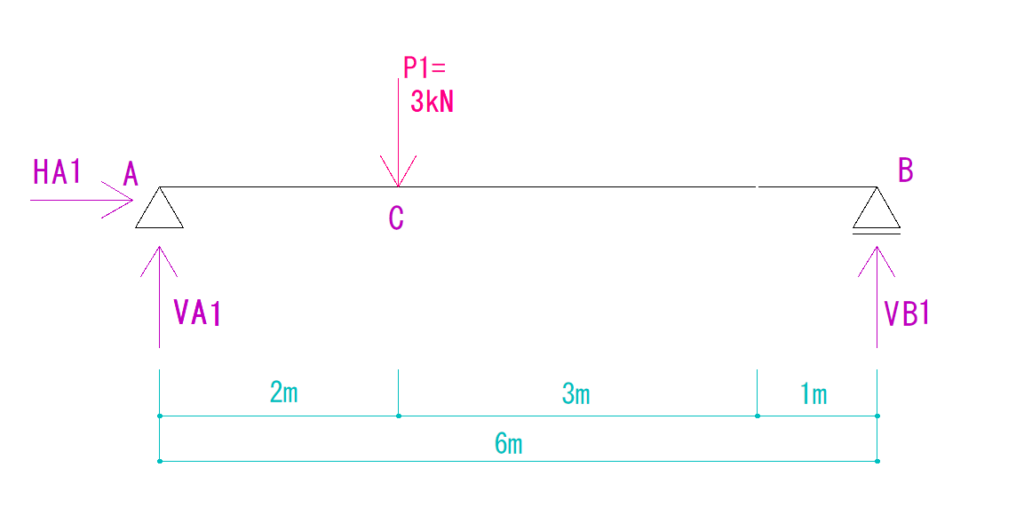
HAは省略
ΣMA=0より、
(-3kN×2m) + VB1×6m=0
VB1=1kN(仮定通り上向き)
ΣY=0より、
VA1+1kN+(-3kN)=0
VA1=2kN(仮定通り上向き)
P2の式
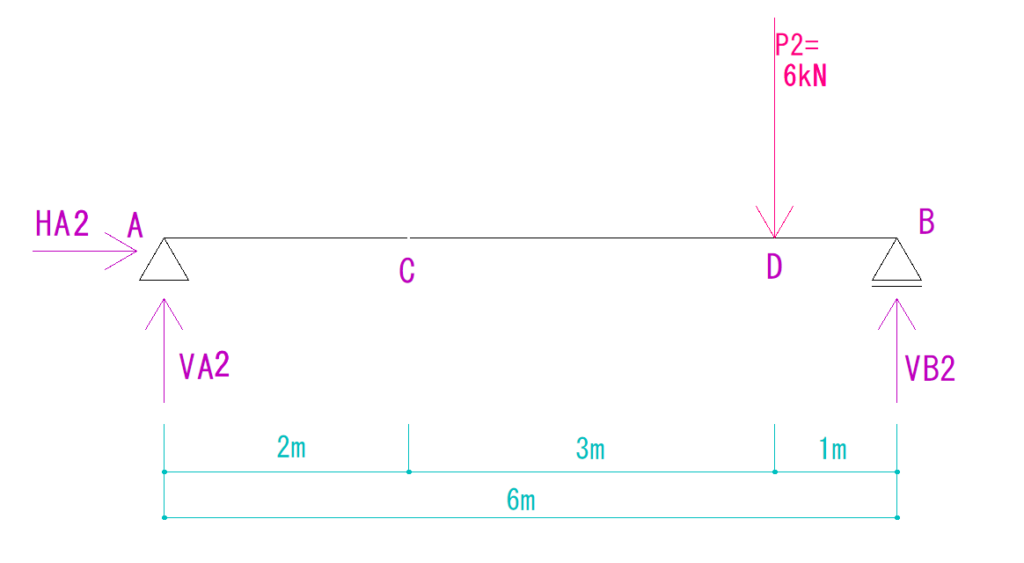
HAは省略
ΣMA=0より、
(-6kN×5m) + VB2×6m=0
VB2=5kN(仮定通り上向き)
ΣY=0より、
VA2+5kN+(-6kN)=0
VA2=1kN(仮定通り上向き)
そうしたら、それぞれのVA,VBを足してあげます。
VA1+VA2
=2kN+1kN
=3kN
VB2+VB2
=1kN+5kN
=6kN
どちらも符号がプラスなので答えも上向きと分かります。
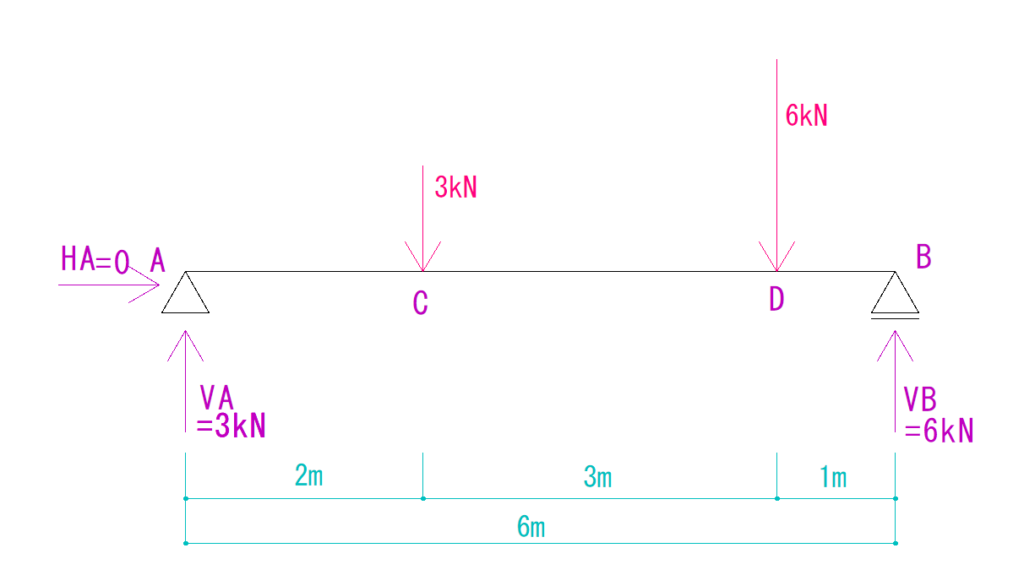
答え
HA=0
VA=3kN(仮定通り上向き)
VB=6kN(仮定通り上向き)
となります。
合力を求めて考える
まず、2力の合力を求めます。
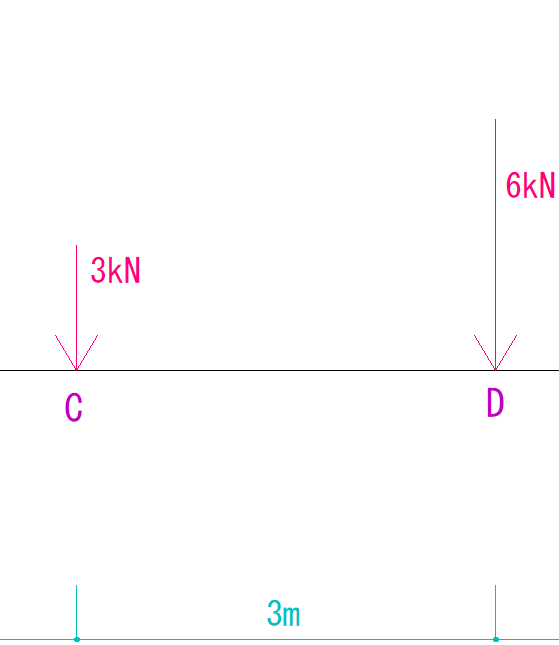
これは平行な2力の合成なので、バリニオンの定理を使うと簡単に求めることができます。
ここでは合成方法はさらっと行きたいと思います。
詳しいやり方は上の記事をご覧ください。
バリニオンの定理より、
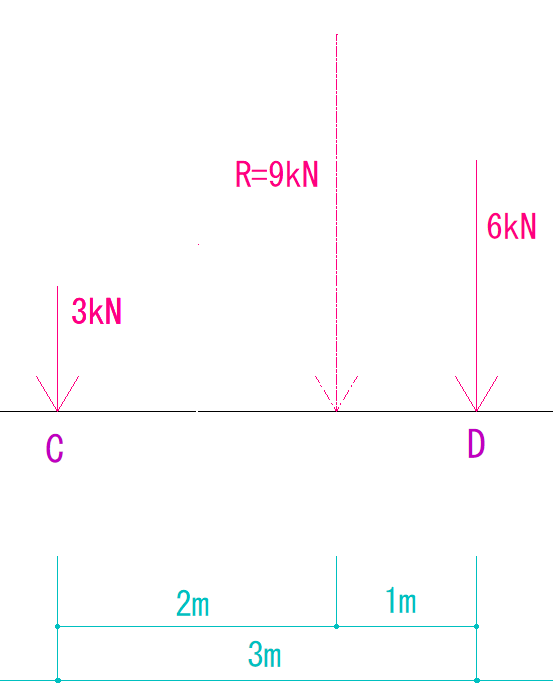
点OをP1(3kN)の作用線上に仮定します。
P2(6kN)がO点を回す力と合力R(3kN+6kN=9kN)が回す力は等しくなるので、
6kN × 3m = 9kN × r m
r = 2m
となります。
あとは先回やった、単純梁に1つの集中荷重がかかった場合の反力の求め方で解いていくことができます。
詳しくは下の記事をご覧ください。
Rの式
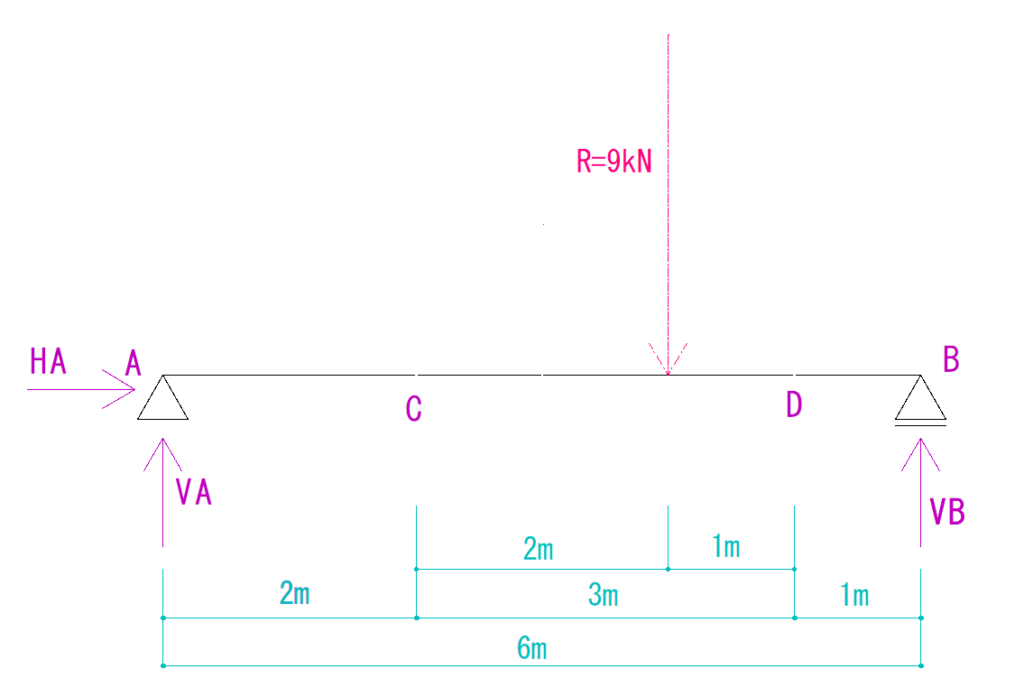
HAは省略
ΣMA=0より、
(-9kN×4m) + VB×6m=0
VB=6kN(仮定通り上向き)
ΣY=0より、
VA+6kN+(-9kN)=0
VA=3kN(仮定通り上向き)
となります。
答え
HA=0
VA=3kN(仮定通り上向き)
VB=6kN(仮定通り上向き)
となります。