今回は反力について解説していきたいと思います。
さて、反力ですが、これからとても大切になってきます。
問題を解くごとに「反力を求めなさい」というのが出てくるかと思いますので、しっかりと理解しましょう。
反力とは?
反力とはなんなのか。
反力→反する力
…っとそのまんまですね。
もう少し詳しく説明しましょう。
壁を押しているところをイメージしてください。
もちろん壁はピクリとも動きません。
壁に押し返されているからです。
押した分の力と同じ力で押し返されています。

そのため壁は動かないのです。
この、壁から押し返される力を反力と言います。
かけた力が反力より大きくなれば物は壊れます。
では、反力をどうやって求められるのか…
反力とは新しい単語ですが、実はもうすでに勉強した分野の言い換えなんです。
それは、
「力の釣合い」
です。
「反力」=「力の釣合い」
と覚えておいてください。
つまり、問題で「この力の反力を求めなさい」というものが出たら、つまりは「この力に釣合う力を求めなさい」ということです。
力の釣合いについては下のリンクから詳しく見ることができます。
「あいつとこいつは釣合っている…?皆さん、力の話です。力の釣合いについて解説!」
「作用点の違う力の釣合いについて解説!釣合うには回ってもいけません!算式解法」
「作用点の違う力の釣合いについて解説!釣合うには回ってもいけません!図式解法」
しかし、考え方としては一緒ですが、問題の解き方は少し変わります。
条件が少し増える感じです。
そこを理解するために、まずは「支点」について理解しましょう。
支点の種類
支点には3つの種類があります。
下の図を見て確認しましょう。
移動支点(ローラー支点)

・水平移動=してしまう
・垂直移動=しない
・回転 =してしまう
支えられる反力は1方向
回転支点(ピン支点)

・水平移動=しない
・垂直移動=しない
・回転 =してしまう
支えられる反力は2方向
固定支点(固定端)

・水平移動=しない
・垂直移動=しない
・回転 =しない
支えられる反力は3方向
支点なのに水平移動「してしまう」ってどういうことだよ!って思いませんか?
ちなみに学生時代、私は思いました。
これは書き方が悪いのですが、支点は基本的に動きません。
水平移動する支点だからと言って、ちょっとの力でコロコロ動くようなものではありません。
安心してください。
ただ、大きな力がかかったときに、耐える力がある支点と、ない支点があるということです。
加えて、支えられる反力の数をしっかりと覚えておきましょう。
ここは基礎の分野になります。
さて反力は、この支点の支えられる能力に従って釣合う力を求めていきます。
では、例題から考えていきましょう。
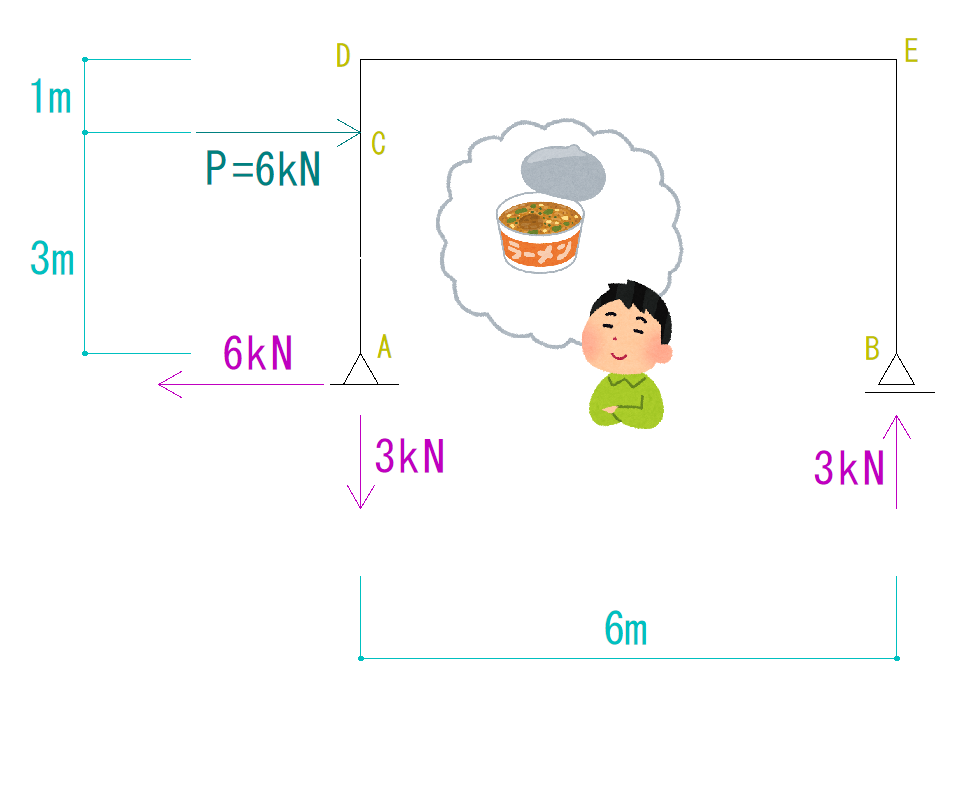
例題
下の図を見て支点A,Bに生じる反力を算式解法で求めなさい。

解説
まずは、それぞれの支点の反力を仮定として書き込みます。
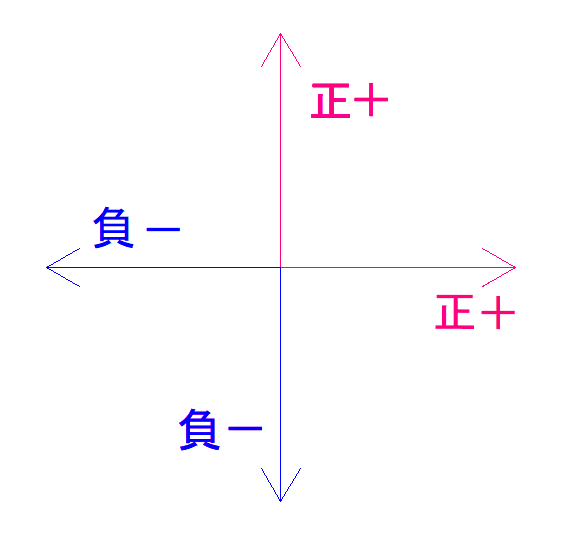
この時、反力は+向きに仮定するようにしましょう。
参照

力の釣合い条件を一つずつ考えていきます。
確認です。
力の釣合い条件3つ
ΣM=0
ΣX=0
ΣY=0
です。
まず、ΣXを考えます。
問題を見ると、荷重はX方向への力をかけていません。
よって
HA+0=0
HA=0
となります。
あとは、力の釣合い条件で解くことができます。
単純梁に集中荷重がかかった場合の反力の求め方について詳しくは下の記事を参照
A点をO点と仮定し、荷重のモーメント力とVBのモーメント力を釣合わせます。
(6×4)-(VB×6)=0 (VBはO点を反時計回りに回す、と仮定しているため符号は-)
24=6VB
VB=4kN(仮定通り上向き)
ΣY=0より
VA+4+(-6)=0
VA=2kN(仮定通り上向き)
解答のまとめ
HA=0
VA=2kN(上向き)
VB=4kN(上向き)
となります。
反力は、新しい分野というより、これまでやったことの復習という感じでした。
パニックにならず、しっかりと問題を解けるようになりましょう!