さて、先回は反力とはなにか、ということを考えることができました。
まだ見ておられない方は下のリンクから見ることができます。
今回は片持梁とラーメン構造の時の、反力の求め方について解説していきたいと思います。
片持梁の反力を求めてみよう
片持梁とは
まず、片持梁とは何かを理解しましょう。
図で表すと下のようになります。

片方は何も支点がなく、もう片方は固定支点(固定端)でがっちりと止まっています。
これはバルコニーを想像しましょう。

バルコニーの断面図だと思うと、問題をイメージしやすいと思います。
もちろん強度はそこそこありますが、張り出しの部分が大きくなればなるほど、モーメント力(支点を回す力)が大きくなっていきます。
今後、片持梁はよく出てくるのでしっかりと理解しておきましょう。
片持梁の反力の解説
では例題から考えていきましょう。
例題
下の図を見て反力を求めなさい。

解説
まずは下の図のように反力を仮定します。
(水平力は生じていないので水平反力も0ということで、割愛します)
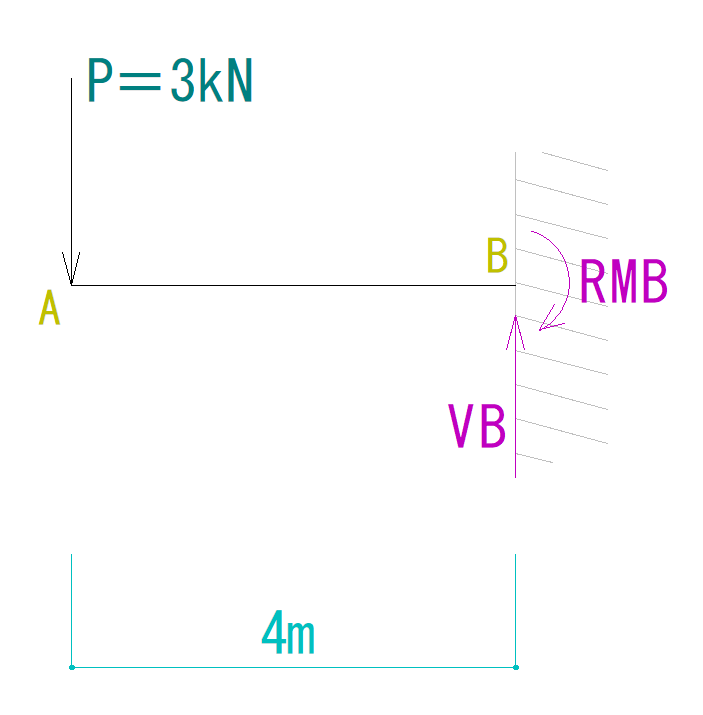
力の釣合い条件から
ΣY=0より
(-3kN)+VB=0
VB=3kN(上向き)
ΣMB(B点におけるモーメント力の総力)=0より
-(3×4)+RMB=0
なぜ最初にマイナスが付いているかというと、PはB点を反時計回りに回すためです。
そして式を計算すると
RMB=12kN・m(時計回り)
となります。
補足:モーメントの反力とは?
ここで出てきたのですが、モーメントの反力について少し解説したいと思います。
垂直な力や水平な力の反力はイメージしやすいですよね。
壁を押して時に押し返される力です。
では、モーメント力の反力とはなんでしょうか?
以前考えたようにモーメントとは、回す力です。
(まだ見ておられない方は下のリンクを参照)
そこでドアをイメージしてみてください。
鍵が付いていないドアのある部屋にいます。
その部屋に勝手に入ろうとしてくる人がいます。
あなたは入ってほしくありません。
でも鍵がないので、ドアノブを手で回らないように押さえます。

その時、相手が回そうとする方向とは反対方向に回す力を加えます。
そうすると力が釣合い、ドアノブは回りません。
これがモーメント力の反力です。
つまり、モーメント力の反力とは、回ろうとする方向と反対方向にかかる力です。
なんとなく理解できたでしょうか?
ラーメン構造の反力を求めよう
ここでも簡単に説明しますが、下のリンクの記事ではさらに詳しく解説しています。
ラーメン構造とは
ラーメン構造…と最初出てきたとき何か思い浮かべませんでしたか?
…ちなみに私はラーメンを食べたくなりました。

もちろんラーメン構造のラーメンとは、食べるラーメンではありません。
調べたところ、ドイツ語からきているようです。
くれぐれも授業中にお腹の虫がならないようにお気をつけて…
さて、ラーメン構造とはどういう構造なのかを簡単に理解しましょう。
Wikipedia先生には、こう書いてありました。
ラーメン (独: Rahmen) とは構造形式のひとつで、長方形に組まれた骨組み(部材)の各接合箇所を剛接合したものをいう。ドイツ語で「額縁」の意。建築・土木構造の分野では柱が梁と剛接合している構造をラーメン構造という。
Wikipedia 「ラーメン(骨組)」
…建築を勉強している方ならなんとなく内容は理解できるでしょうか?
簡単に言うと、柱と梁がガッチガチにつけられている構造物のことです。
このガッチガチっていうのは、木で組んだとか、そういうものではありません。
溶接して、どうやっても分離させるのが難しいものです。
ラーメン構造の場合、やはり構造設計も変わってきます。
柱と梁の部分を継ぎ目とせずに一体の物として計算するのです。
ラーメン構造の分野もこれからよく出てきます。
しっかりと理解しておきましょう。
ラーメン構造の反力の解説
では例題から考えていきましょう。
例題
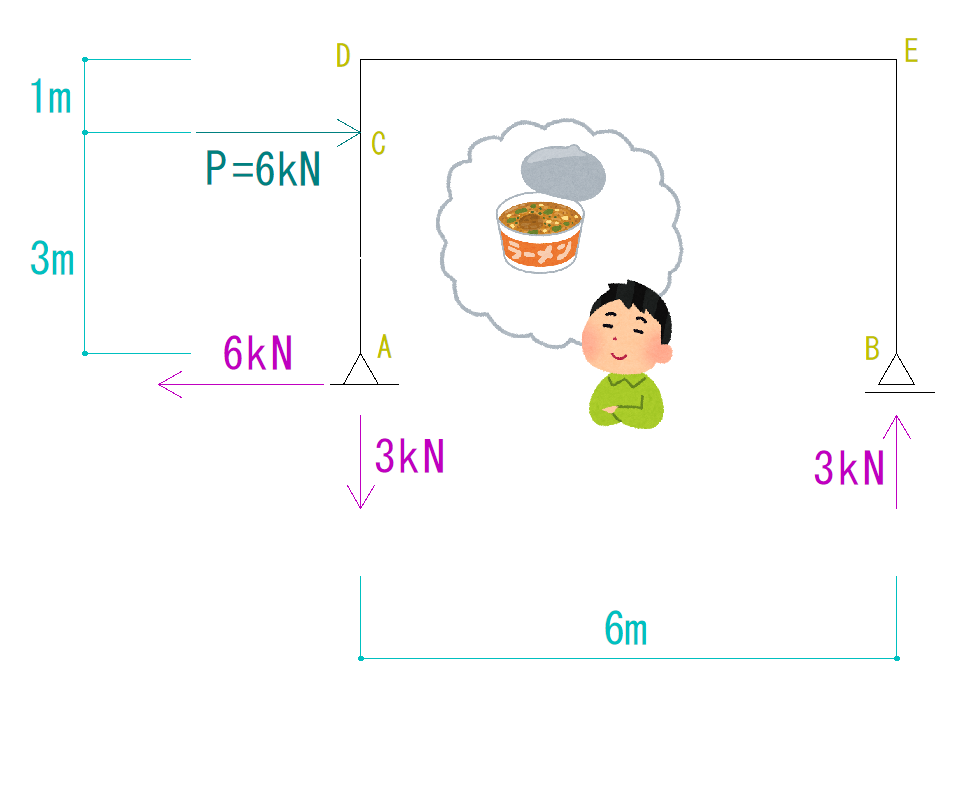
下の図を見て反力を求めなさい。

解答
まずは下の図のように反力を仮定します。

力の釣合い条件から
ΣX=0より
6+HA=0
HA=-6kN
HA=6kN(左向き)
ここで注意ですが、計算の結果符号がマイナスになる場合、仮定とは反対方向の向きになります。
注意しましょう。
…さて、これで終わろうとしていませんか?
実は、まだ終わりません!
この問題のPは、横に押すだけではなく、回す力も持っているんです!
想像してみてください。
箱を地面に近いところと、上の方で反対方向に押すと、コロッと倒れます。
もう少し丁寧な言い方をすると、回転する力が生まれたために、倒れます。

同じような原理でモーメント力が発生してしまうのです。
頭のいい方ならわかるかと思いますが、問題のここの部分、

実は、偶力になっています。
そのため、この回転する力と同じ大きさの力で、逆向きに作用する反力が必要となります。
…どうするか、
一つずつ考えていくと簡単です。
やっていきましょう。
まず、A点を基準にします。(B点でも可)
力が釣合っている状態とは、どの部分でもモーメントの総和は0になっているということです。
ということは、
RMA=0です。
A点を回す力を、一つずつ求めていきます。
VA×0(おなじA点に作用するため距離は0)
+6kN×0(おなじA点に作用するため距離は0)
+6kN×3m(PがA点を回す力)
+(-VB×6m(仮定のVBがA点を反時計回りに回すためマイナス))
=0
モーメント力が0のものを除外すると下の式になります。
6kN×3m+(-VB×6m)=0
VB=3kN(上向き)
となります。
ただ、これだけではΣYが0になりません。
最後に
ΣY=0より
VA+3kN=0
VA=-3kN(符号がマイナスということは、仮定とは逆向き)
VA=3kN(下向き)
となります。
答をまとめると、
HA=6kN(左向き)
VB=3kN(上向き)
VA=3kN(下向き)
となります。

しっかりと理解しておきましょう。