今回は3ピン式のラーメン構造の反力の解き方の計算方法(算式解法)について解説していきたいと思います。
3ピン式のラーメンについては先回の記事で解説しておりますのでそちらでご確認ください。
例題
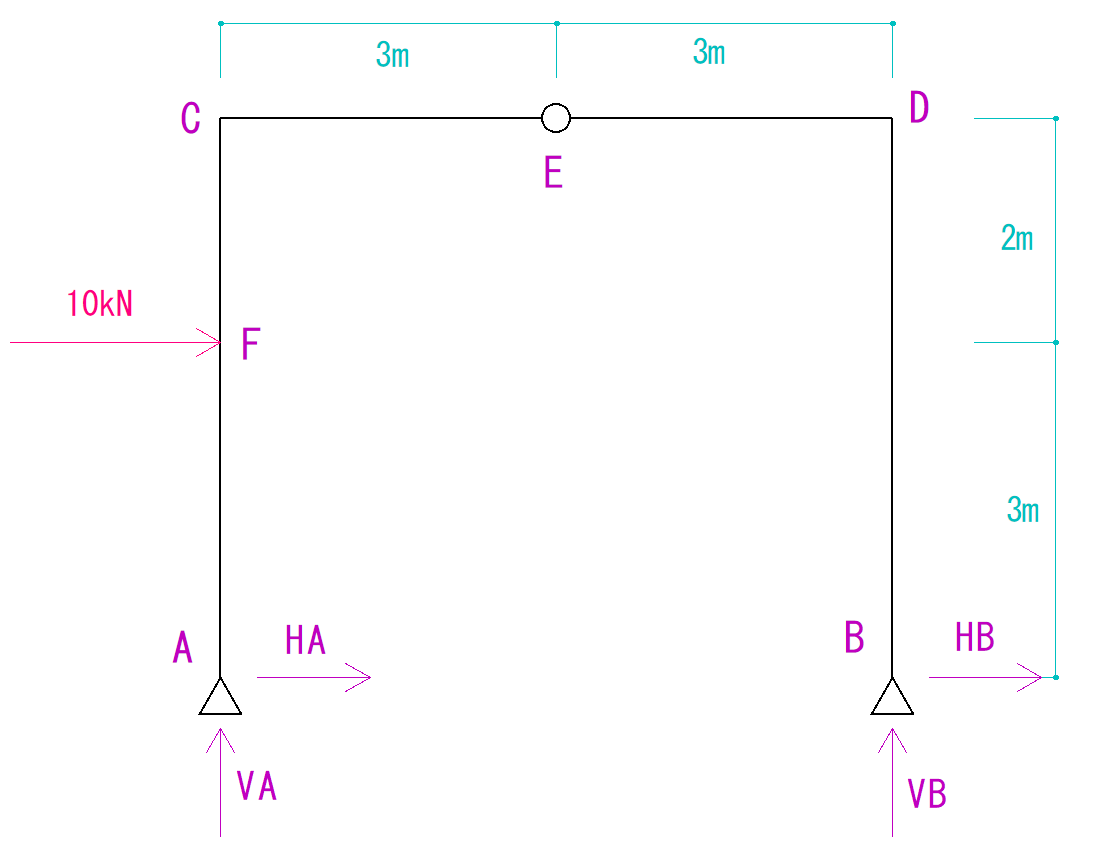
下の図を見て支点にかかるそれぞれの反力を求めなさい。
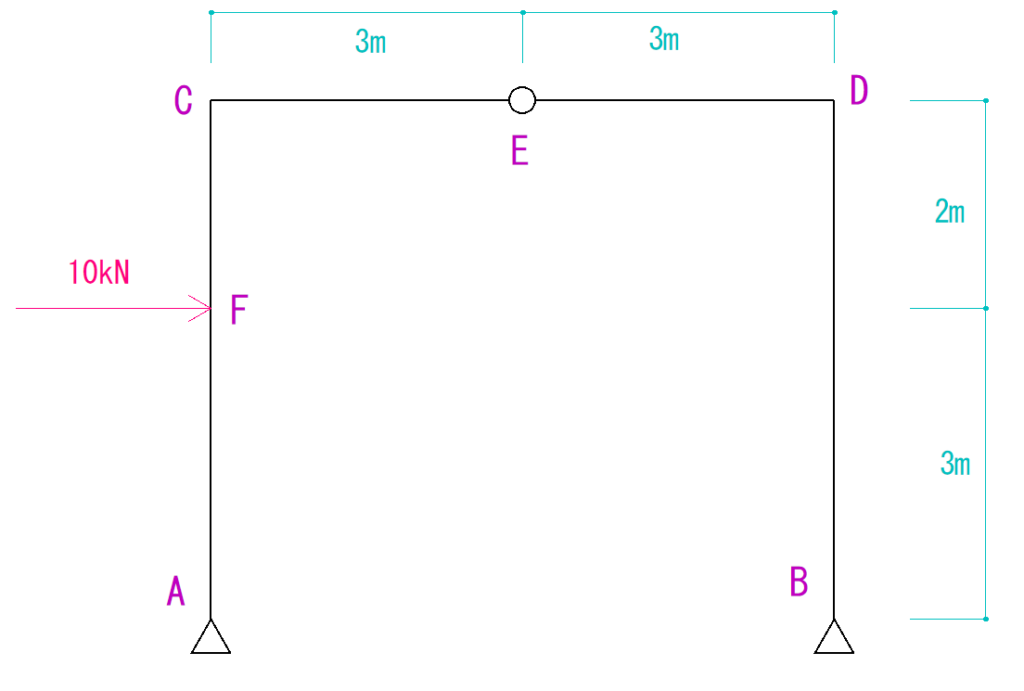
解説
反力の仮定
まずはこれまで通り反力を仮定していきます。
確認ですが3ピン式のラーメン構造は反力が4つ生じます。
それぞれをプラス方向の向きで仮定しましょう。
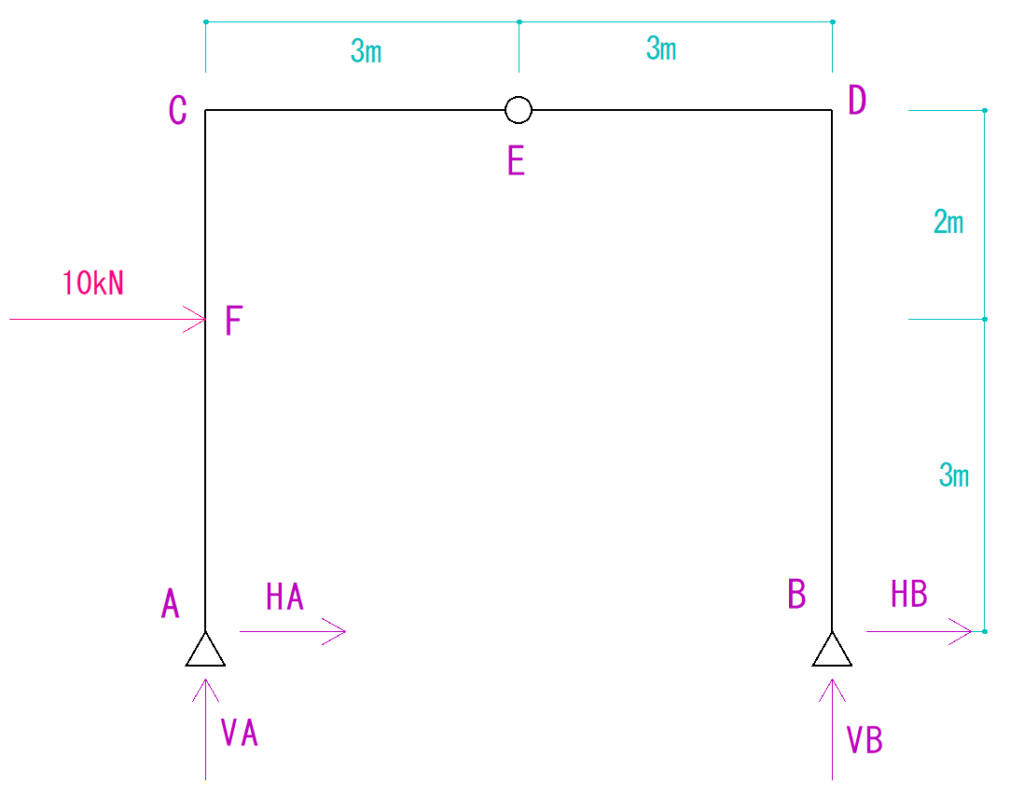
こうしたら3ピン式のラーメン構造の釣合い条件から一つずつ考えていきます。
ΣX=0
ΣY=0
ΣMo=0
「ピン節点」の地点のM値=0
の連立方程式で解くことができます。
ΣX=0
まずはX方向にかかっている力だけを見てみます。
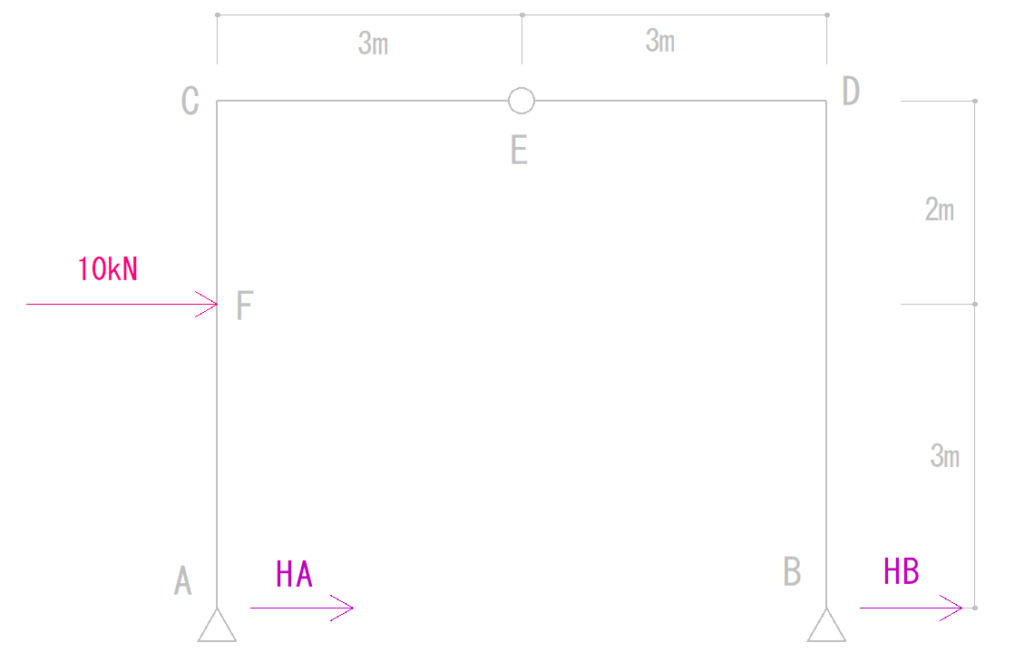
上の図を式にすると
10kN + HA + HB = 0 …①
となります。
これ以上計算できないので次に進みます。
ΣY=0
次にY方向にかかっている力を見ます。
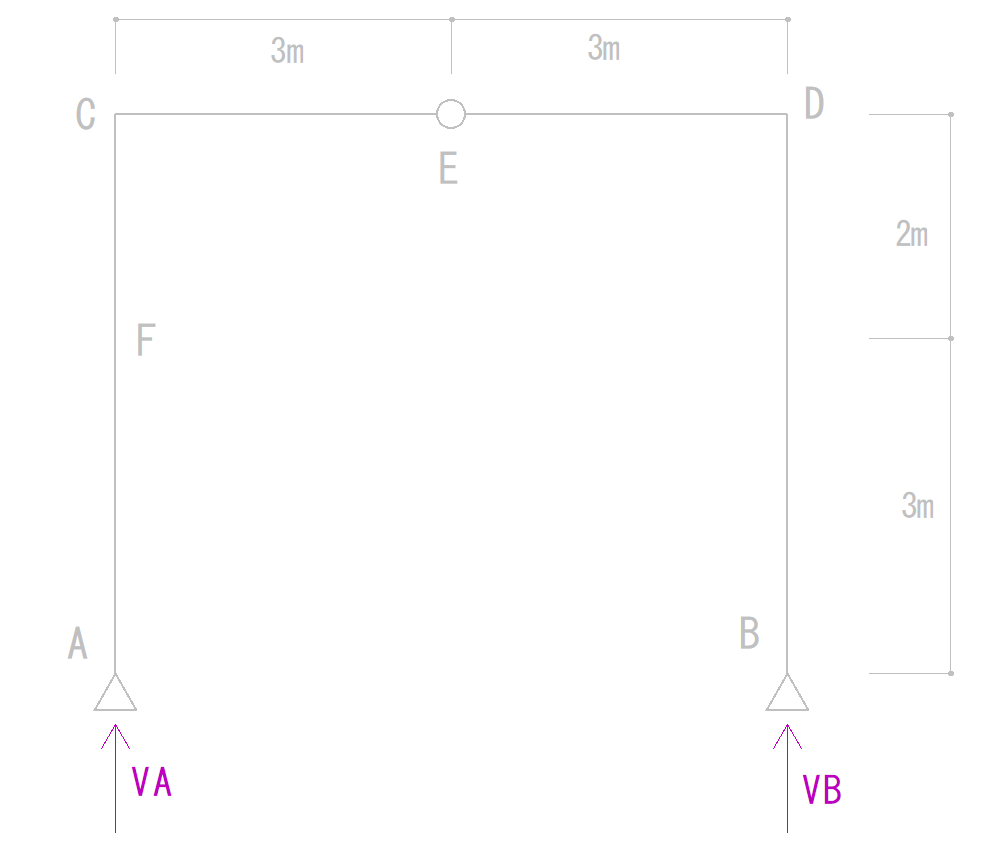
上の図を式にすると
VA + VB = 0 …②
となります。
これ以上計算できないので次に進みます。
ΣMo=0
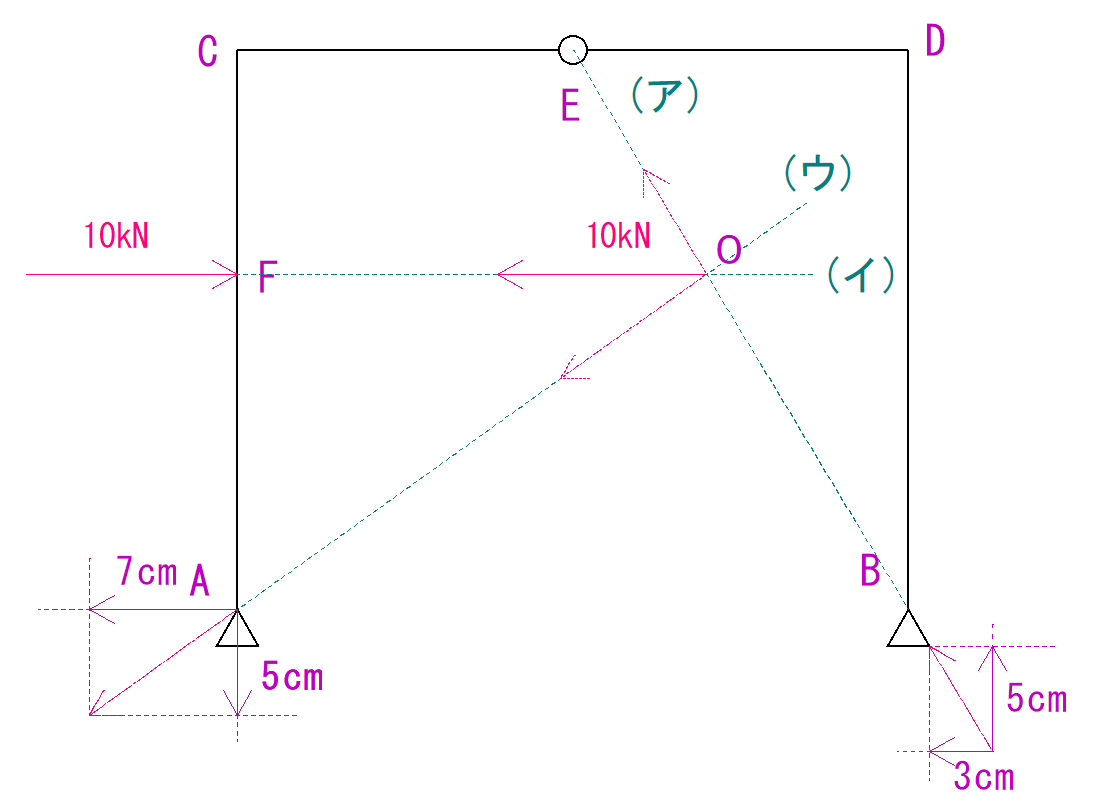
o点というのは任意点なのでどこにとってもいいということです。
基本的に、式を簡単にするため支点に取ることが多いです。
今回も支点であるB点にo点を取りたいと思います。
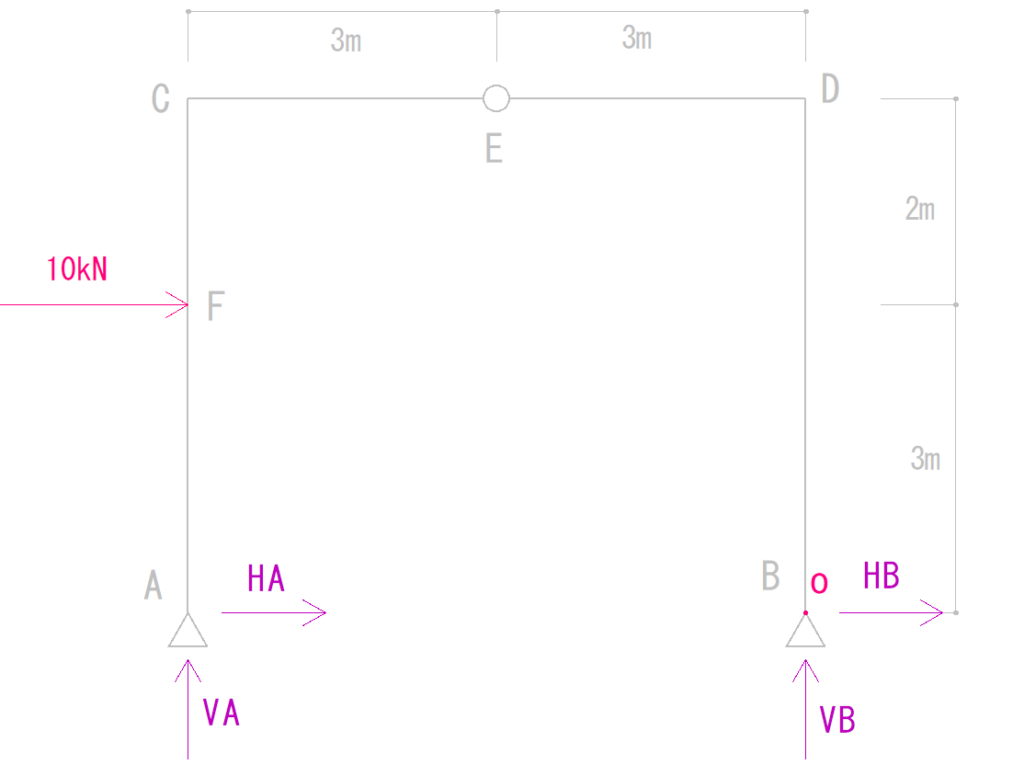
それぞれの力がo点を回す力を計算していきます。
(HA,HB,VBは力の作用線とo点の垂直距離が0なのでモーメント力も0になります。
式ではその部分を割愛します。)
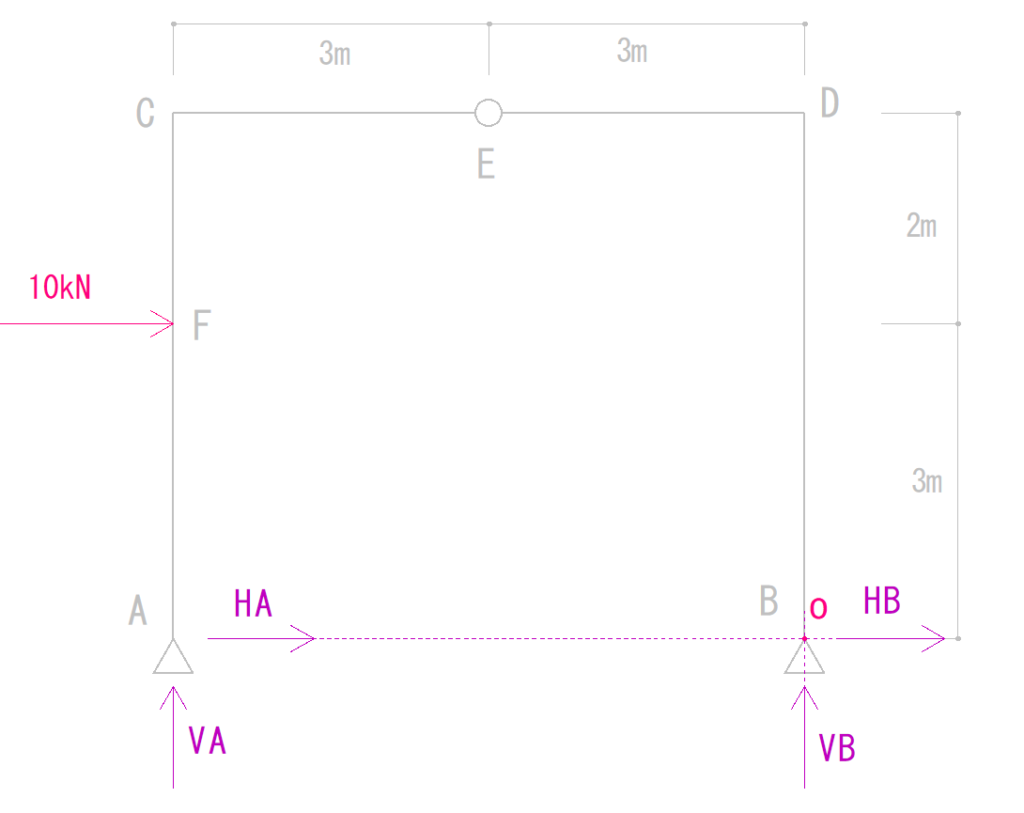
o点を回す力はVAと荷重の10kNのみです。
それを式にすると
VA × 6m + 10kN × 3m = 0
6VA = -30
VA = -5kN …③
符号がマイナスになったということは仮定とは逆向きということになります。
「ピン節点」の地点のM値=0 (ME=0)
さて問題はここです。
「ピン節点」の地点のM値はどのように計算すればよいのでしょうか?
やり方は簡単です。
1.片手を用意して、「ピン節点」より右側(左側でも可)を隠します。
2.隠れていない方の荷重のE点を回す力の総和を求めます。
3.それが0になるようにします。
実際にやってみましょう。
まずは「ピン節点」より右側を隠します。(左側のみを見ます)
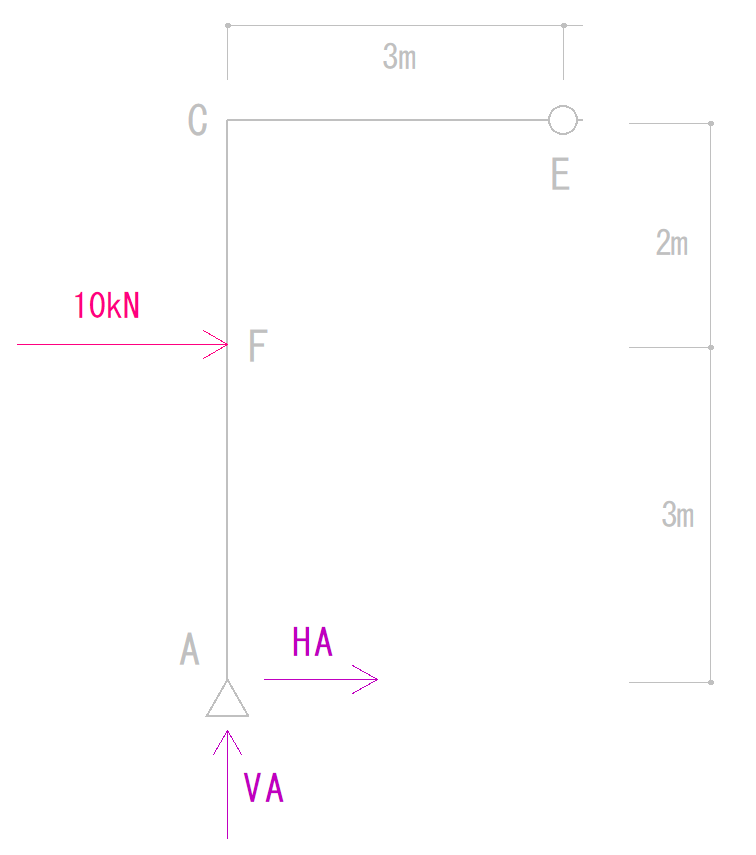
それぞれの荷重がE点を回す力が0になる式を立てます。
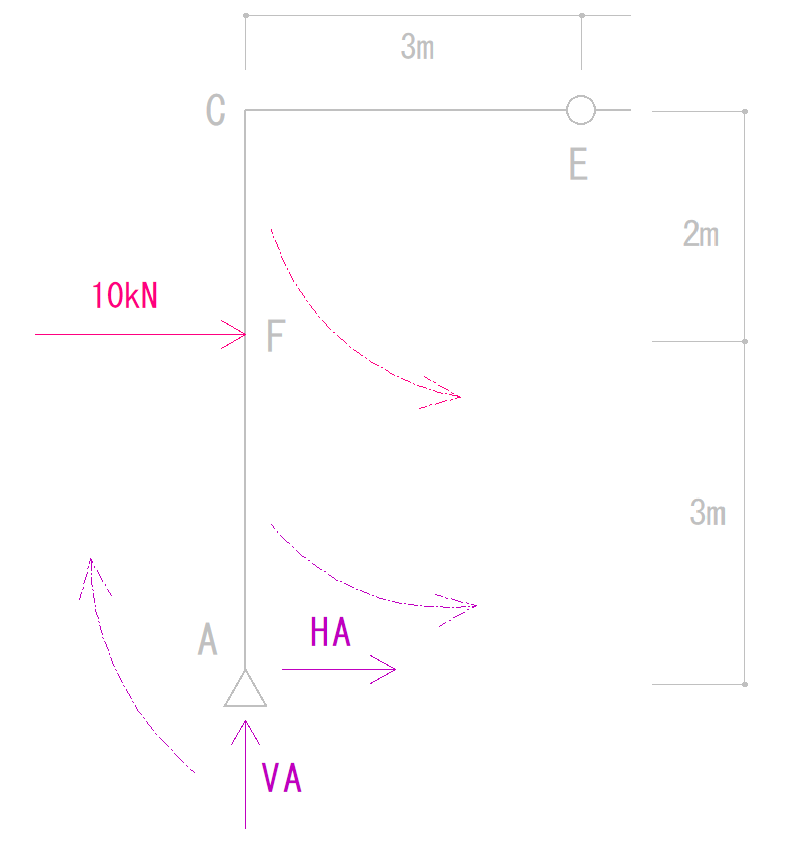
よって、
VA × 3m +(-HA × 5m)+(-10kN × 2m) = 0
※荷重のモーメント力の向きと符号に注意してください。
式を解いていきます。
3VA-5HA-20 = 0 …④
これ以上計算できないので次に進みます。
連立方程式を立てる
これまで出てきた式をまとめましょう。
10kN + HA + HB = 0 …①
VA + VB = 0 …②
VA = -5kN …③
3VA-5HA-20 = 0 …④
③の式でVAの値が分かっているので、そこから芋づる式に次々と計算を進めることができます。
②と③の式より、
-5 + VB = 0
VB = 5kN (仮定通り上向き)
③と④の式より、
3×(-5kN)-5HA-20=0
-35-5HA=0
-5HA=35
HA=-7kN (仮定とは逆向き) …⑤
①と⑤の式より、
10 +(-7kN)+HB=0
HB=-3kN (仮定とは逆向き)
となります。
解答
VA = -5kN (下向き)
VB = 5kN (上向き)
HA=-7kN (左向き)
HB=-3kN (左向き)
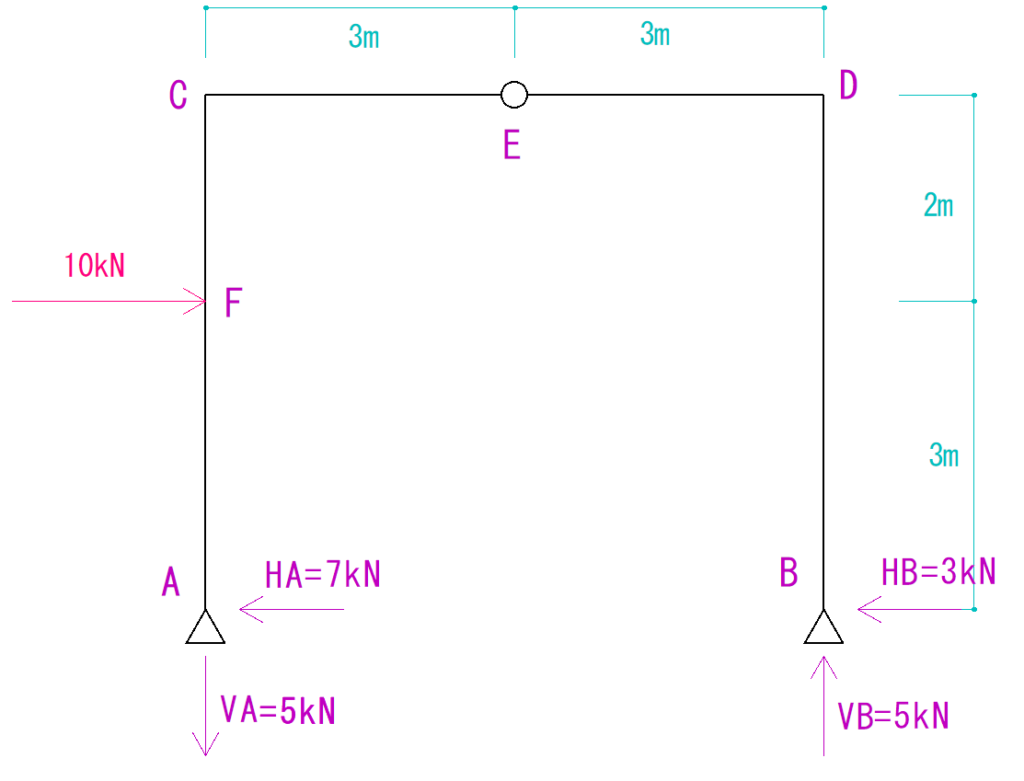
となります。
仮定とは向きが違う場合があるので少し注意しましょう。