今回は単純梁に等変分布荷重がかかった場合のQ(せん断力)図M(曲げモーメント)図の描き方を解説していきたいと思います。
教科書などでは謎の公式が出てきて、詳しい解説などがないのでよくわからない分野だと思います。
公式を覚えたほうが楽だ、という方はそれでいいと思いますが、頭がごちゃごちゃする!という方は、ぜひこの記事で内容を理解しましょう!
この解説をするにあたって、等変分布荷重というのが何かわからないと先に進めません。
復習しておきたい方は下のリンクから見ることができます。
例題
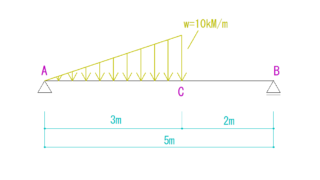
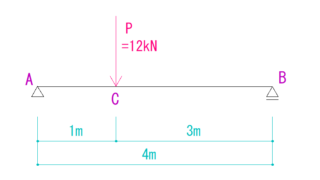
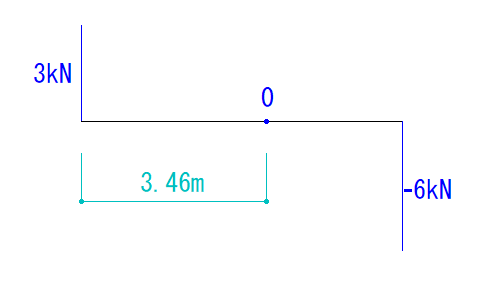
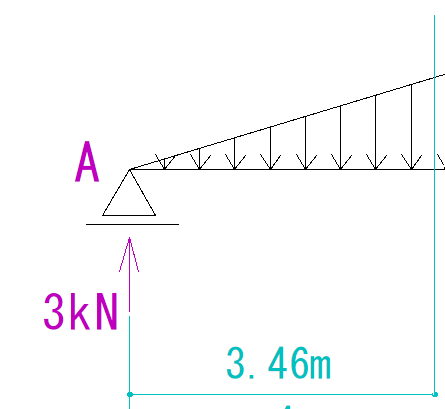
下の図を見てQ図M図を求めなさい。
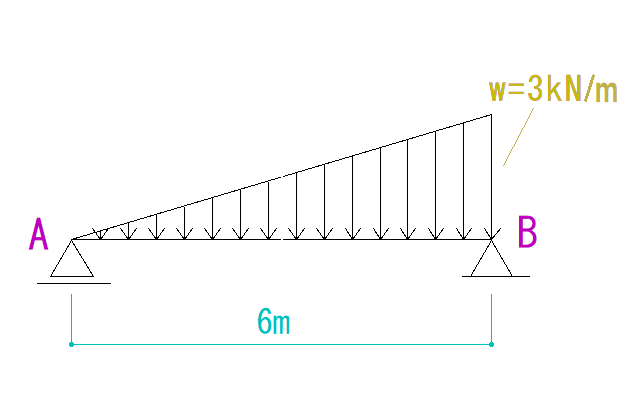
解説
反力の仮定
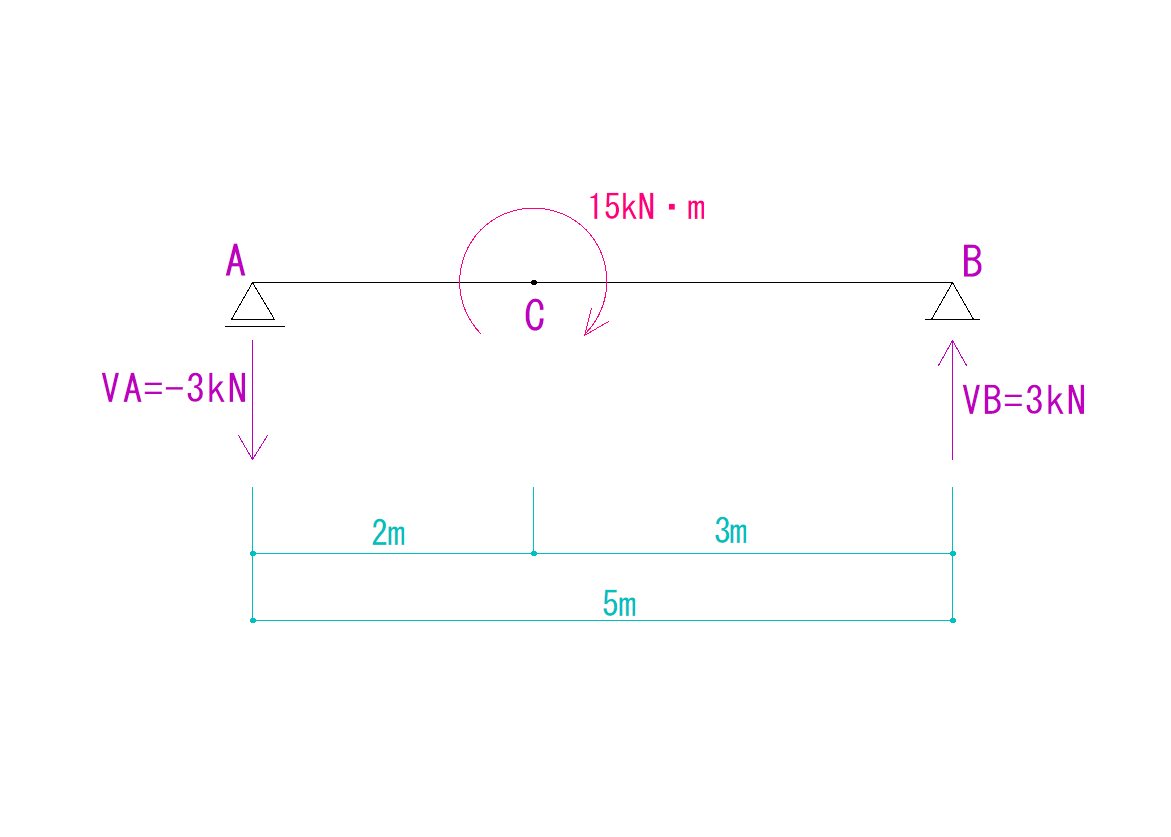
まずは反力を仮定し、求めていきます。
反力の求め方について詳しくは、下のリンクの記事をご覧ください。
今回も、もう一度解説していきたいと思います。
この問題では水平力が働いていないため、水平反力及びN図は省略します。
それでは反力を求めていきます。
まず、このままだと計算がしづらいので等変分布荷重の合力を求めます。
等変分布荷重の合力の大きさは、
等変分布荷重がかかっているところの距離[l]×等変分布荷重の最大厚さ[w]÷2
でした。
このように合力は面積を求めるイメージで求めましょう。
なので今回は
6×3÷2
=9kN
となります。
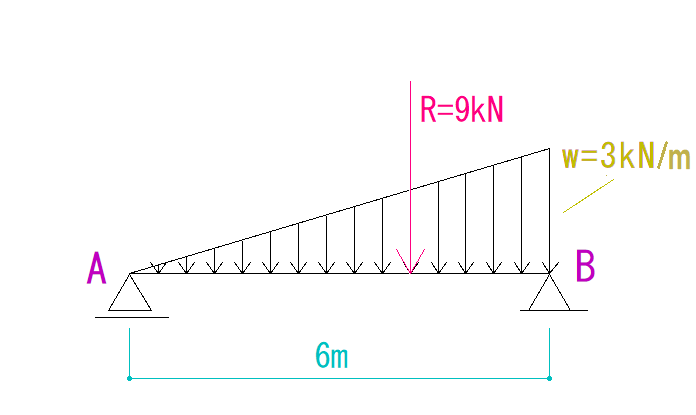
合力のかかる位置は分布荷重の重心です。
直角三角形の重心は、底辺を下にした時の2:1に分けたところにあります。
今後も出てくるので、しっかりと覚えておきましょう。
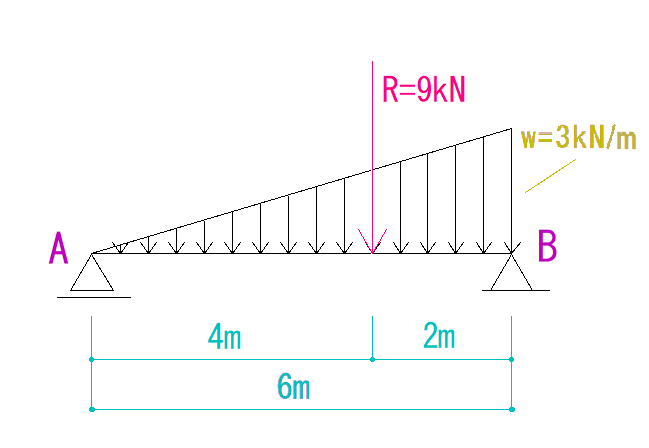
ここまでくると見慣れた形になりました。
あとは力の釣合い条件を使って反力を求めていきます。
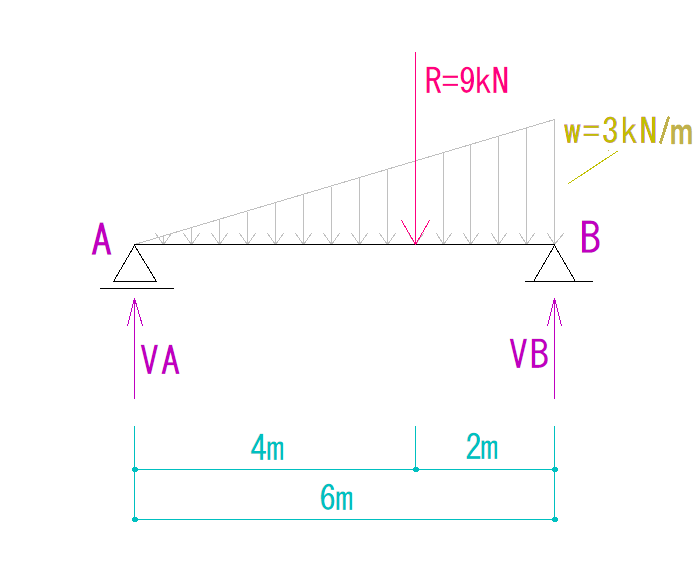
力の釣合い条件については下のリンクを参照
単純梁に集中荷重がかかった場合の反力の求め方については下の記事を参照
A点をO点としてΣMAを考えると、
(-VA×6)+(9×2)=0 …※
-6VA=-18
VA=3kN(仮定通り上向き)
となります。
※(なぜVBにマイナスが付いているかというと、仮定の向きではA点を反時計回りに回すためです。)
ΣY=0より
VB+(-3)+9=0
VB=6kN(仮定通り上向き)
となります。
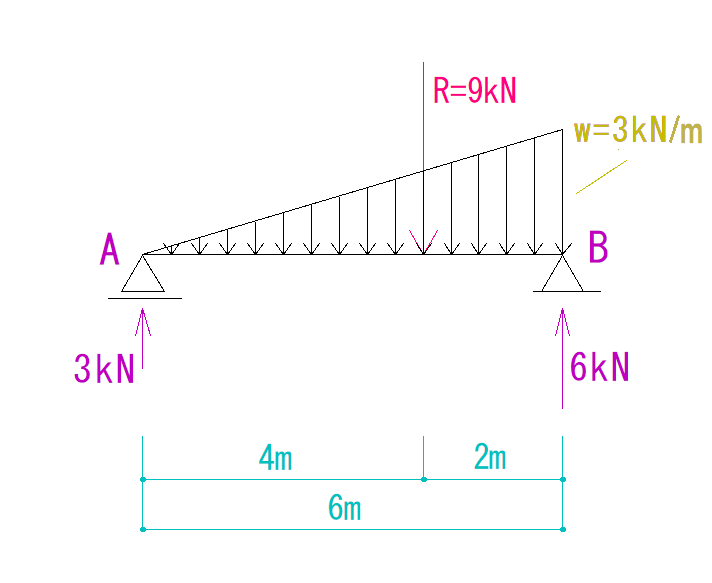
Q図の描き方
それではQ図から書いていきましょう。
やり方は覚えているでしょうか?
問題を左(もしくは右)から順番に見ていきます。
詳しいやり方は下の記事を参照
では左から順にみていきたいと思います。
A点に注目してみましょう。
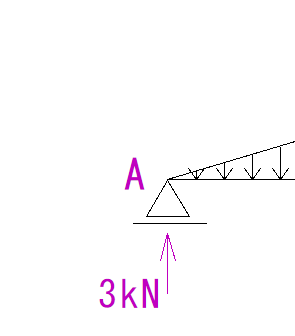
部材の左側が上向きの力でせん断されています。
この場合符号は+と-どちらでしょうか?
下の表で確認しましょう。
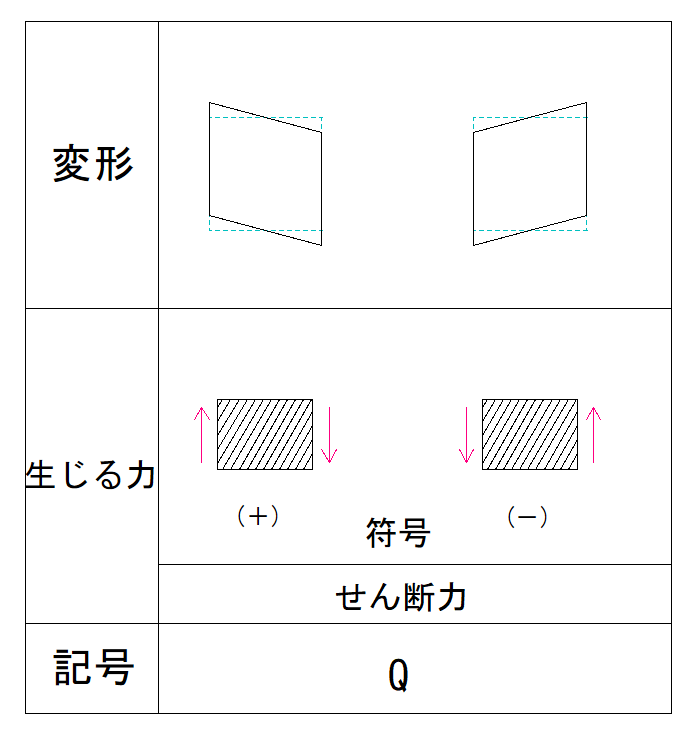
部材の左側が上向きの場合、符号は+となります。
大きさはVAのまま3kNとなります。

…さて、ここからどうしたら良いでしょうか?
初見ではどうしたらいいか想像もつかないと思います。
なので、ここはやり方を丸暗記しましょう!
3ステップです。
1.Q図でVBを求める。
2.せん断力が0になる地点を求める。
3.2次曲線で3点を繋ぐ。
一つずつ考えていきましょう。
1.Q図でVBを求める。
これは簡単です。
先程のVAと同様にやっていきましょう。
部材の右側が上向きの力でせん断されています。
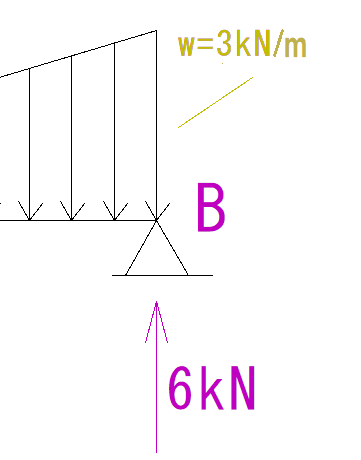
この場合符号は+と-どちらでしょうか?
下の表で確認しましょう。

部材の右側が上向きの場合、符号は-となります。
大きさはVBのまま6kNとなります。

2. せん断力が0になる地点を求める。
ここが一番難関です。
どのように求めればよいでしょうか?
かみ砕いて簡単に解説したいと思います。
まず、問題の図の左半分だけを見ます。
(三角形の先っぽの方半分を見ます)
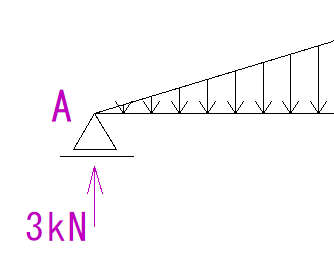
せん断力が0ということは、このVAと等変分布荷重の三角形の大きさが等しいということです。
(上からかかる力と、下からかかる力が等しくなった時(釣合ったとき)せん断力は0になります。)

…ということは、等変分布荷重の三角形の面積が3になる地点を見つけないといけません。
ここから少し難しい話(数学の話)をします。
この等変分布荷重の三角形の面積は底辺のxの距離が分かると自然と分かります。
なぜなら、この三角形の高さと底辺は比例の関係にあるからです。
今回の場合、(底辺)6mで(高さ)0から3kN/mへの変化をしています。
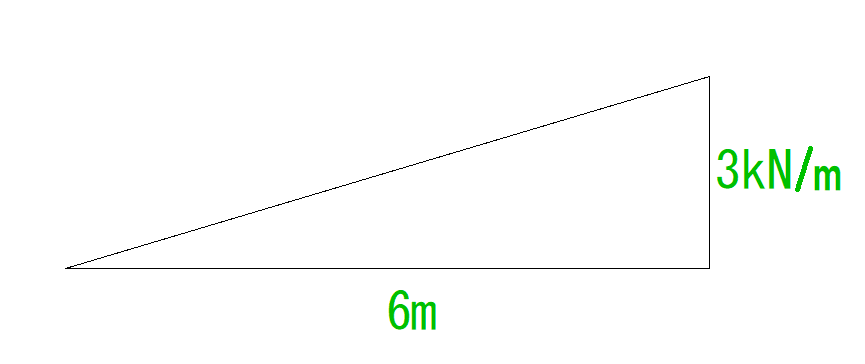
つまり、(底辺)3mの時(高さは)1.5kN/m
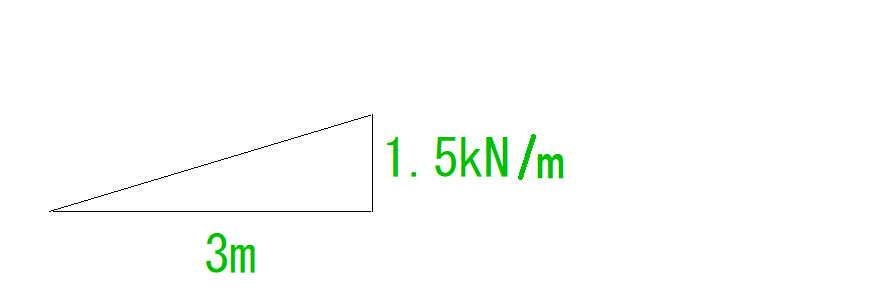
(底辺)2mの時(高さ)1kN/m

(底辺)1mの時(高さ)0.5kN/m
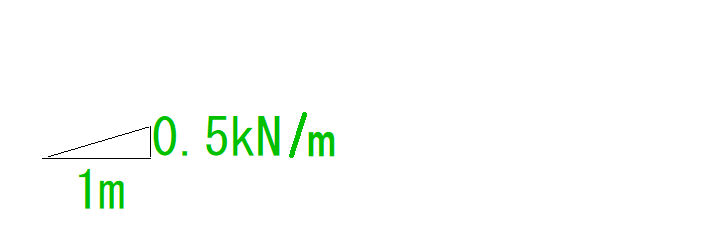
となります。
この時底辺をxとすると、
(底辺)x mの時(高さ)0.5x kN/mとなります。
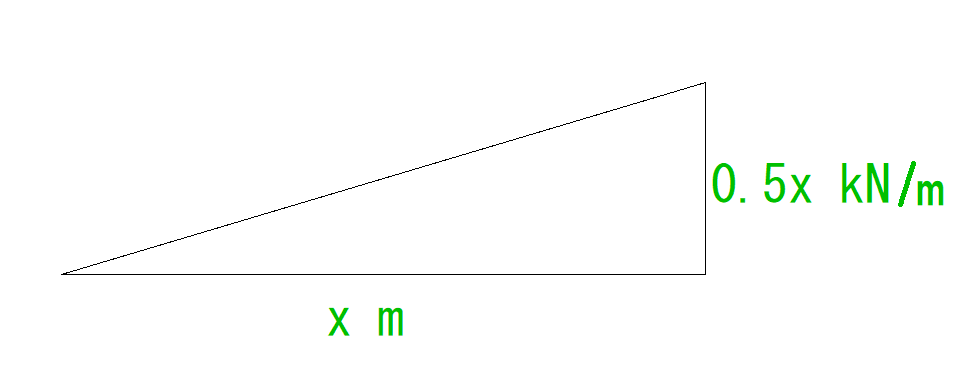
さて、ここまでくると三角形の面積を、xを使って表すことができます。
三角形の面積の公式
(底辺)×(高さ)÷2 より
x × 0.5x ÷ 2
これがこの問題の等変分布荷重の三角形の大きさです。
ここまで来てようやく、本題に戻れそうです。
この三角形がどの地点で面積が3になるか、ということでした。
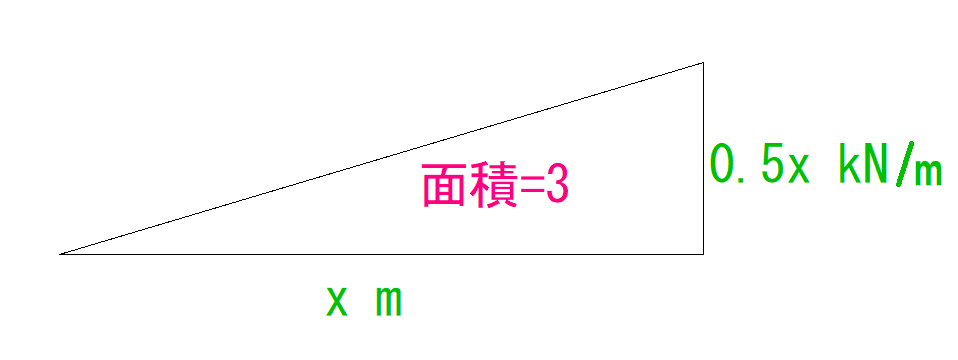
なので公式に当てはめます。
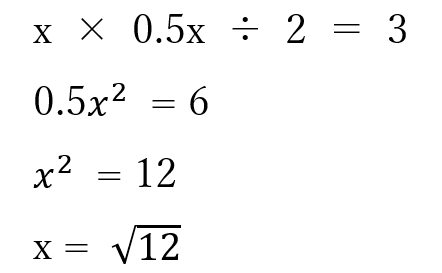
ここまで来たら関数電卓で少数第二位ぐらいまでを求めます。
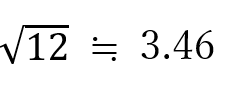
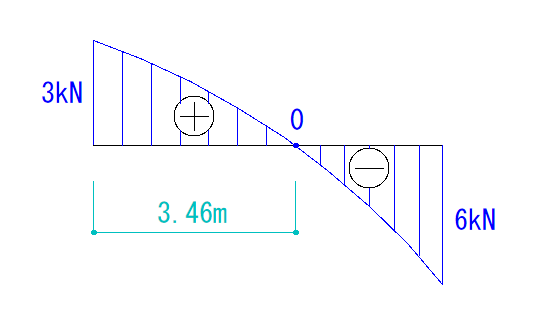
Q図で0になるのはVAから右に3.46mの地点となります。
ここはかなり難しい分野です。
是非じっくりと覚えてください。
3. 2次曲線で3点を繋ぐ。
なぜ、2次曲線なのか、というのは先回の記事
を見ていただくとわかると思いますが、結局のところ、式に2乗が出てくるからなんです。
先程やったときxを2乗しましたよね。
だからです。
(詳しくは先回の記事を見てください)
ただ、2次曲線なんてきれいにフリーハンドできれいに描けません。
なので、VA点、0点、VB点の3点を曲線で繋げば正解になります。
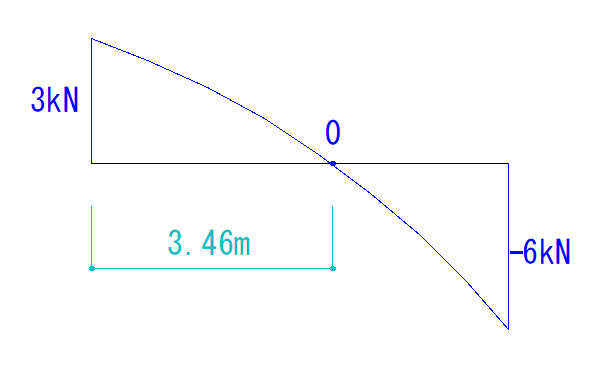
最後に符号と大きさ、そして忘れず0点の距離を書き込みましょう。
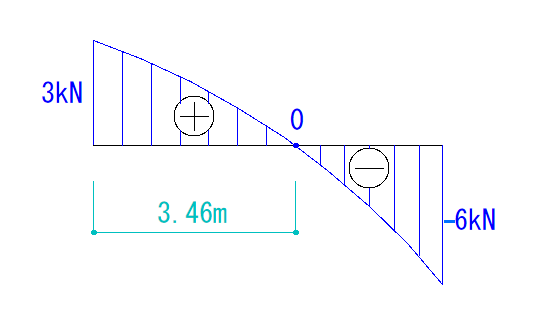
M図の描き方
さて、M図ですが、まずは形を覚えましょう。
等変分布荷重のM図は3次曲線になります。
…3次曲線…わからない…と落ち込まないでください!
この分野で回答するときは、形はあまり重要視されません!
気持ち細長い2次曲線を描いて、Mmaxを求めれば正解をもらえます。
符号の求め方
まず符号を確認しましょう。
下の表で確かめます。

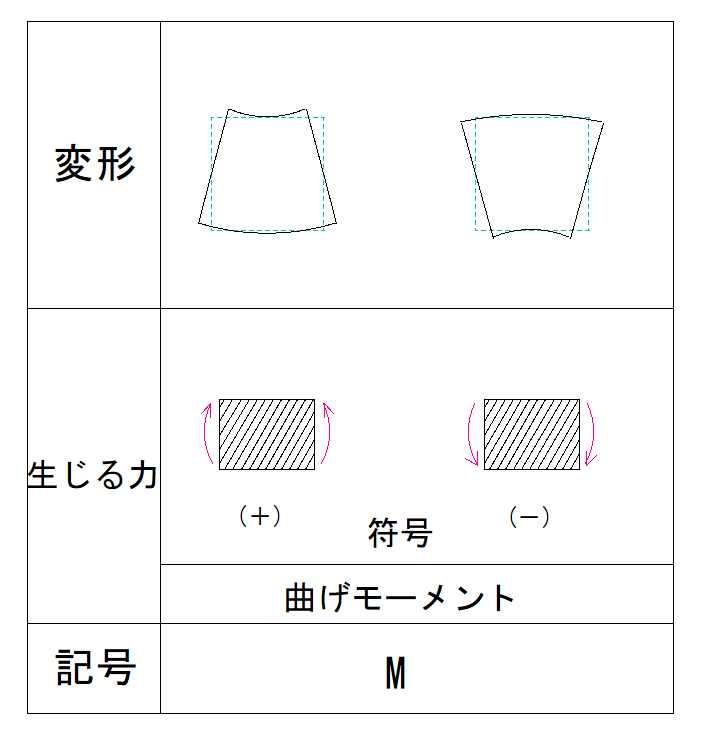
今回はプラスのようなので、下に出る形になることが分かります。
Mmaxの求め方
では、Mmaxはどの地点でしょうか?
先回も言いましたが
Q値が0の時がM値最大
です。
しっかり覚えましょう。
Q値が0の地点は先程求めています。
VAから右に3.46mの地点でした。
なので、その地点から左側の図だけを見ます。
(右側を見ても答えは出ますが、式がめんどくさいので三角形の先っぽの方を見るのをお勧めします。)
あとは等変分布荷重の合力とモーメント力、VBのモーメント力をそれぞれ求めて足してあげればMmaxは出ます。
式がごちゃごちゃして、筆記で解くのは大変だと思うので、ぜひ関数電卓を有効活用しましょう。
細かい解答方法は今回や以前の記事と内容が被るので割愛します。
詳しくは下のリンクの記事をご覧ください。
等変分布荷重の合力の大きさと合力のかかる位置は以下の通りです。

そうしたら式を作ります。

※最初のマイナスを忘れずに…
あとは関数電卓に任せると、
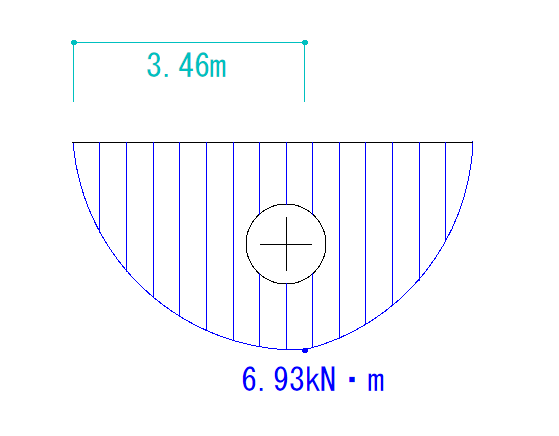
=6.93kN・m
となります。
あとは任意の位置に点を取り、3次曲線でM図を書きます。

Mmaxと符号を書き込んで終了です。