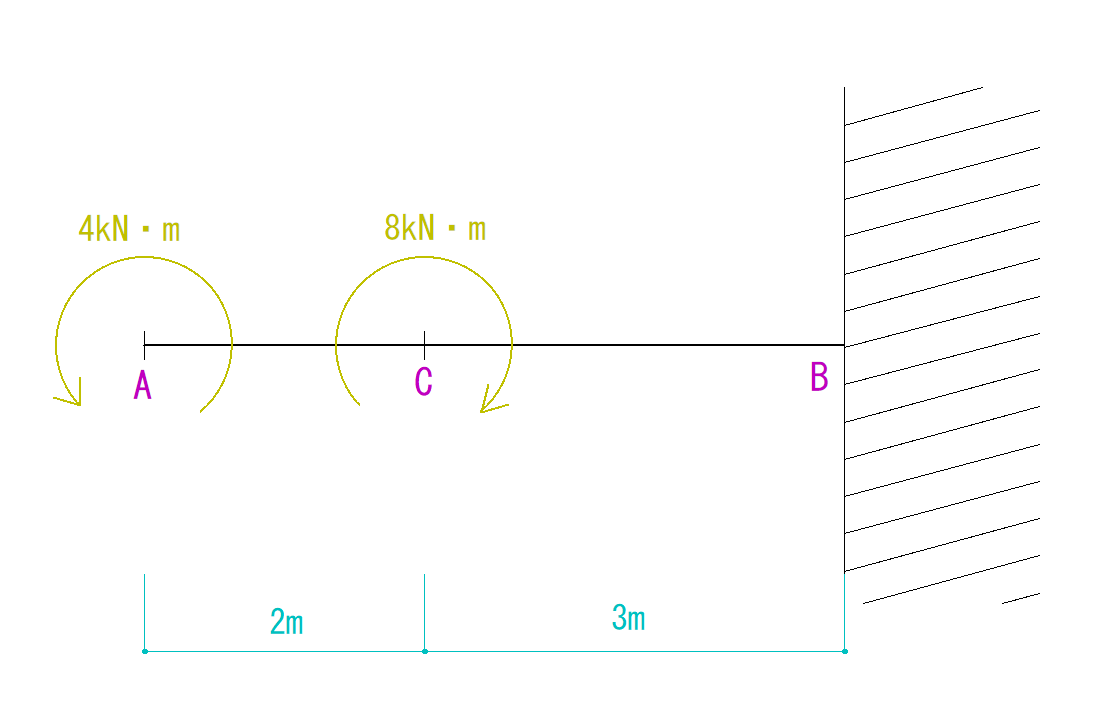
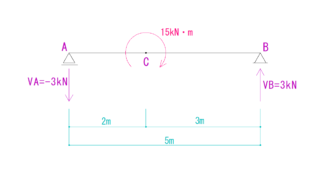
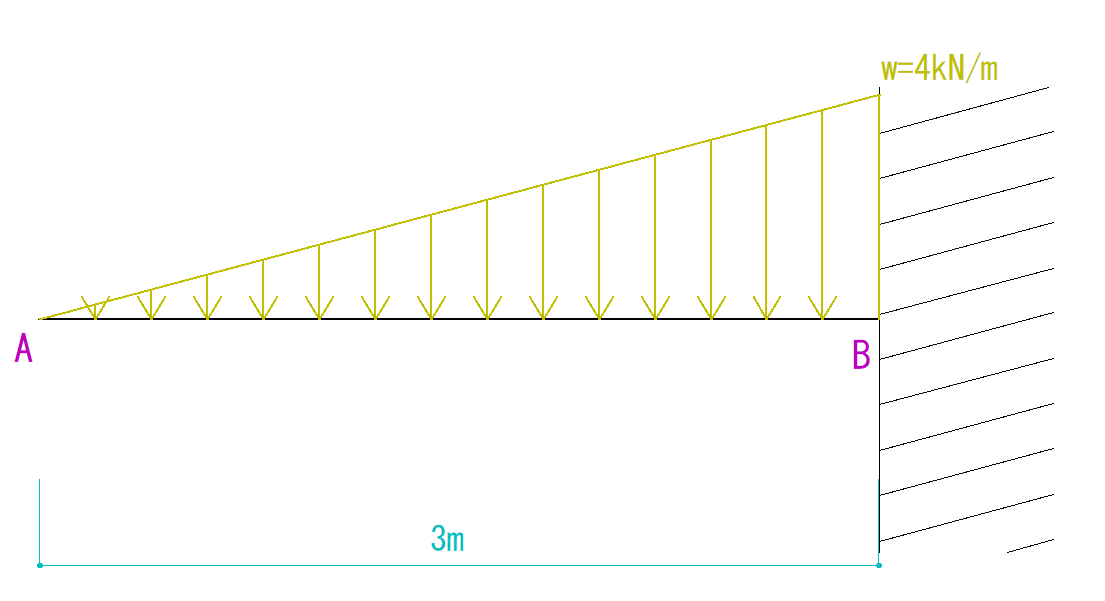
今回は片持梁にモーメント荷重がかかった場合のQ(せん断力)図M(曲げモーメント)図の描き方を解説していきたいと思います。
モーメント荷重と聞くと、少しややこしそうな感じがしますが、実はとてもラッキーな分野です。
しっかりと理解して、自分の得意分野にしていきましょう。
例題
下の梁を見てM図を求めなさい。
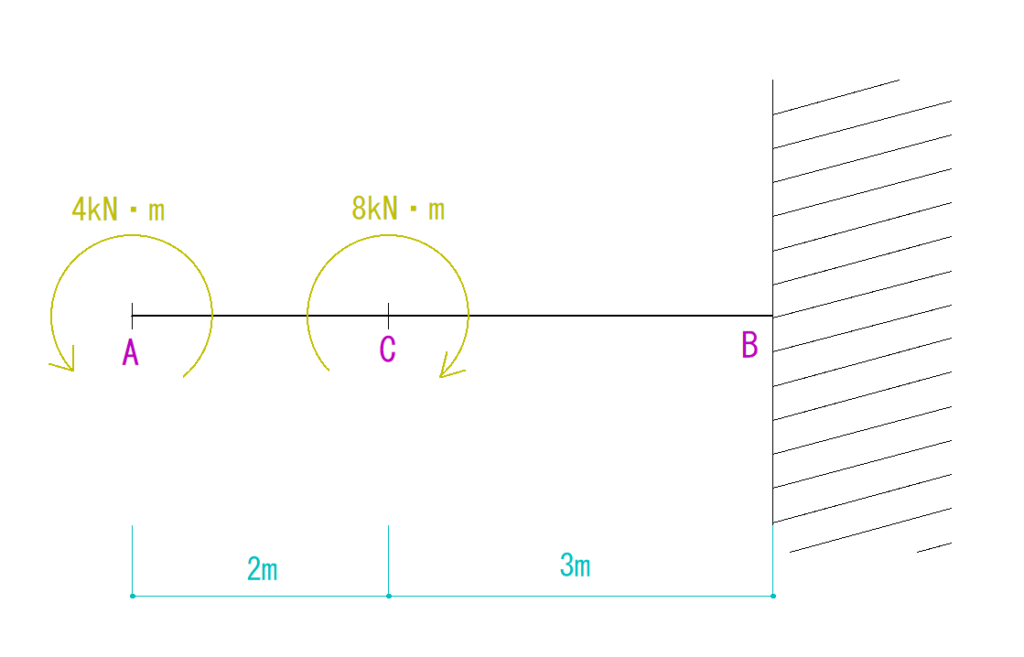
解説
まず、注目するべきなのは問題文です。
「下の梁を見てM図を求めなさい。」
つまり今回はQ図も書く必要がありません。
なぜでしょうか?
Q図を描く必要がない理由
Q図を描く必要がない、つまり垂直方向の反力(VB)は0になるということです。
なぜそうなるのでしょうか?
まず、モーメント荷重には垂直力も水平力もありません。
ただ回すだけの力です。
しかし、単純梁の場合は、なにも反力を指定しないと回ってしまうのでVA,VBの「偶力」を用いて回転を止める必要がありました。
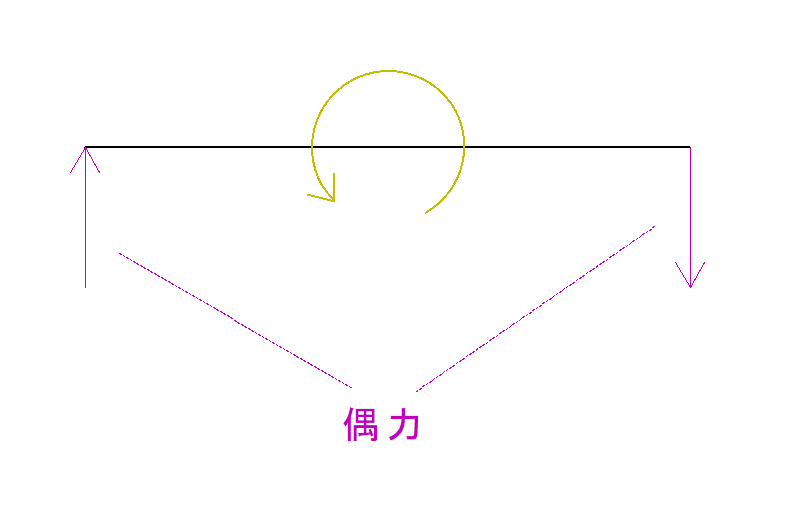
下のリンクからその時の記事を読むことができます。
ではなぜ、今回はその垂直方向の反力もいらないのでしょうか?
答えは、モーメント反力があるから、です。
モーメント荷重がかかった場合はモーメント反力が直接打ち消すので、ほかの荷重は必要ないのです。
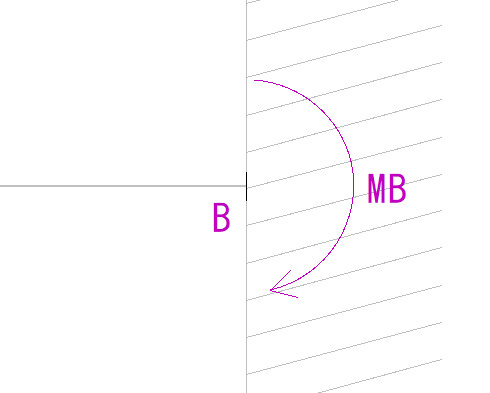
M図の描き方
MBの決定
まずMBの大きさを求めます。
MBの向きは下の図のようにプラスに仮定します。
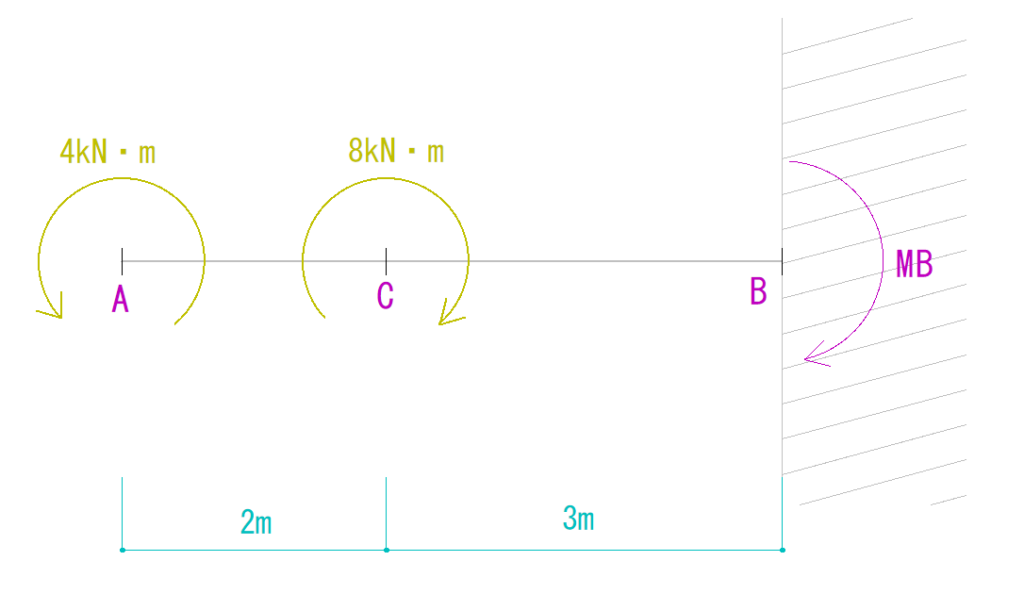
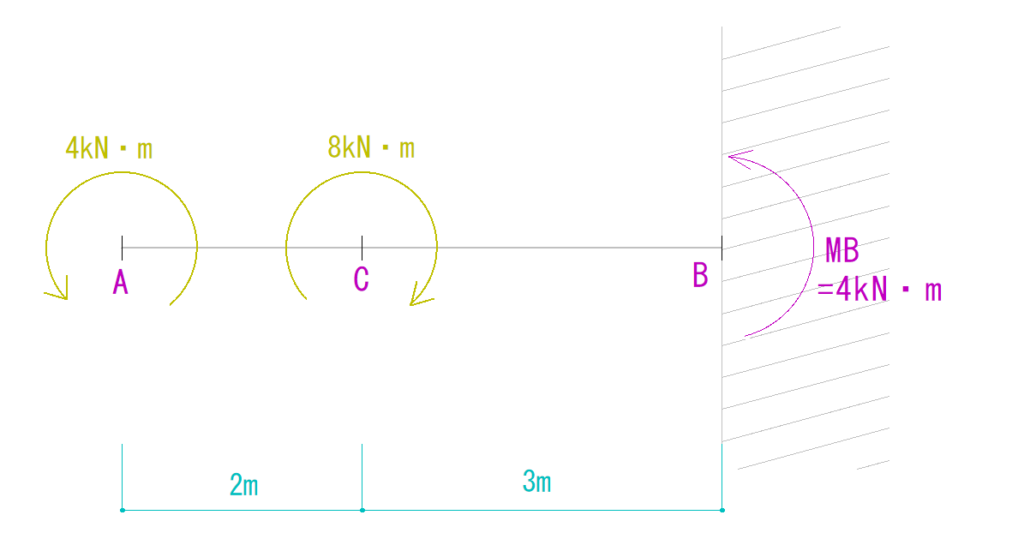
ΣMB=0より、
-4kN・m + 8kN・m + MB = 0
MB = -4kN・m(仮定とは逆の反時計回り)
となります。
M図
では早速M図を描いていきましょう。
今回は二つのモーメント荷重がかかっています。
左から(右からでも可)順番に見ていきましょう。
最初はA点です。
大事な点ですが、モーメント荷重のかかった梁を左から順番に見ると決めた場合、モーメント荷重自体も左半分を見ないといけません。
(端と端だけを求める場合など、あてはまらない場合もあります。)
そうしないと、符号がごちゃごちゃになってしまいます。
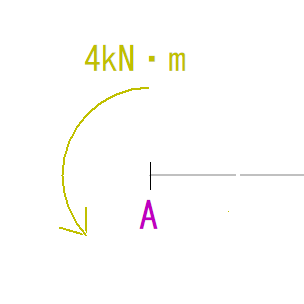
ということで、A点にかかるモーメント荷重の向きを見ると、符号がマイナスということが分かります。
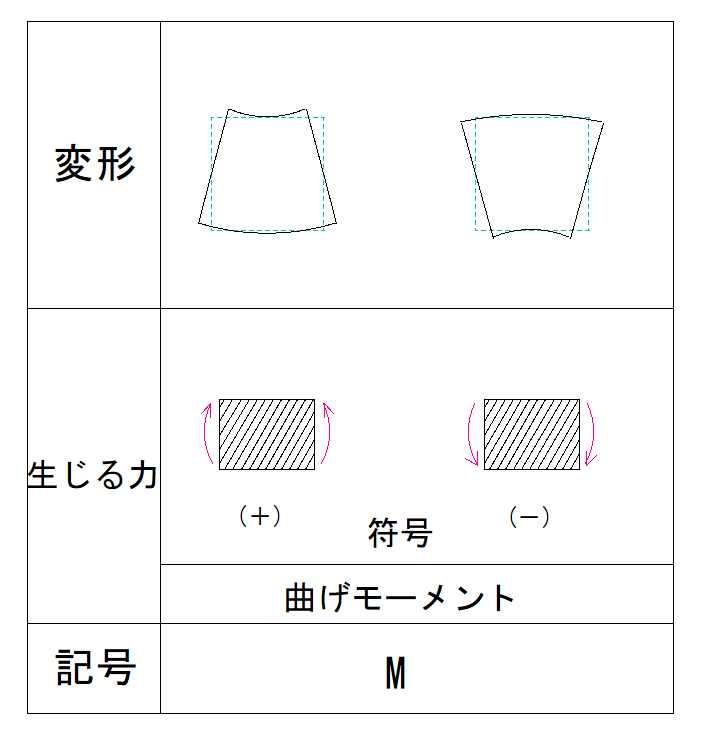
大きさはそのまま4kN・mです。

次にC点に目を移します。
ここも左半分を見ましょう。
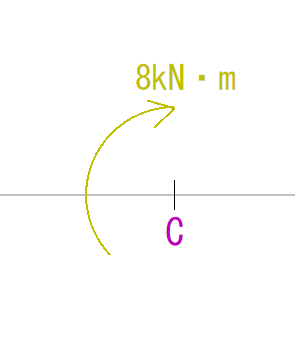
そうすると、符号はプラスになることが分かります。
大きさはそのまま8kN・mです。
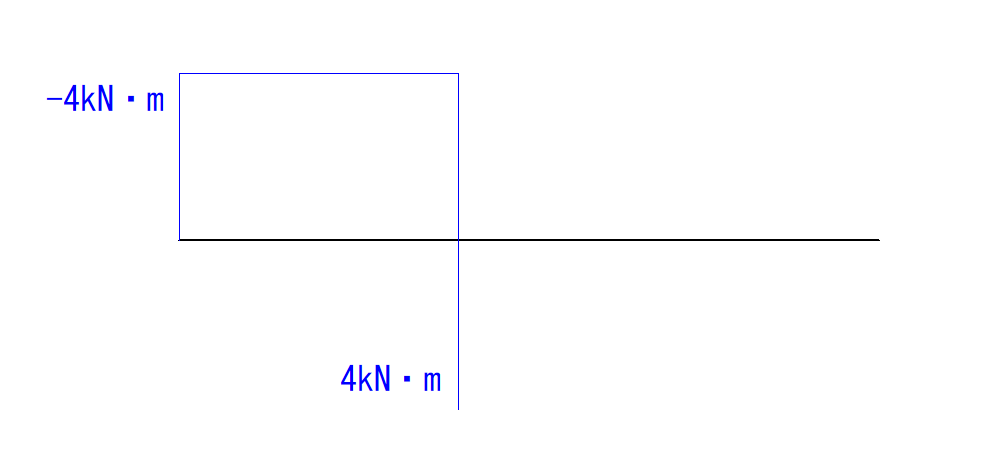
M図は-4kN・mできているので、足してあげます。
-4kN・m + 8kN・m = 4kN・m
M図に書き入れてあげましょう。
最後はB点です。
ここまでくれば最後は0に落としてあげるだけですが、確認のためにMBも考えてみます。
MBは左側を見ると符号はマイナスです。
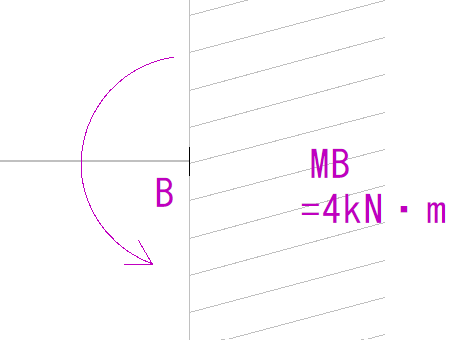
大きさは4kN・mとなります。
M図は4kN・mできているので、足してあげると0になります。
4kN・m + -4kN・m = 0
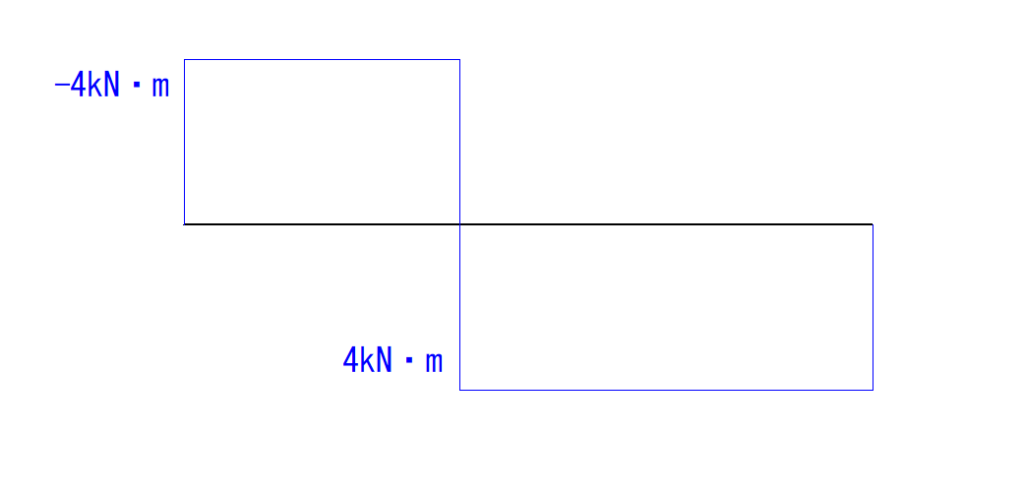
これで完成です。
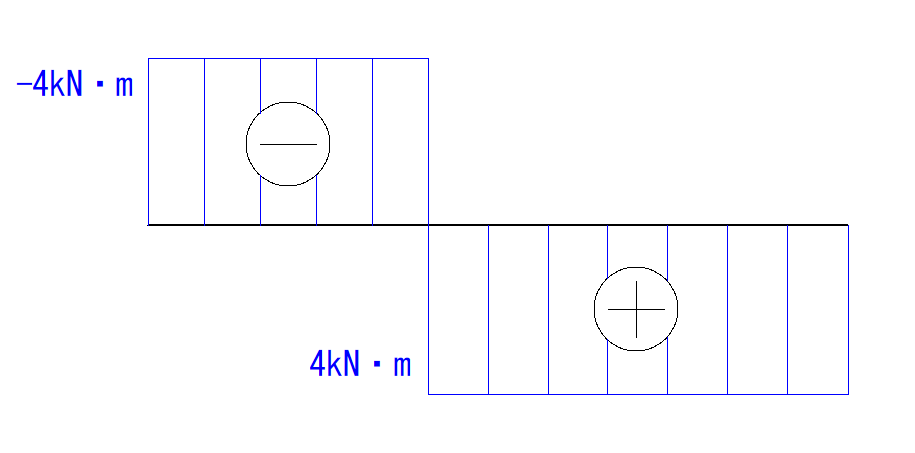
まとめ
焦らず、一つ一つ考えれば難しくない分野です。
しっかりと自分が点を取れる範囲にしましょう!