さて、梁におけるQ図M図の描き方は最後になります。
今回は片持梁に等変分布荷重がかかった場合のQ(せん断力)図M(曲げモーメント)図の描き方について解説していきます。
等変分布荷重については下のリンクの記事から詳しく知ることができます。
例題
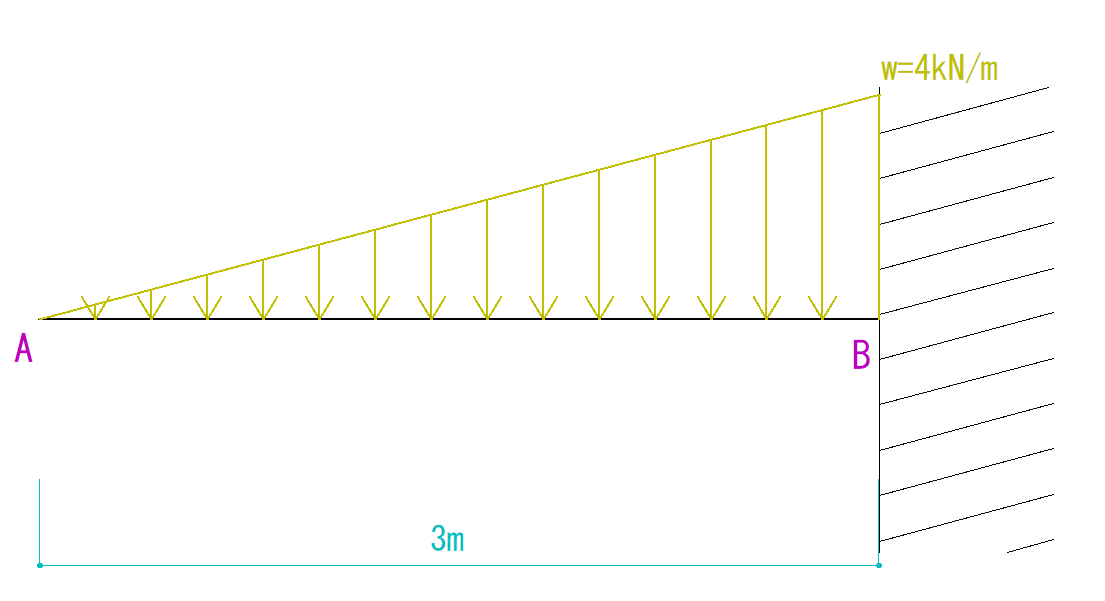
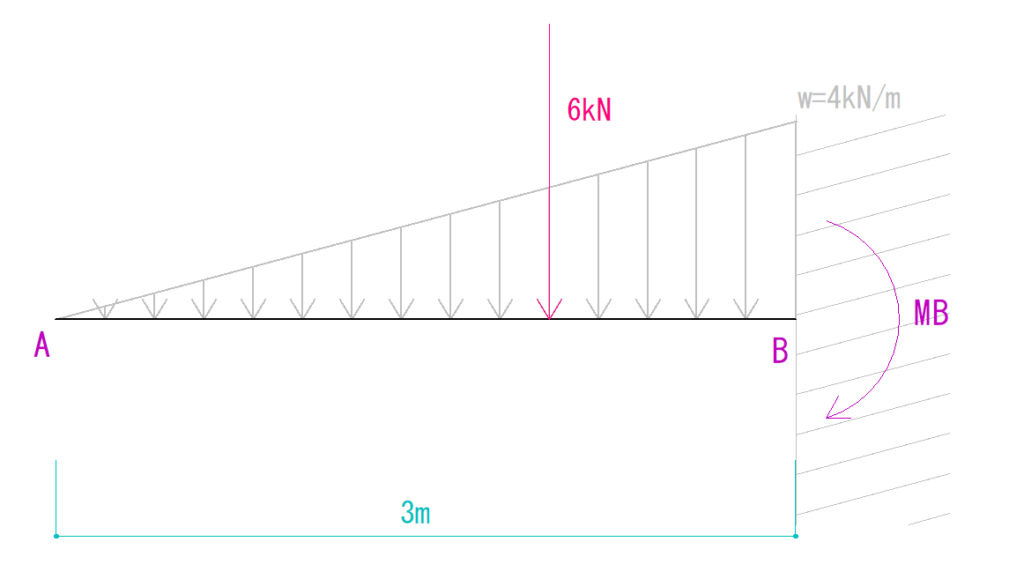
下の図を見てQ図M図を求めなさい。
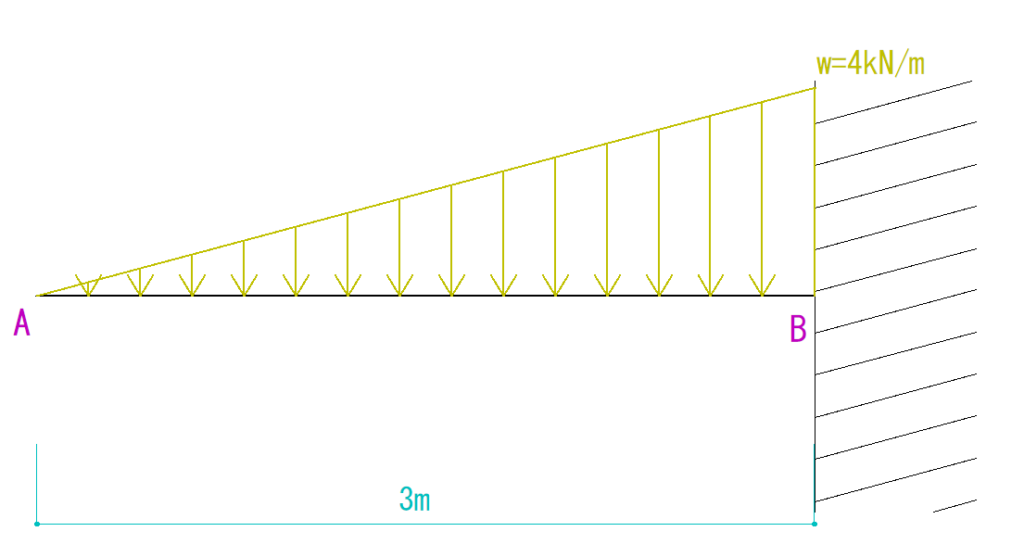
解説
反力の仮定
支点は一つしかないので、荷重に対応する反力をそれぞれ求めていくことで、簡単に求めることができます。
水平反力は0なので求めません。
VBの求め方
VBを上向きに仮定し、等変分布荷重の合力をまず求めます。
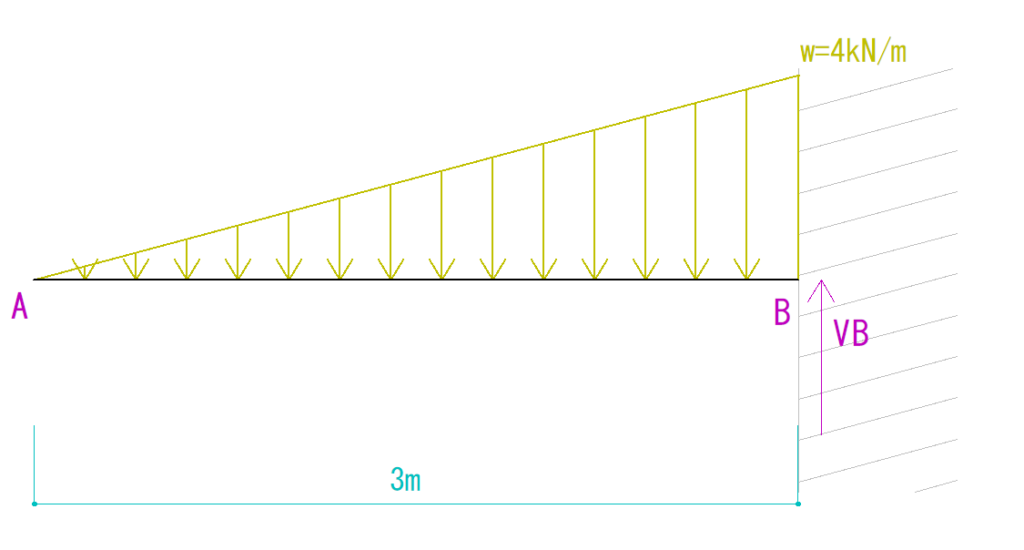
合力の大きさは、等変分布荷重の面積と同じです。
等変分布荷重がかかっているところの距離[l]×等変分布荷重の最大厚さ[w]÷2
の公式から、
3m × 4kN/m ÷ 2 = 6kN
下向きなのでマイナスをつけて-6kNとなります。
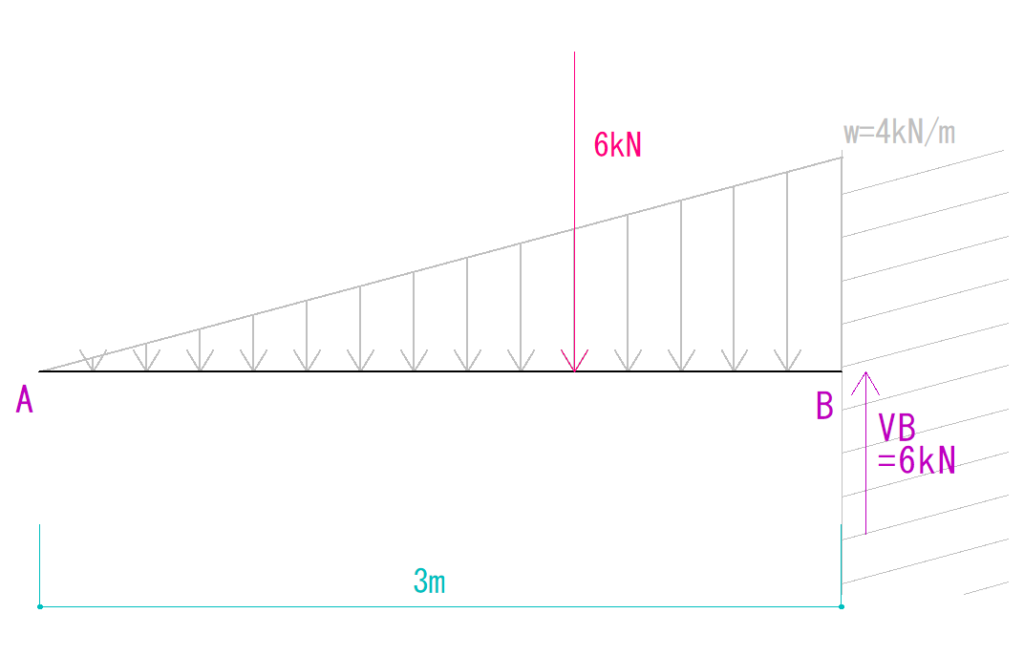
ΣY=0より、
-6kN + VB = 0
VB=6kN(仮定通り上向き)
MBの求め方
等変分布荷重はB点をどれぐらいの大きさで回しているでしょうか?
まずは、MBを時計回りに仮定します。
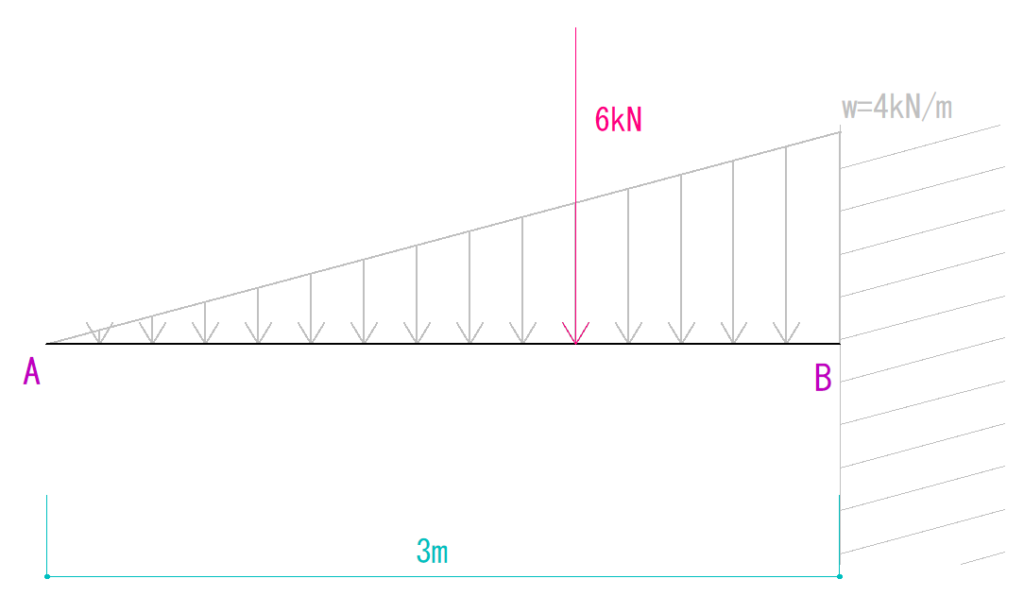
等変分布荷重の合力の大きさは先程計算で出すことができました。
あとは合力のかかる場所を求めます。
合力は等変分布荷重の重心にかかります。

詳しくは下のリンクの記事をご覧ください。
よって、A点から右に2mの場所ということができます。
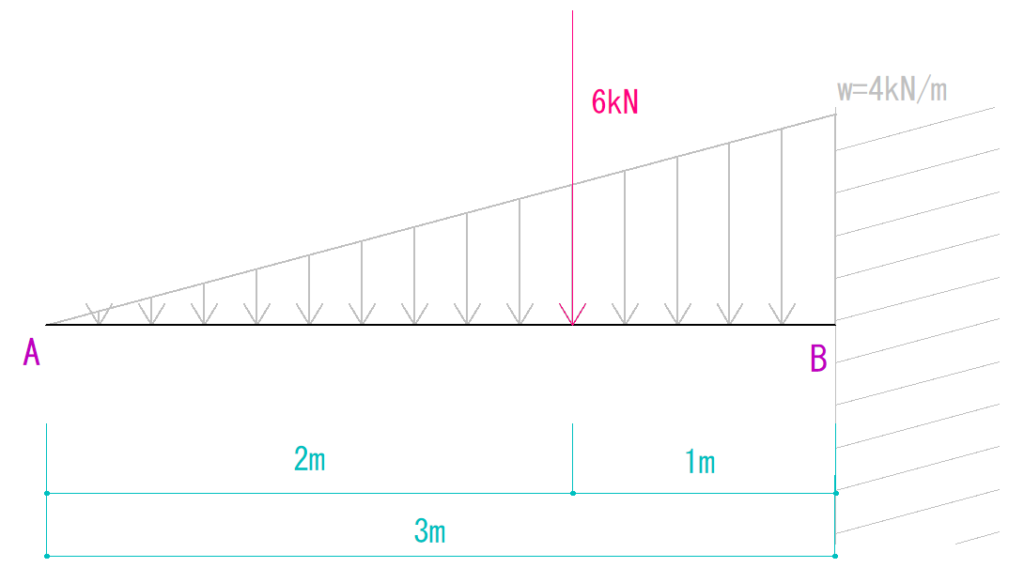
そこから合力がB点を回す力を求めます。
6kN × 1m = 6kN・m
これは反時計回りにB点を回すのでマイナスをつけて
-6kN・mとなります。
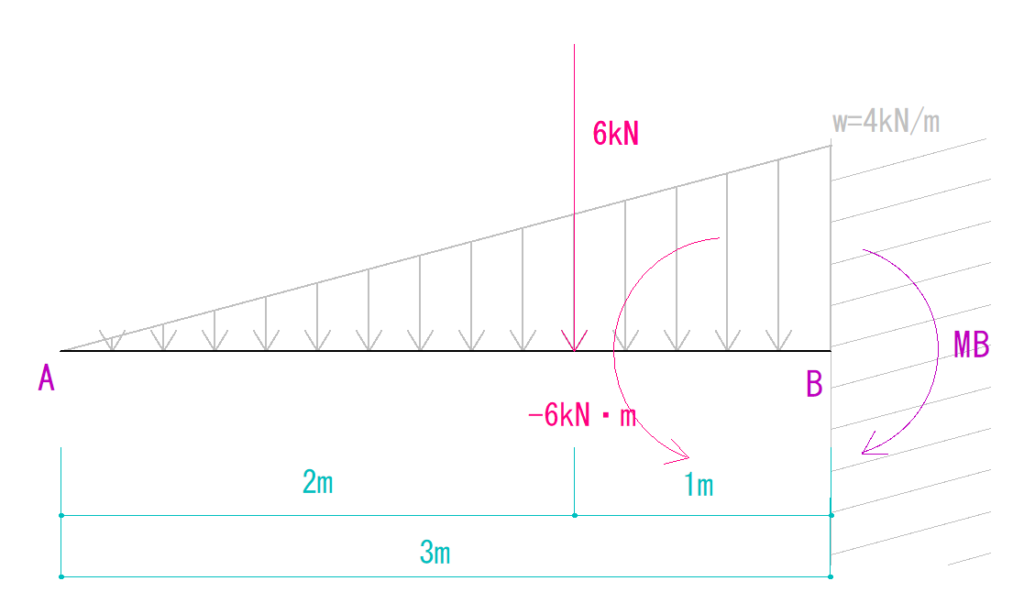
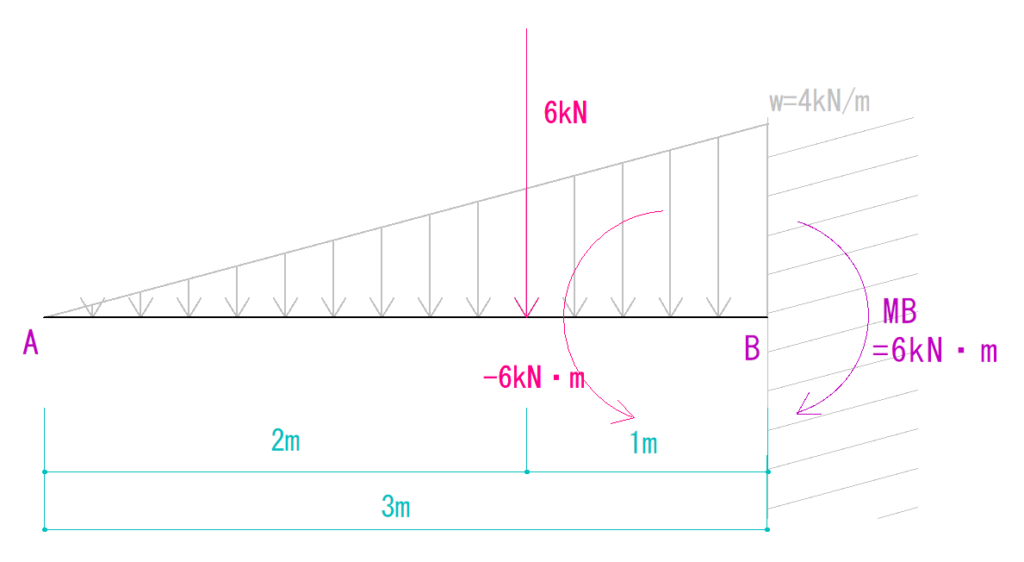
ΣMB=0より
-6kN・m + MB = 0
MB = 6 kN・m(仮定通り時計回り)
となります。
Q図の描き方
等変分布荷重がかかる場合、Q図は2次曲線になります。
つまり、端と端の大きさがわかれば描くことができるということです。
では左から(右からでも可)順にみていきましょう。
A点ですが、支点がありません。
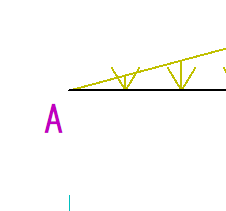
よってQ図の値も0になります。

つぎにB点です。
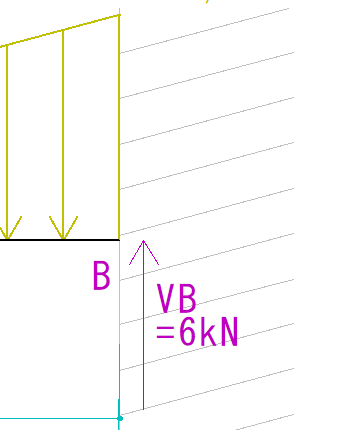
B点のQ図の値はVBの値と等しくなります。
なので大きさは6kNとなります。
符号は下の表で確認してみましょう。
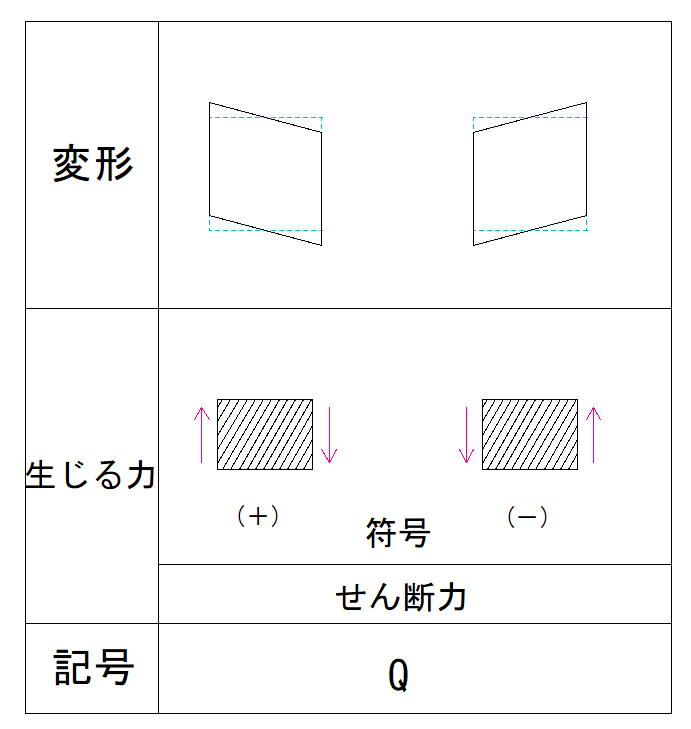
部材の右側を上向きにせん断しているので符号はマイナスだとわかります。
よってB点は-6kNとなります。

あとはA点とB点を2次曲線でつなぎます。
変化量(等変分布荷重の大きさ)は右に行くほど大きくなっているので、2次曲線の変化量も右に行くほど大きくします。
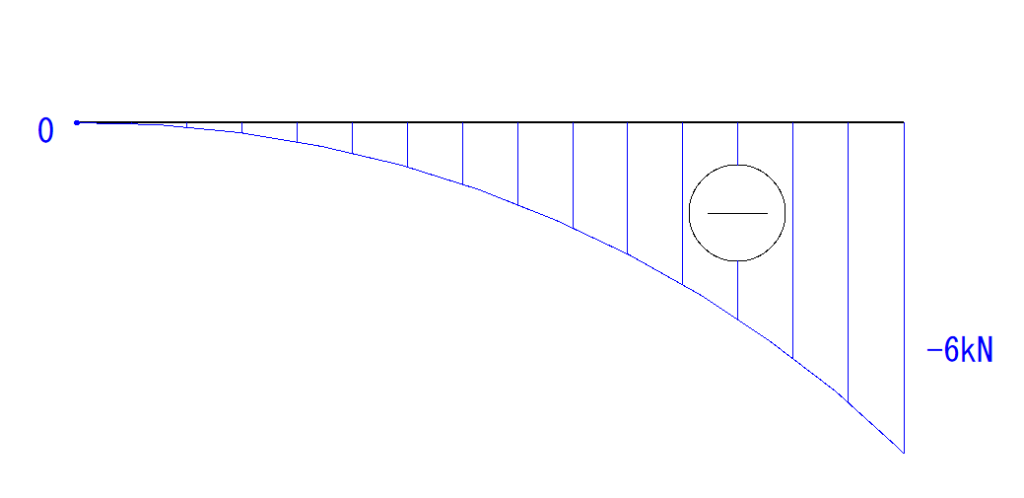
これで完成です。
M図の描き方
等変分布荷重がかかる場合、M図は3次曲線になります。
形はほぼ2次曲線と同じと考えてください。
それではA点から考えてみます。

A点には支点がないのでM値ももちろん0です。

次にB点です。
B点のM値はMBと同じ大きさになります。
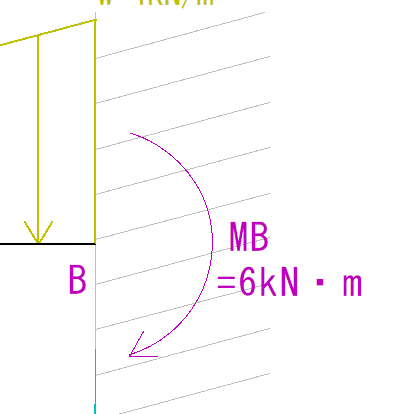
よって大きさは6 kN・mです。
符号ですが、部材の上側を引っ張るような力なのでマイナスだとわかります。
よって-6 kN・mとなります。

あとはA点とB点を3次曲線でつなぎます。
先程と同じように変化量は右に行くほど大きくなっているので、3次曲線の変化量も右に行くほど大きくなっていきます。
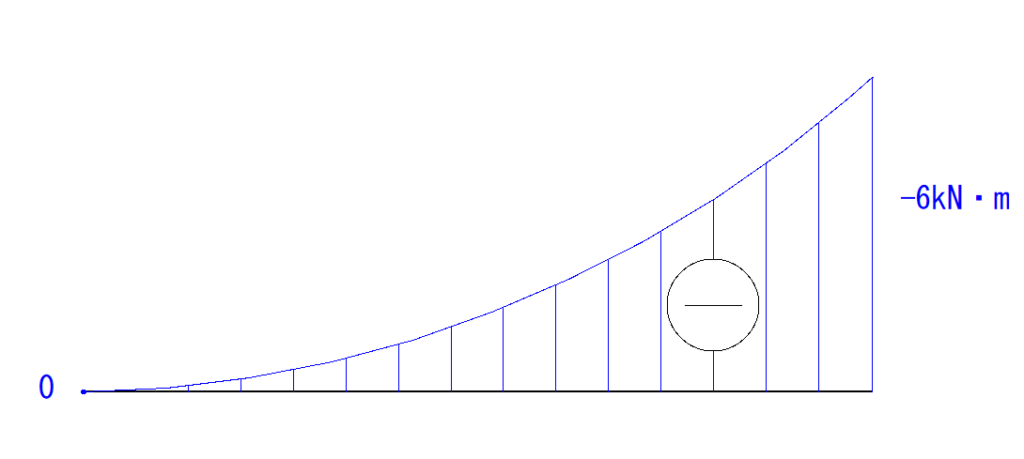
これで完成となります。