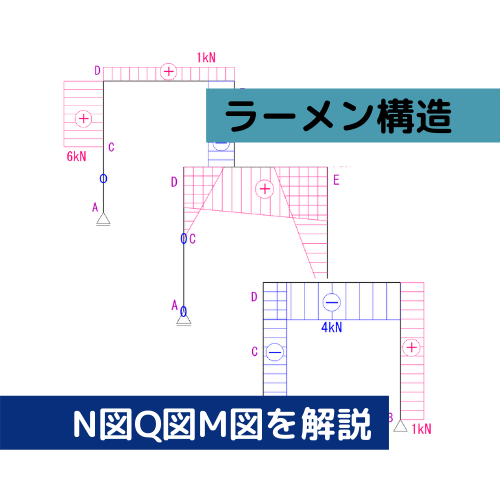
さて今回から、ラーメン構造のN図Q図M図の描き方を解説していきたいと思います。
今回は片持梁系ラーメンです。
この分野を行う前に、まずはN図Q図M図とは何か、片持梁系ラーメンとは何か、また反力の求め方について理解しておかなければなりません。
理解しているか少し不安でしたら下のリンクの記事をご覧ください。
例題
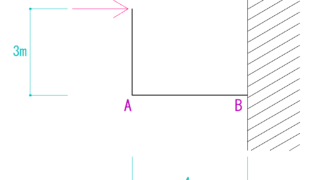
下のラーメン構造のN図Q図M図を描きなさい。
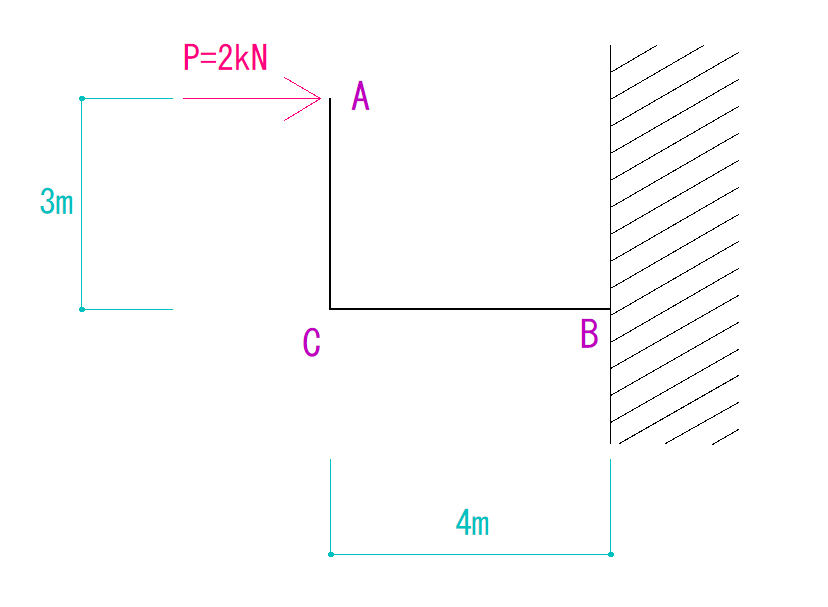
解説
反力を求める
まずは反力を求めなければなりません。
反力の求め方については以前の記事で解説しているのでここでは割愛します。
詳しくは下のリンクの記事で解説しています。そちらをご覧ください。
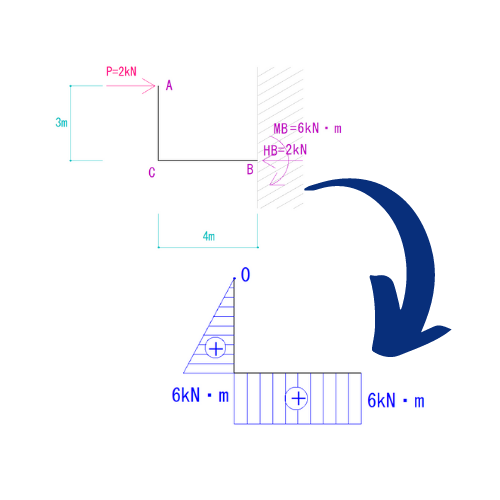
計算すると下の図のようになります。
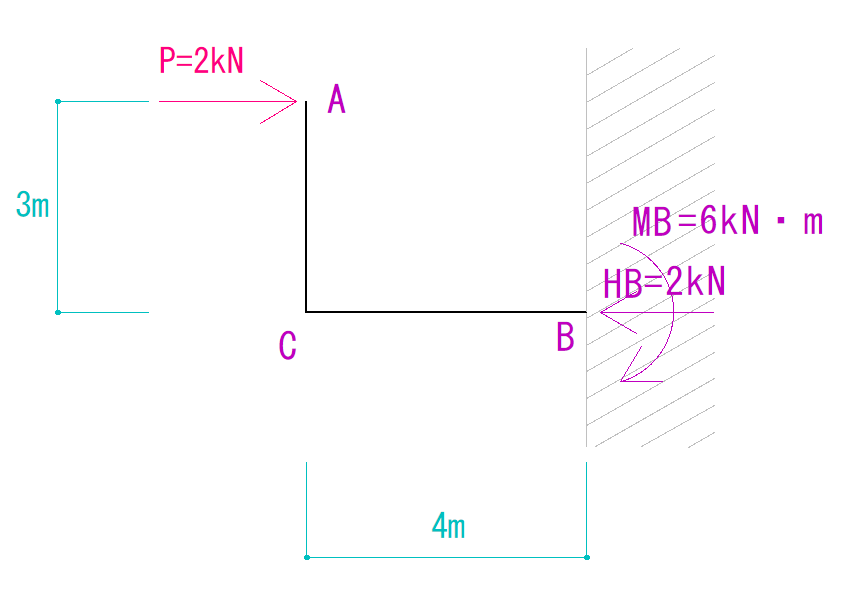
さて、ここから図を描いていきましょう!
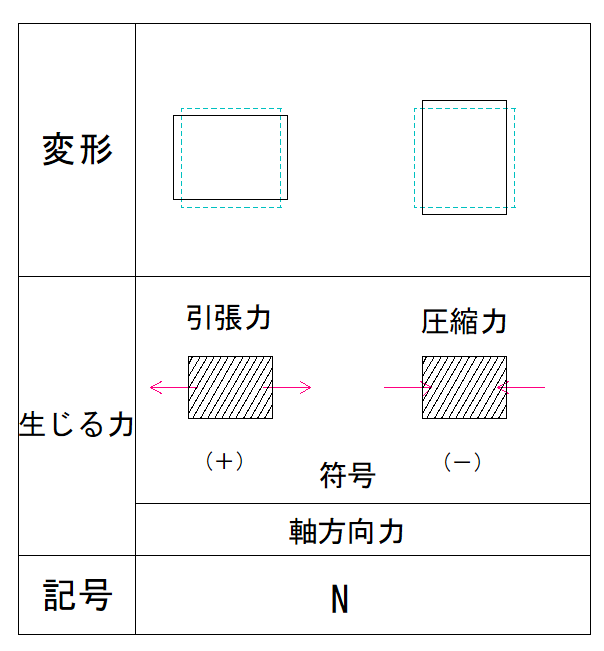
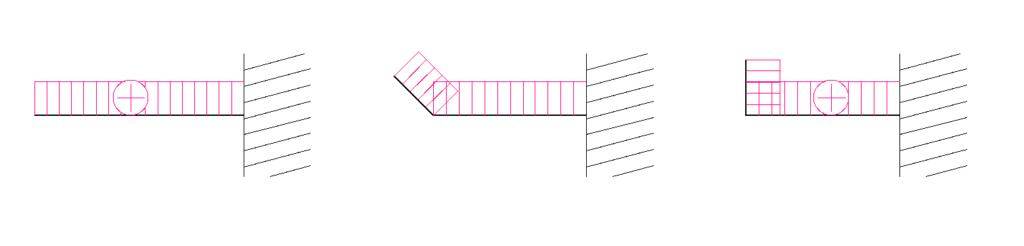
N図の描き方
まず、片持梁系ラーメンは軸方向が途中で変わっていることを理解しないといけません。
AC間は上下が軸方向
CB間は左右が軸方向になっているからです。
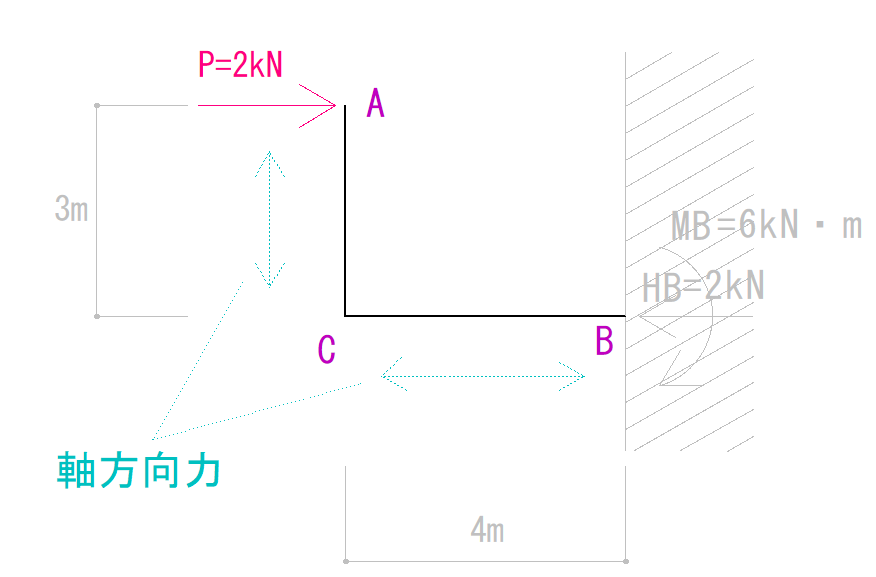
そこでACとCBで分けて考える必要があります。
ACの軸方向力
ACだけを見てみましょう。
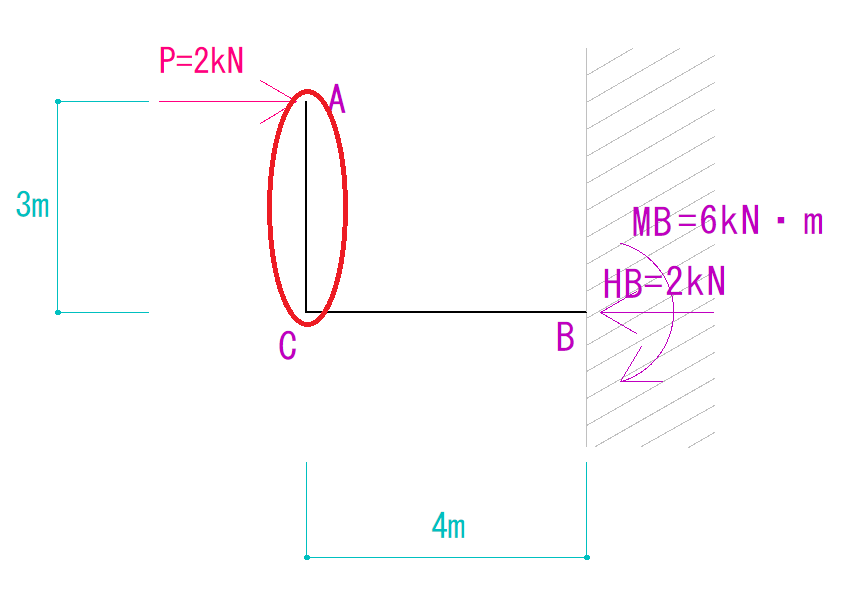
荷重として左から右向きにかかる力はありますが、軸方向にかかっている力(圧縮力や引張り力)はありません。
つまり、ACの軸方向力は0ということが分かります。
CBの軸方向力
次にCBだけを見てみます。
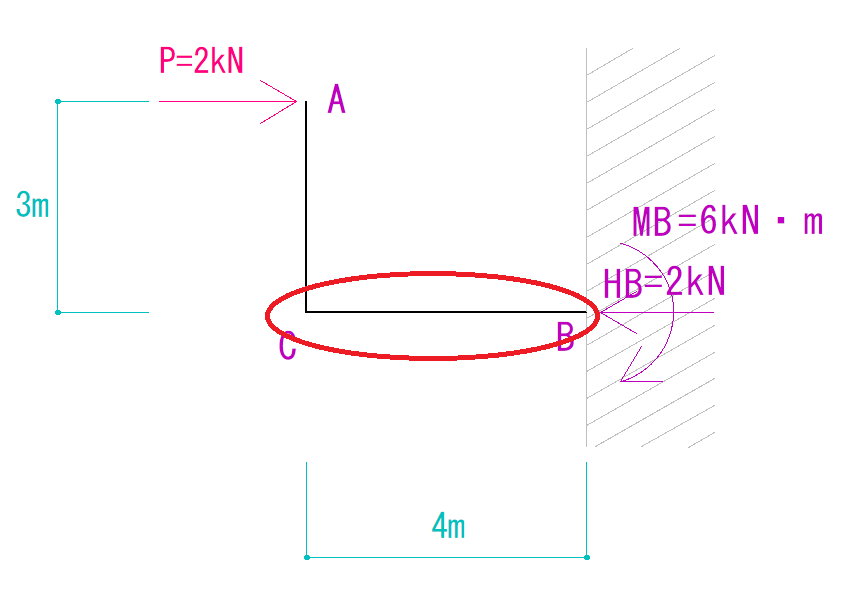
これを見ると、反力として右から左向きにかかる力はありますが、もう片方の側に力がかかっていません。
…ということは、ただ押されているだけで圧縮力や引っ張り力はかかっていないのでしょうか?
そういうことではありません!
荷重に注目しましょう。
荷重はAC間で打ち消されることなく部材を左から右に押しています。
左から右に…つまりCB間の部材の軸方向力です。
イメージとしては下の図のようになります。
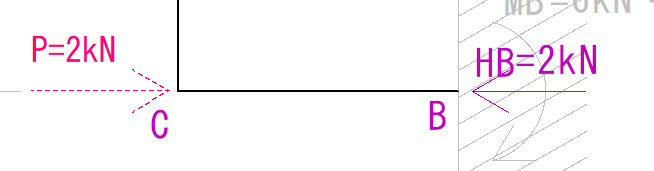
この場合符号はプラスとマイナスどちらでしょうか?
下の表から確認してみましょう。
ということで、符号はマイナス、力の大きさはそのまま2kNとなります。
この圧縮力はCB間で変化することがないので、N図で表すとこうなります。
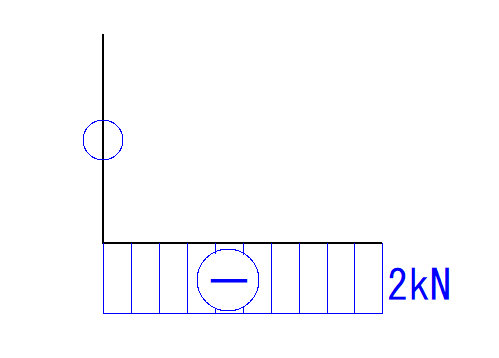
これでN図の完成です。
Q図の描き方
大体のやり方はN図と同様です。
ACとCBに分けて考えます。
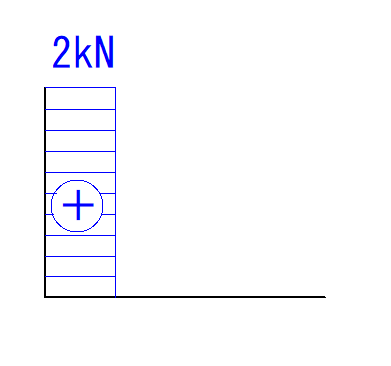
ACのせん断力
ACは荷重がせん断するようにかかっています。
反力もかかっているので、イメージとしてはこのようになります。
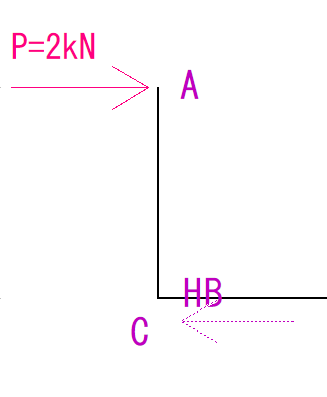
では、これの符号はどうなるのでしょうか?
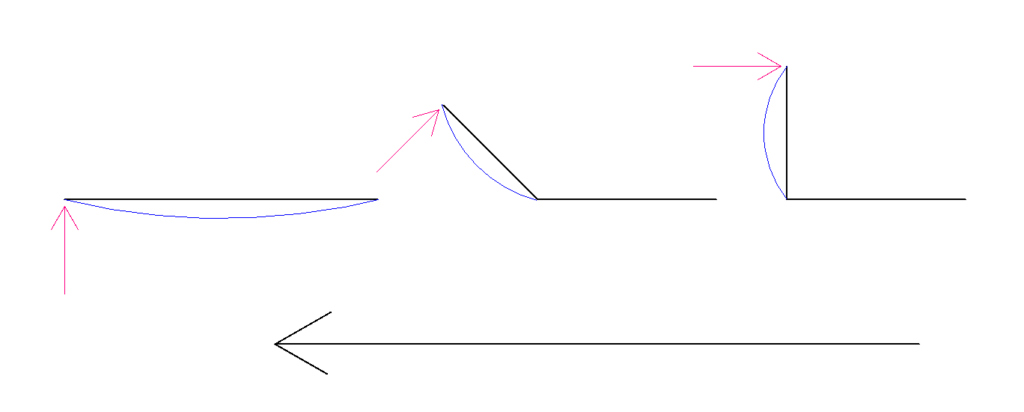
そういう時は頭の中で変形させてまっすぐにします。
言葉ではうまく伝わらないかと思いますので図をご覧ください。

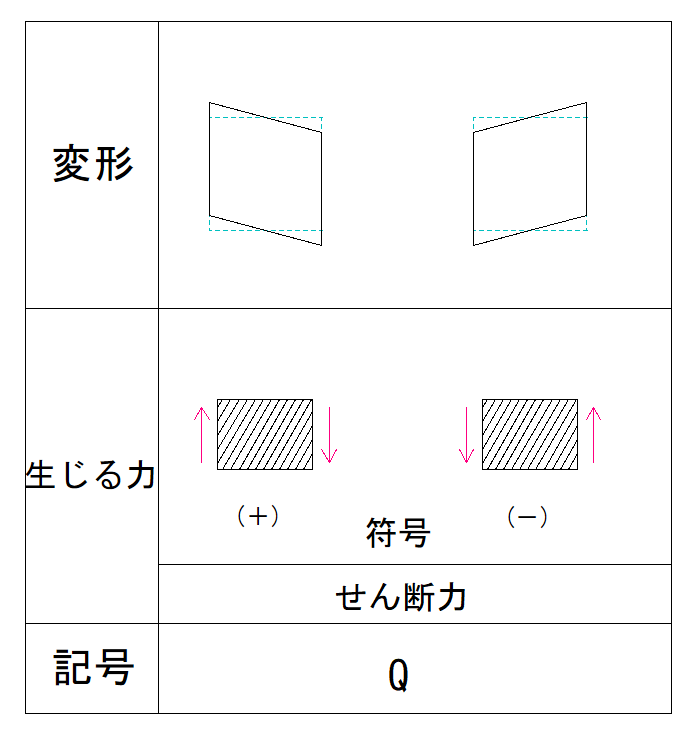
このように考えるとAC間の符号はプラスだということができます。
Q図の符号も先程と同様、まっすぐにした時のイメージを曲げて考えるので、下の図のようになります。
参考
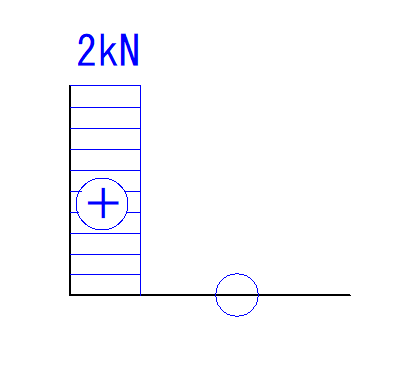
CBのせん断力
次にCBに注目します。
見てわかる通りCBをせん断する力はありません。
よって0になります。
これでQ図の完成です。
M図の描き方
M図の場合はやり方が少し変わります。
A点C点B点のそれぞれのモーメント力を調べ、それを線でつなぎます。
ではやっていきましょう。
まずはA点のモーメント力です。
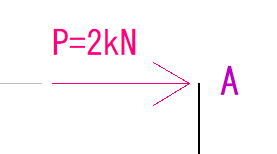
荷重がかかっていますが距離が0なのでモーメント力も0になります。
次にC点です。
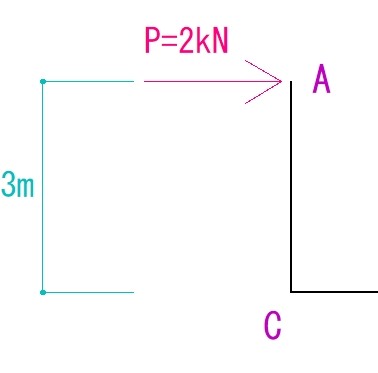
荷重が2kN、荷重との垂直距離が3mなので、モーメント力は6kN・mとなります。
符号の考え方はこれまでと同様です。
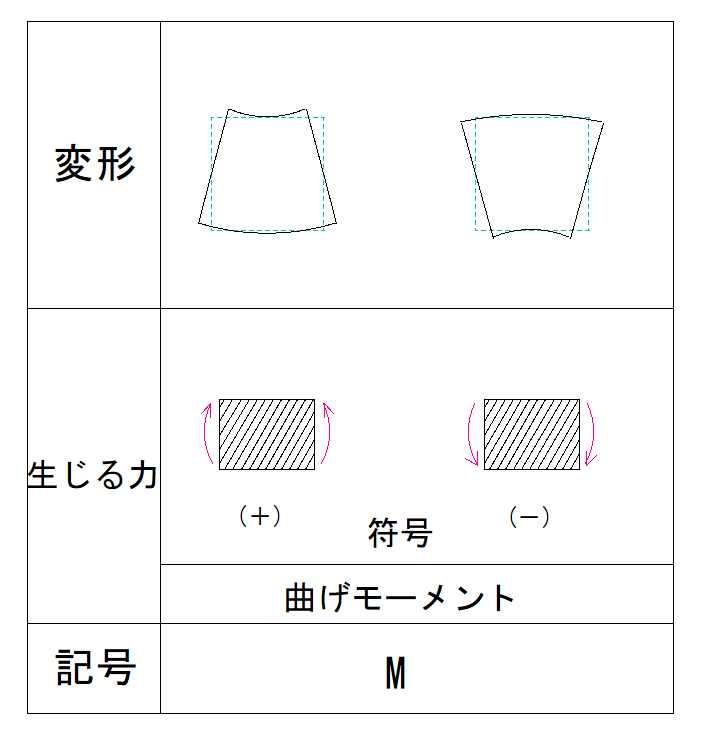
下側が出る、つまり符号はプラスです。
片持梁系ラーメンではこのようになります。
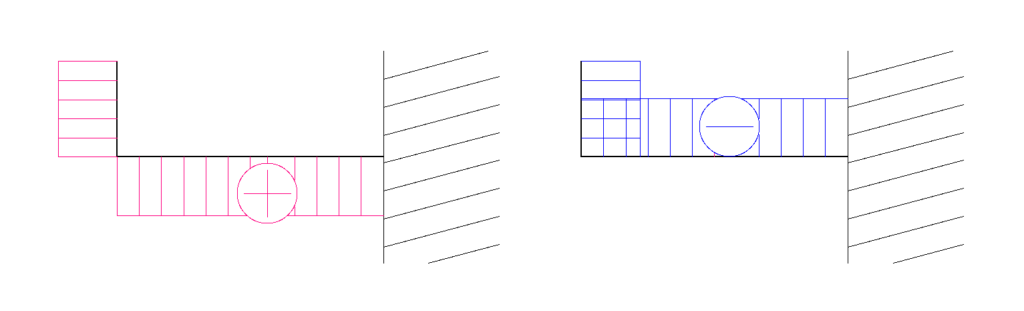
よってこのように描くことができます。
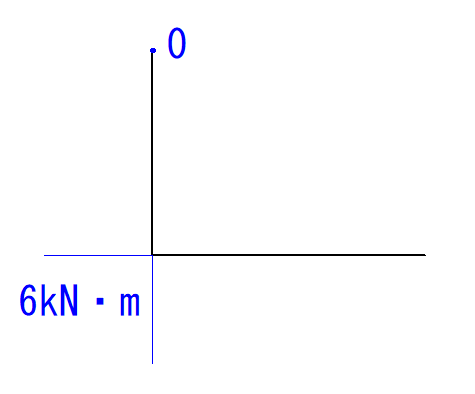
最後にB点です。
B点のモーメント力もC点と同様に計算すると、6kN・mとなります。
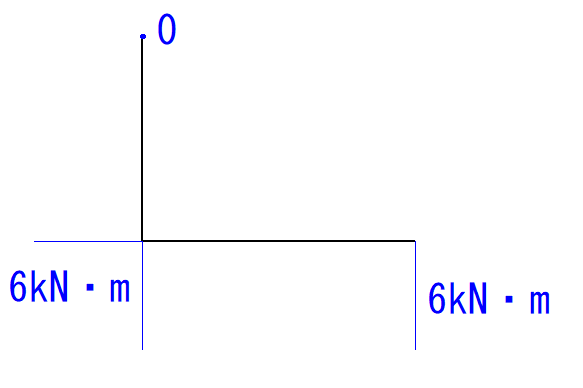
荷重との垂直距離が変わらないためB点とC点のモーメント力(CB間のモーメント力)は変わりません。
最後にそれぞれを線で結びます。
これでM図の完成です。