この記事はTwitterから寄せられた質問に答えるものです。
興味ある方は下のリンクの記事をご覧ください。

まずは問題の写真を見てみましょう。
問題

この写真から図を用意しました。
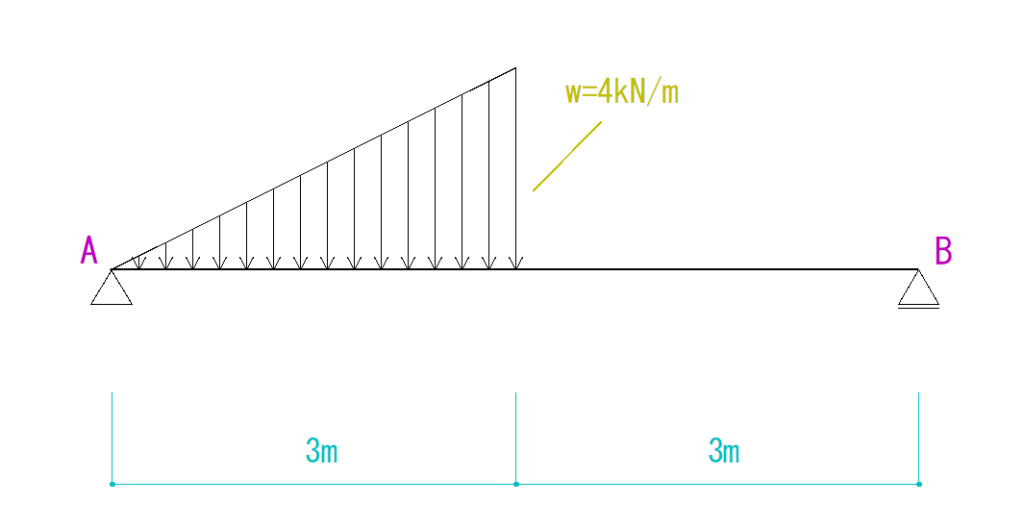
解説
この問題を解くには等変分布荷重について理解する必要があります。
等変分布荷重についての詳しい解説は下のリンクの記事をご覧ください。
では、問題の解説をしていきたいと思います。
まず、等変分布荷重のままではVA、VBを求めることはできません。
等変分布荷重の全部の大きさ(合力)と、その合力がかかる位置を求める必要があります。
等変分布荷重の合力の求め方は公式です。
しっかりと覚えましょう。
等変分布荷重がかかっているところの距離[l]×等変分布荷重の最大厚さ[w]÷2
実はこれは、等変分布荷重の面積を求める式です。

なので公式は三角形の面積を求めるものと一緒になっています。
参考:三角形の公式
底辺×高さ÷2
公式に当てはめて問題を解いてみると
3m[等変分布荷重がかかっているところの距離]×4kN/m[等変分布荷重の最大厚さ]÷2
=6kN
となります。
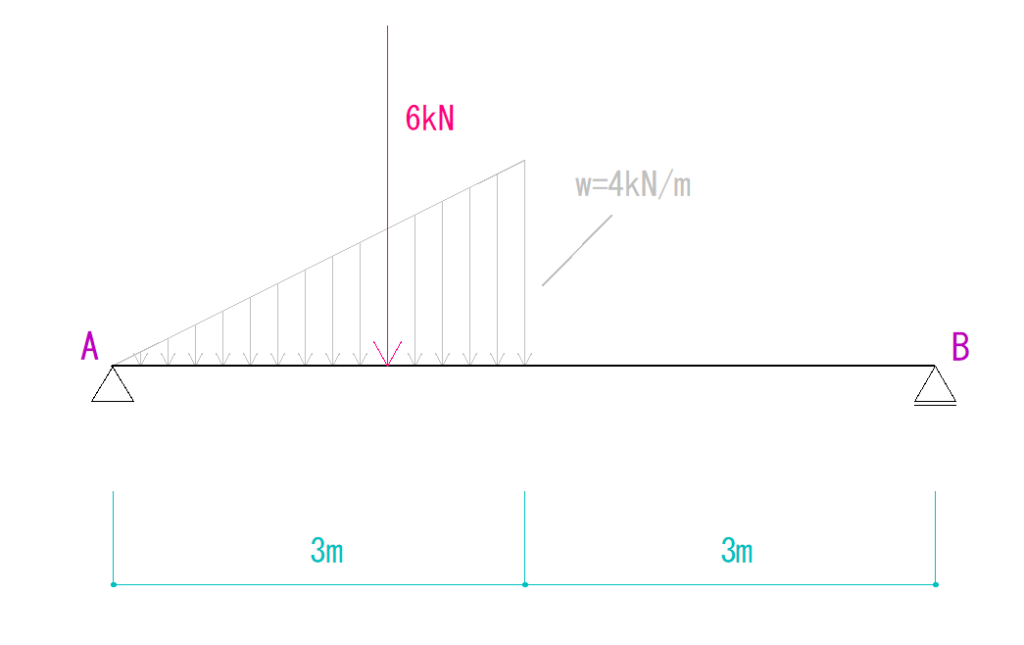
次に合力がかかる位置について考えましょう。
これも決まっています。
それは
等変分布荷重の三角形の重心
です。
「重心」と聞くとよくわからないかもしれませんが、直角三角形の場合下のようになる、と決まっています。
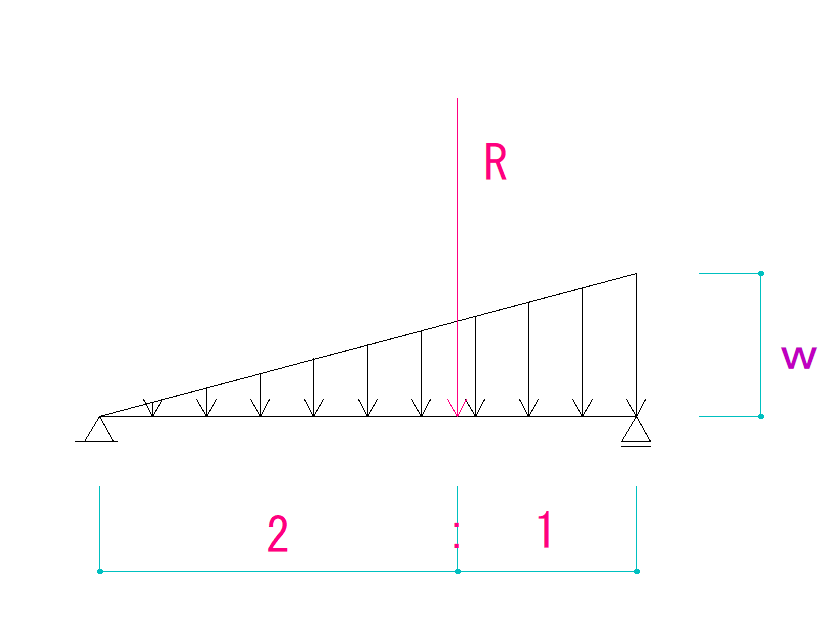
鋭角の方から2:1の場所です。
今回の問題では、A点から右に2mの場所だということが分かります。
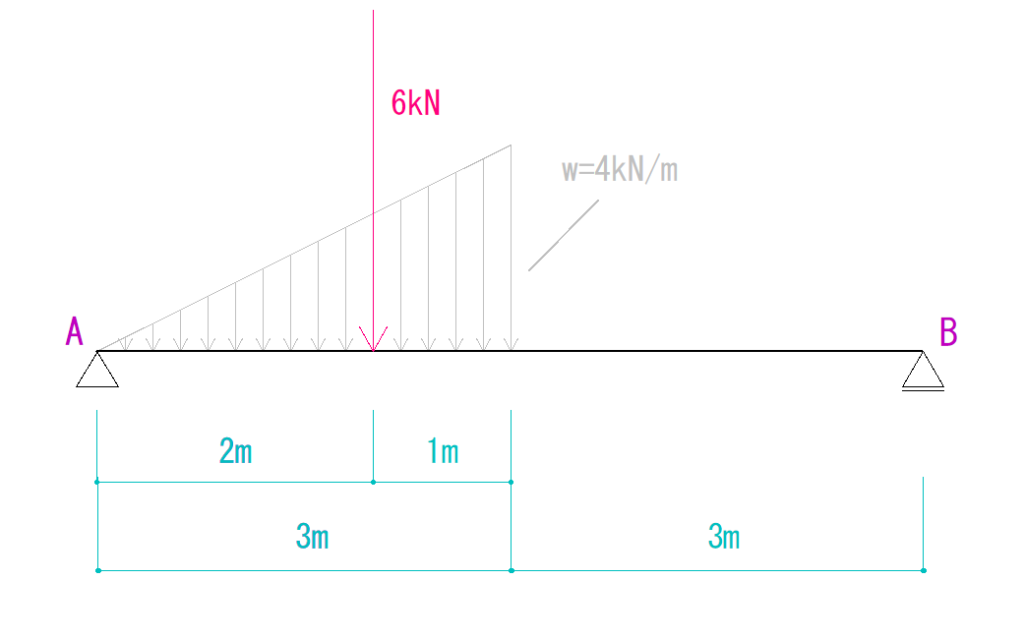
ここまでくれば、後は反力を仮定し釣合い条件で解くことができます。
最初に反力を下のように仮定します。
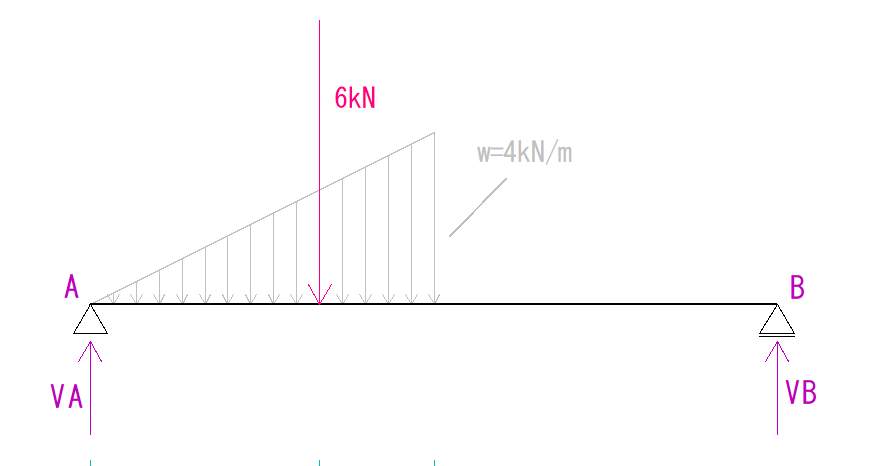
まず、A点をO点とします。
力の釣合い条件より、
ΣRM=0
分力がO点を回す力+合力がO点を回す力=0
になるので、
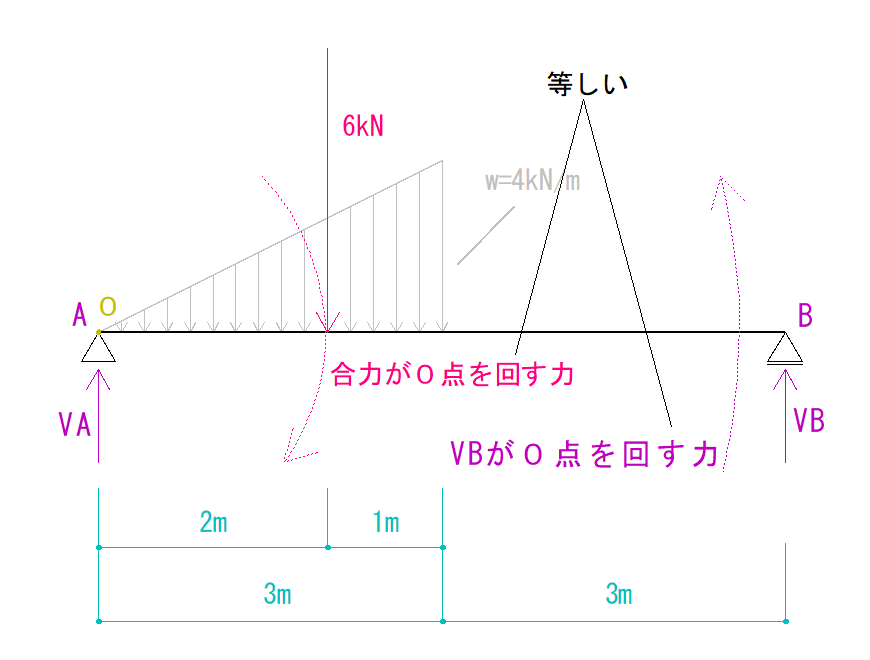
VA×0[距離]+(-VB×6m[距離])+6kN[合力]×2m[距離]=0
仮定したVBの向きはO点を反時計回りに回すのでマイナスが付きます。
式を解いていくと、
-6VB+12=0
VB=2kN(仮定通り上向き)
となります。
上からの荷重が6kNでVBで2kN支えているので、残りをVAで支えないといけません。
6-2=4
VA=4kN(仮定通り上向き)
となります。
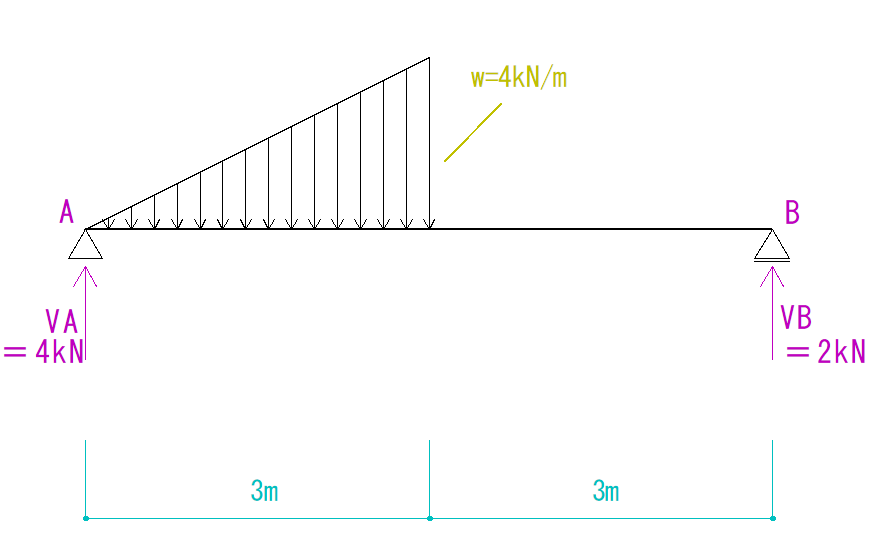
解答
VA=4kN(仮定通り上向き)
VB=2kN(仮定通り上向き)
荷重に水平反力が生じていないためHA=0