この記事はTwitterから寄せられた質問に答えるものです。
興味ある方は下のリンクの記事をご覧ください。

今回は軸方向力のx地点における断面力の計算について解説していきたいと思います。
問題
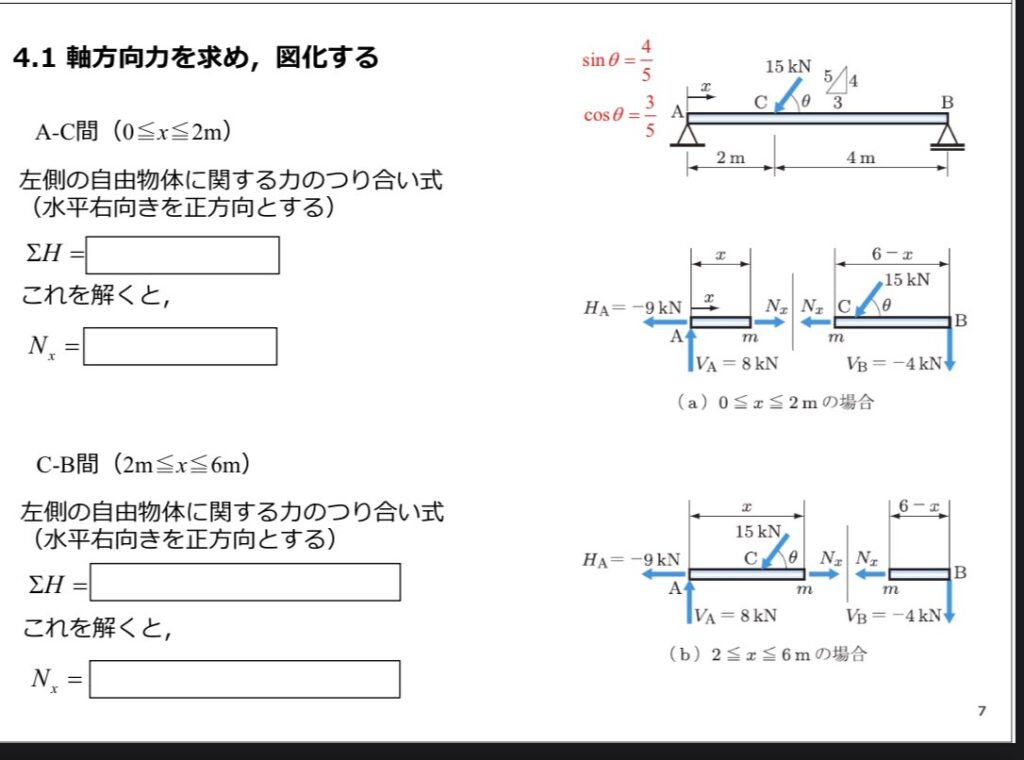
解説
まずはこの問題の図から考えていきたいのですが、HA、そしてVBを見て少し変だな、と感じるかもしれません。
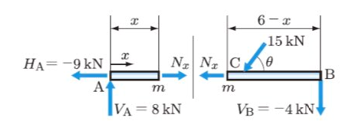
なぜなら荷重は斜め左下に向かってかかっています。
そう考えると、
反力は荷重の左に対して右向き
そして荷重の下に対して上向きになるはずだからです。
さて、ここからはやり方の問題になってきます。
教授のやり方、教科書のやり方、参考書のやり方、等々色々な方法がありますので、ご自分が得意なやり方を見つけるのがいいと思います。
今回は、反力の向きを重視しながら解く方法を解説いたします。
HA、そしてVBをよく見ると、値にマイナスが付いています。
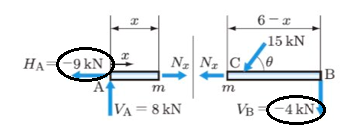
つまり、
左向き-9kN=右向き9kNというわけです。
VBも同様に下向き-4kN=上向き4kNです。
なぜこんなややこしいことになっているかというと、応力の符号をプラスで仮定することを重視したためと考えられます。
参考
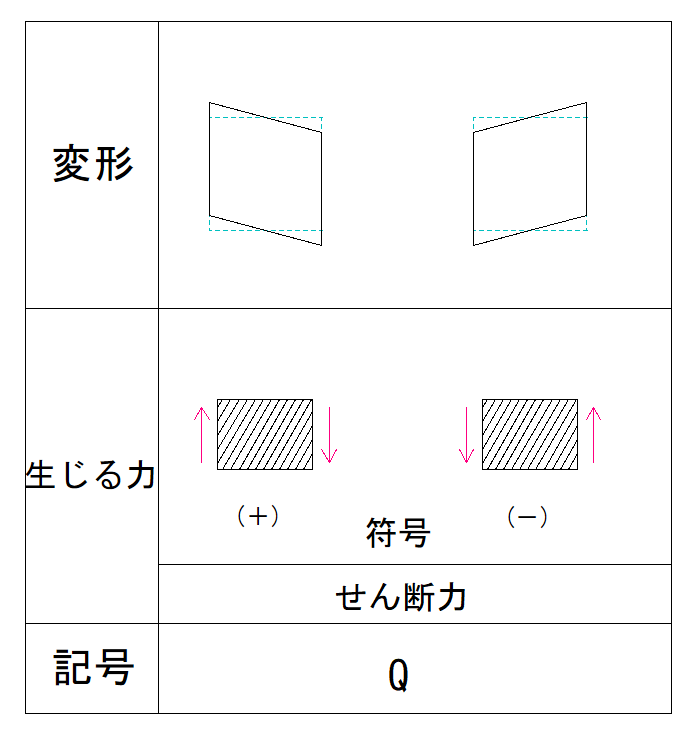
ただ、結局計算するときは右向き、上向きで計算する必要があるので今回は戻しておきたいと思います。
(a)の問題
では最初の穴埋めからしていきます。
xの定義が
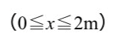
の時のことを考えましょう。
つまり、AC間にx地点があった場合の断面の軸方向力を求めよ、ということです。
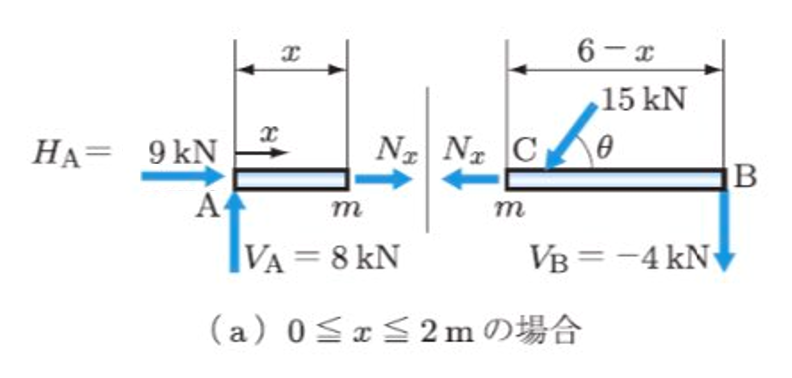
図で表すとこの部分になります。
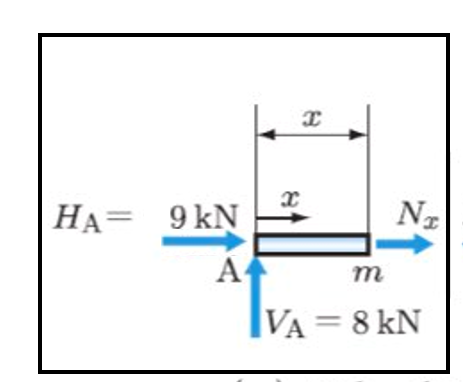
断面力にかかる軸方向力は分からないのでNxとされています。
ここで注意点です。
今回は前もって仮定されていますが、自分で仮定するときは断面にかかる応力の仮定の向きはプラス方向(応力の符号で)にしましょう。
その方が分かりやすくなってケアレスミスが減ります。
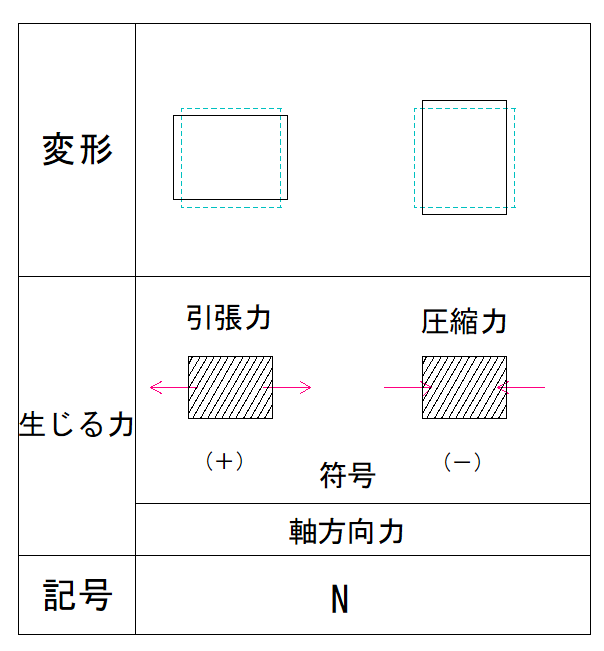
※応力の符号と力の符号は別物なので注意しましょう
参考

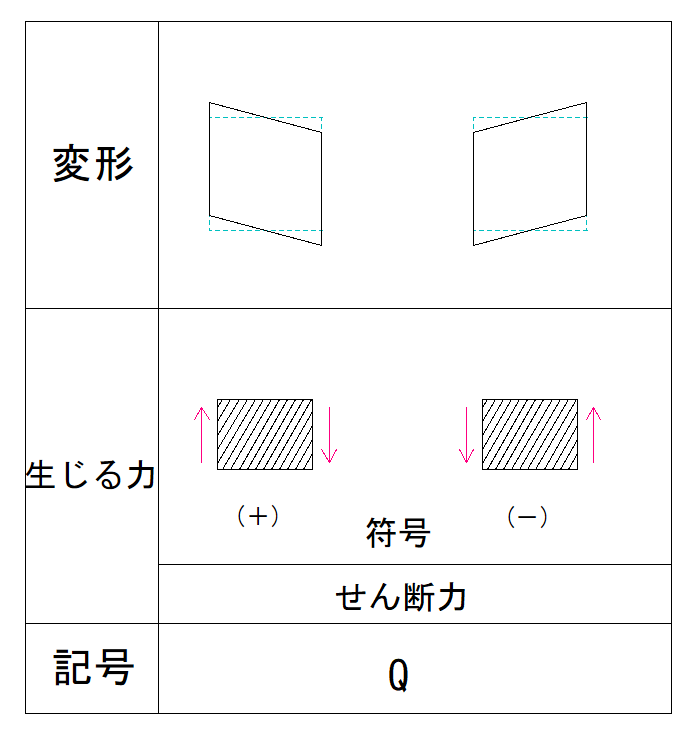
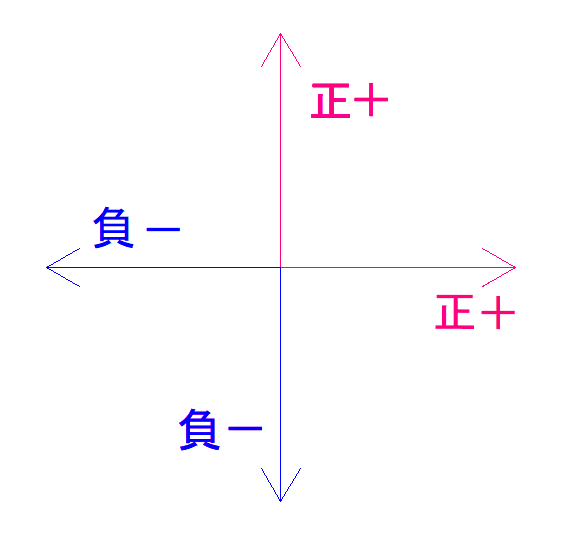
力の向きの符号
さて、穴埋めの前がΣHとなっているので、水平方向の力をピックアップしていきます。
ここでの符号は力の向きの符号です。
まずは、反力の+9kNです。
(左向き-9kNを無理やり使うとすれば「-(-9kN)」となります。)
そして+Nx
のみとなっています。
式はΣH、つまり水平方向の総和ですので足してあげます。
9 + Nx
そして、釣合っている物体の応力の和は0になる必要があるので「=0」としてあげましょう。
9 + Nx = 0 (穴埋めの答え)
(もしくは-(-9) + Nx = 0)
Nx=-9kN (穴埋めの答え)
となります。
符号がマイナスになったのでNxの向きが仮定とは逆、左向きになるということが分かりました。
また、軸方向力は圧縮力になります。
(b)の問題
次にxの定義が
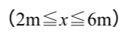
の時のことを考えます。
つまり、CB間にx地点があった場合の断面の軸方向力を求めよ、ということです。
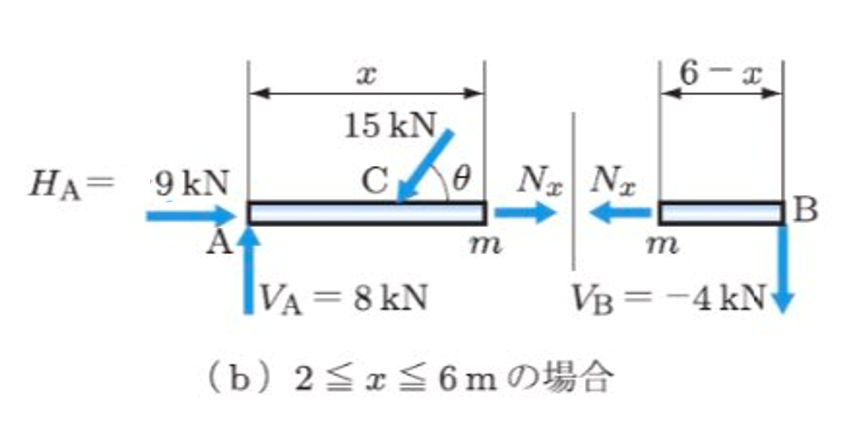
図で表すとこの部分になります。
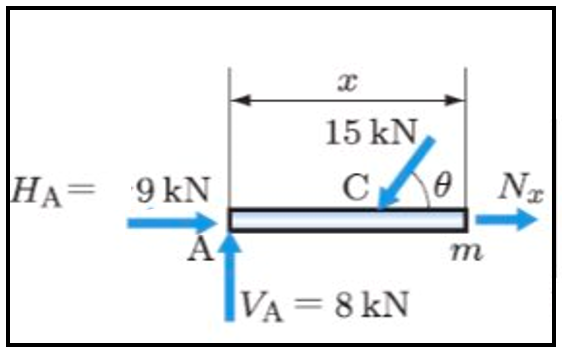
これも先程と同様の仕方で解いていくことができます。
ΣHですので水平方向の力をピックアップします。
ここでの符号は力の向きの符号です。
まずは反力+9kN
(左向き-9kNを無理やり使うとすれば「-(-9kN)」となります。)
そして荷重-(15×cosθ)
最後に+Nx
これらを足します。
9 + (-15×cosθ) + Nx = 0 (穴埋めの答え)
(もしくは-(-9) + (-15×cosθ) + Nx = 0)
9 + (-9) + Nx = 0
0 + Nx = 0
Nx = 0 (穴埋めの答え)
よって、CB間には部材内に軸方向力はかかっていないということが分かります。
もしかかっていたとしたら、B支点にも水平反力必要になりますもんね。
さて、ここまで解説してきましたが、構造力学のアプローチは色々あります。
それで、学校でやるやり方と差異が出てしまうかもしれませんが、結局の答えは同じところにたどり着くので参考までに理解していただくと嬉しいです。



