この記事はTwitterから寄せられた質問に答えるものです。
興味ある方は下のリンクの記事をご覧ください。

トラスの解き方には「節点法」とは別に「切断法」というものがあります。
「節点法」では、各節点を一つずつ考えて、部材一つ一つにかかる力の向きと大きさを考えました。
「切断法」はそれとは少し違う考え方をします。
「切断法」では、指定された部材(多くの場合が3つの部材)にかかる力と大きさを求めていきます。
それでは早速考えていきましょう。
例題
下の図のトラスの①②③材の軸方向力を切断法によって求めなさい。
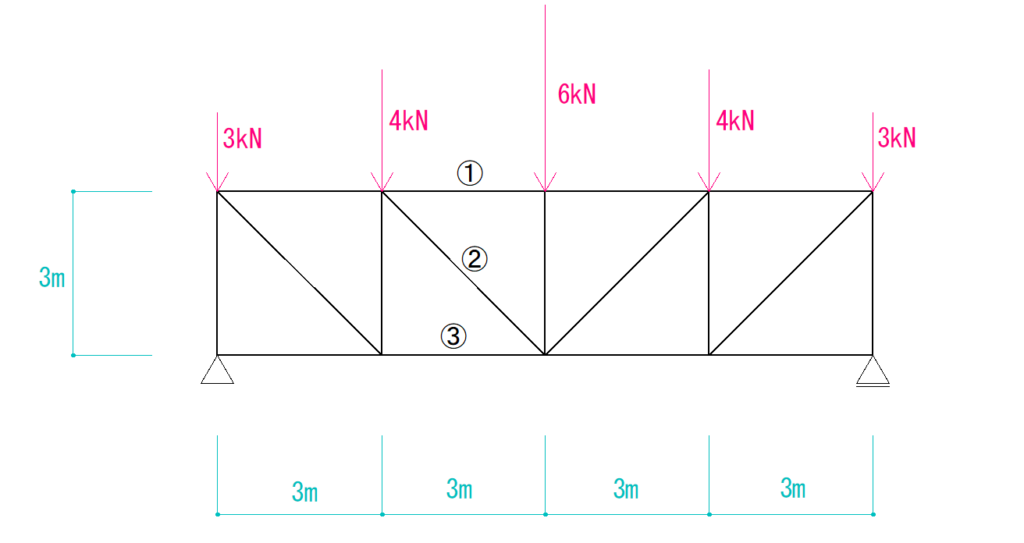
解説
反力の決定
まず、反力を求めます。
このトラスの形は左右対称で、かかっている荷重も左右対称なことから、総荷重の半分が支点にかかってくるとわかります。
つまり、
3+4+6+4+3=20kN
20÷2=10kN=VA=VB
となります。
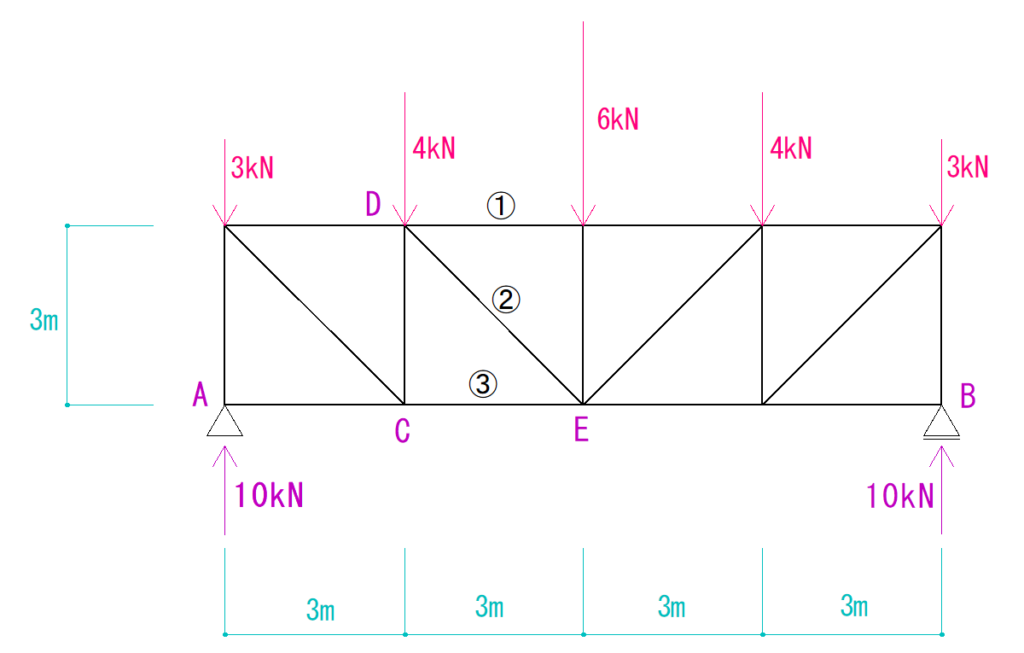
軸方向力の計算
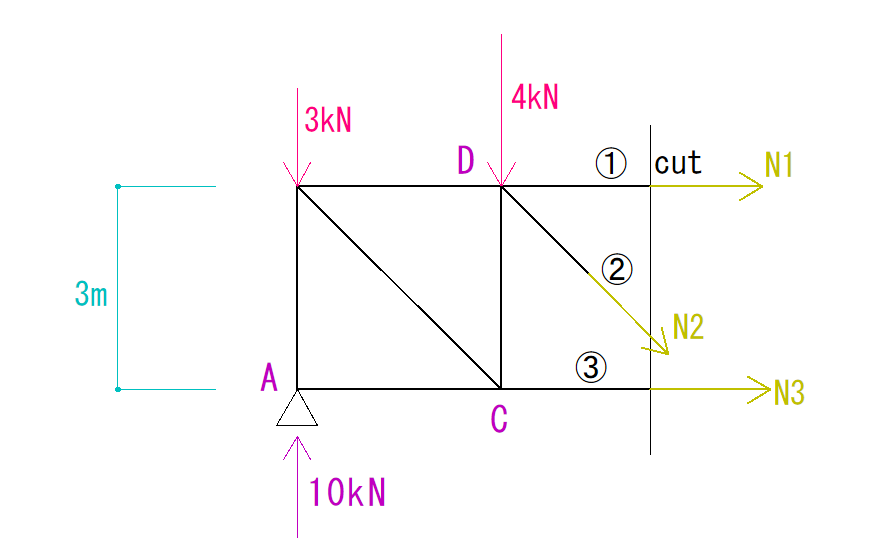
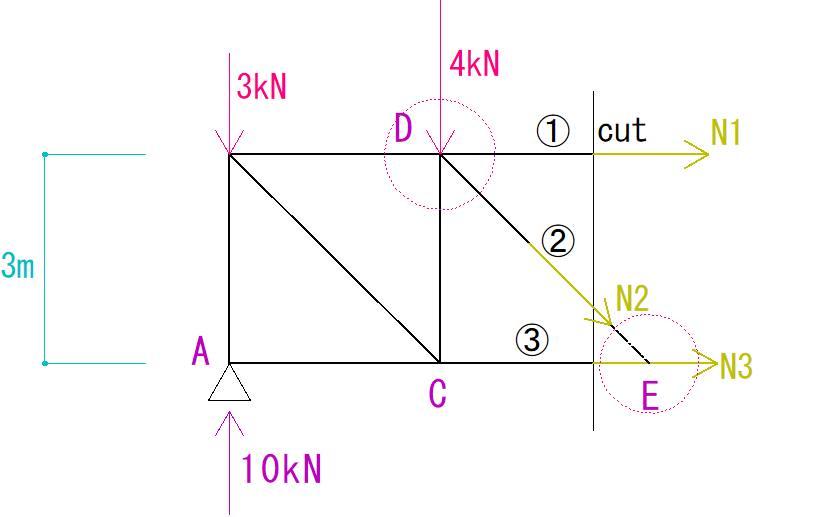
まず、指定されている3つの部材を通るように切断し、その左側(右側でも可)を見ます。
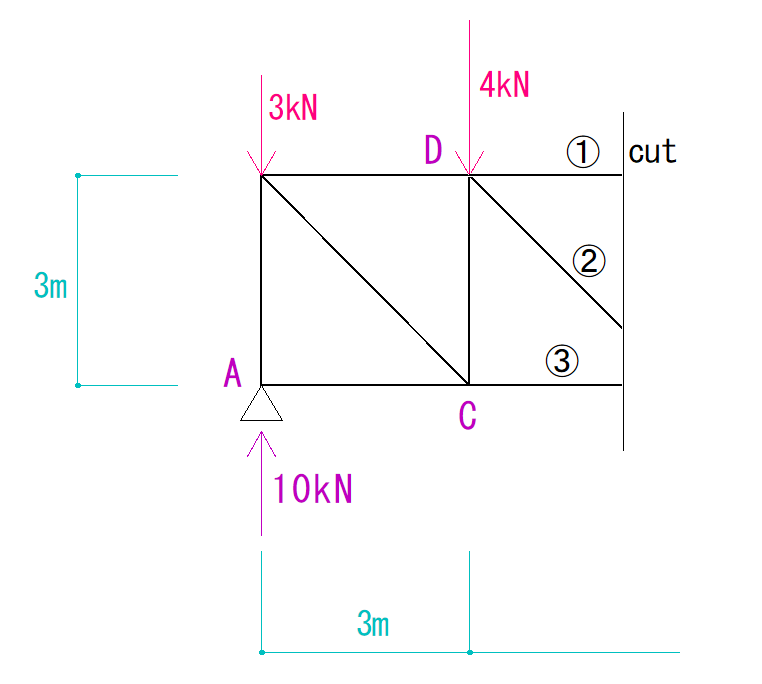
注意点
この問題ではスムーズに3つの部材を通るように分けることができましたが、下のような問題の場合どうでしょうか?
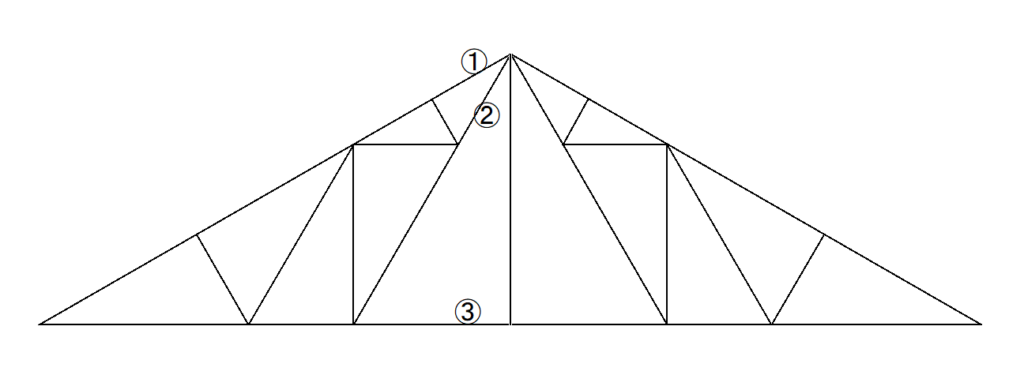
切り方によっては、部材を4つ5つでも切れてしまいます。
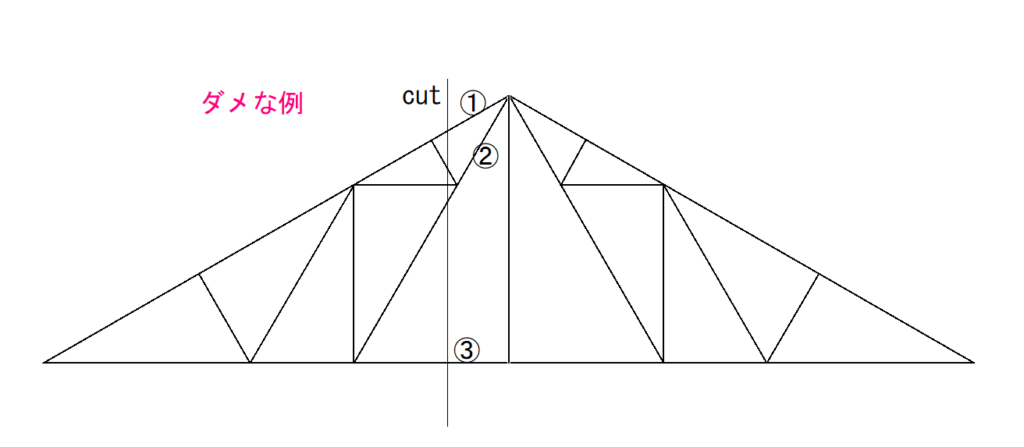
しかし、切断法は部材を3つまでしか切ってはいけません。
(3つ以上だと値を求めることができなくなります)
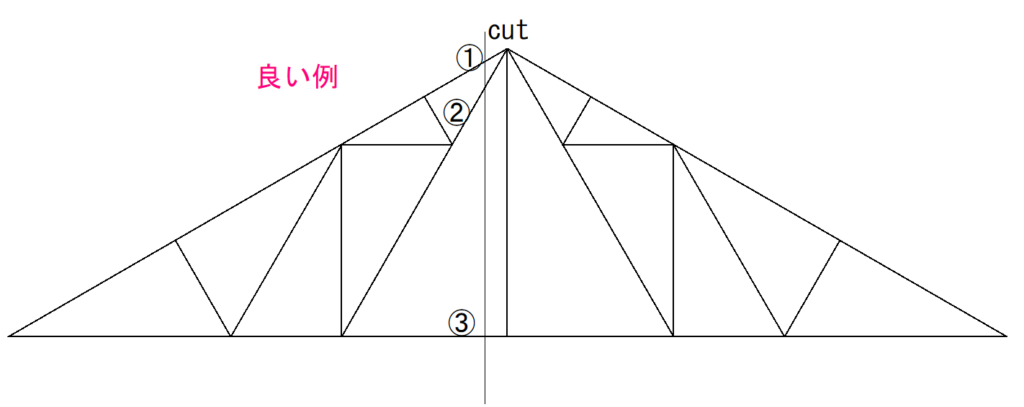
そこまでひねくれた問題はあまり出ないとは思いますが、うっかり部材を多く切ってしまって、訳分からなくなることがないようにしましょう。
本題に戻ります。
これから計算をしていきますが、前提として、釣合っているトラスはどこで切っても、外力と軸方向力は釣合っています。
つまり、
①②③の軸方向力の合力 = 外力(荷重、反力)
ということです。
では、ΣX、ΣY、ΣMをそれぞれ考えていきましょう。
最初に、計算のため軸方向力の向きを仮定しておきます。
①の軸方向力をN1
②の軸方向力をN2
③の軸方向力をN3
とします。
X方向の力の解法
外力はX方向に力が加わっていません。
つまり、①②③の軸方向力だけを計算すればよいということになります。
式に表すと
ΣX=0より、
N1 + N2 sin45°(N2をX方向に分解した力)+ N3 = 0 …☆
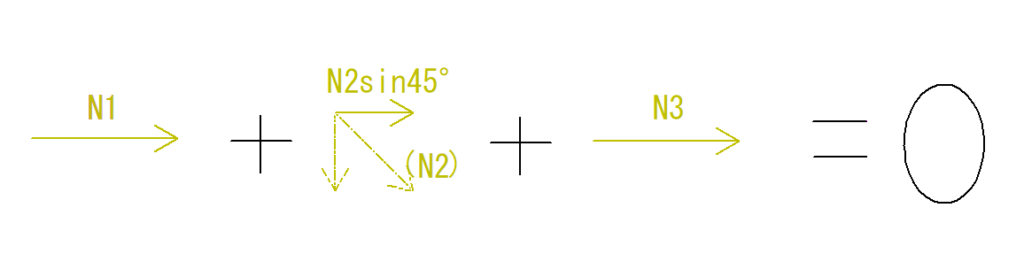
となります。
これだけでは計算ができないので、この式はとりあえずこのままにして次に進みます。
Y方向の力の解法
Y方向にかかっている力は、外力、そしてN2を分解したときのY方向の力になります。
式を組み立てると、
ΣY=0より、
10 + (-3)+(-4)+(-N2cos45°(N2をY方向に分解した力))=0
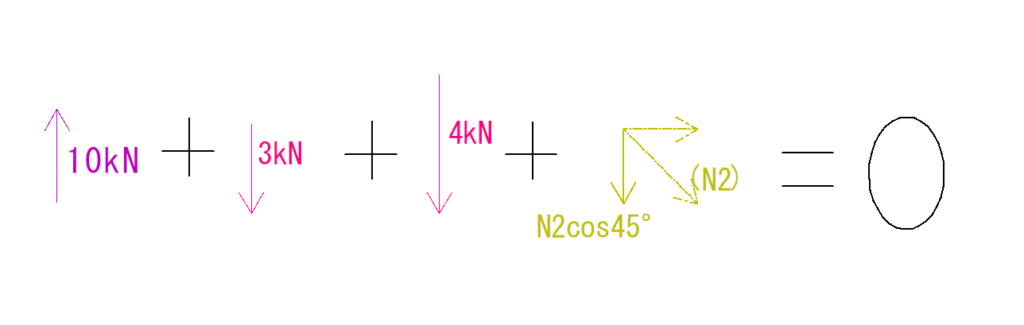

となります。
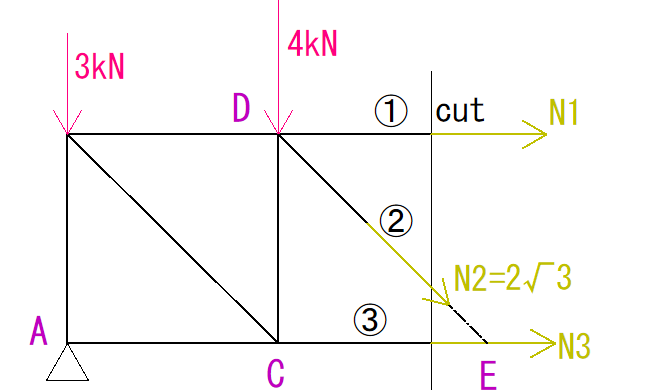
モーメントの解法
トラスはどこで切っても、どの地点でも力が釣合います。
なので、どこに点を取ってもΣM=0になりますが、少しでも計算を楽にするために、部材①②③のうち二つの作用線がぶつかっているところを指定します。
今回の場合、D点もしくはE点です。
どちらを使っても大丈夫ですが、解説ではD点を用います。
式で表すと、
ΣMD=0より、
10[VA]×3[VAとDの距離]+(-3[A点の荷重]×3[荷重とDの距離])+(-3[N3とDの距離]×N3)=0
(N1、N2、荷重の4kNは距離0の為、モーメント力も0となります。)
30-9-3×N3=0
-3×N3=-21
N3=7kN
となります。
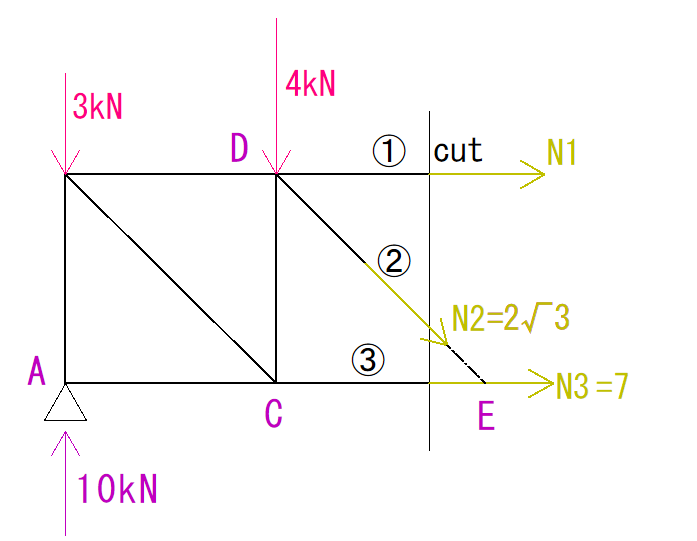
最後に、ΣX=0の時の式(☆の式)に分かった値を代入していきます。
N1 + N2 sin45°(N2をX方向に分解した力)+ N3 = 0より、
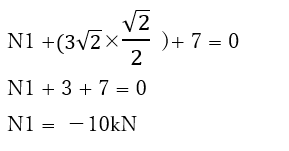
となります。
符号がマイナスなので仮定の向きとは反対方向ということが分かります。
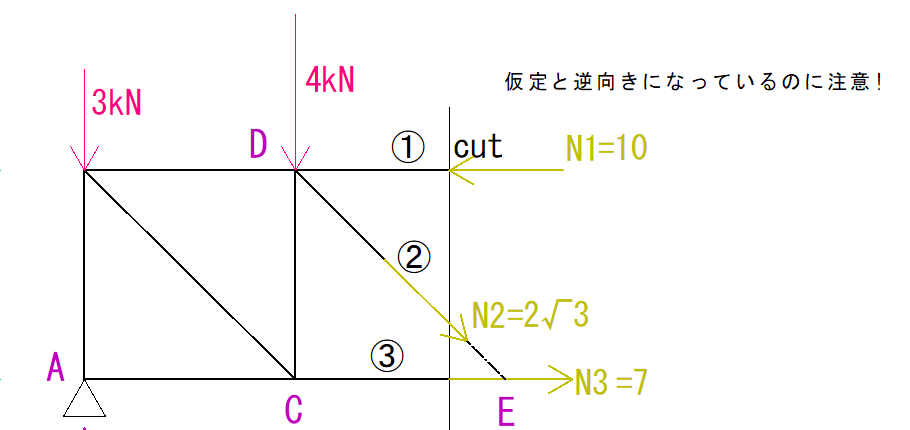
解答

となります。
まとめ
切断法は理解してしまえば、難易度は高くない分野になっています。
ただ応用問題になってくると、図や角度が複雑化してきます。
基本のやり方は一緒なので、落ち着いて一つ一つをこなしていきましょう。

