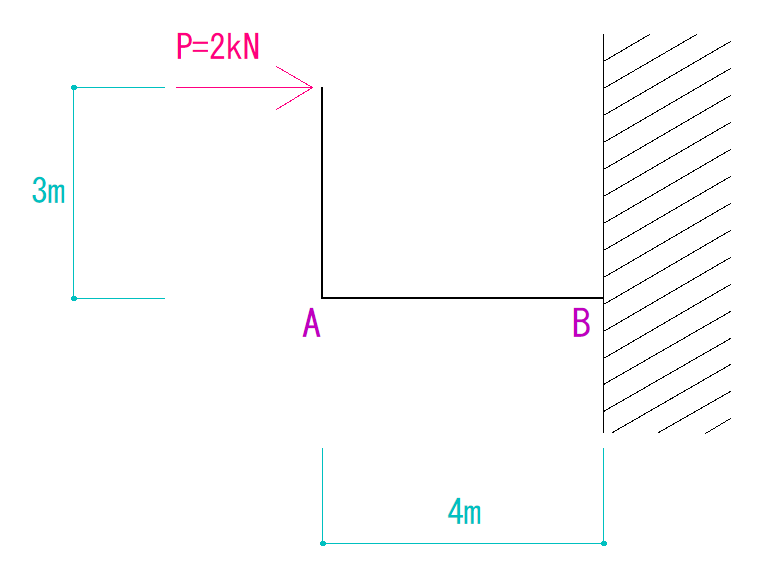
今回はラーメン構造の反力の求め方第2回ということで、単純梁系ラーメンの反力の求め方を解説していきたいと思います。
ラーメン構造について、また先回の片持梁系ラーメンの反力の求め方については下のリンクの記事を参照ください。
では早速例題を使って考えていきましょう。
例題
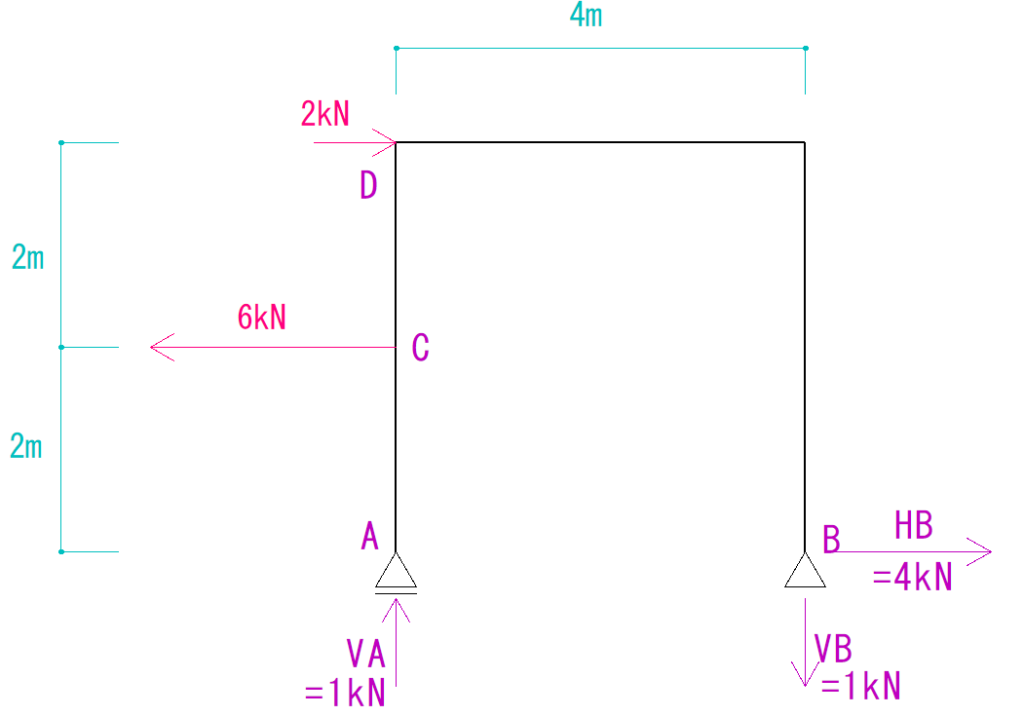
下の図を見て反力をそれぞれ求めなさい。
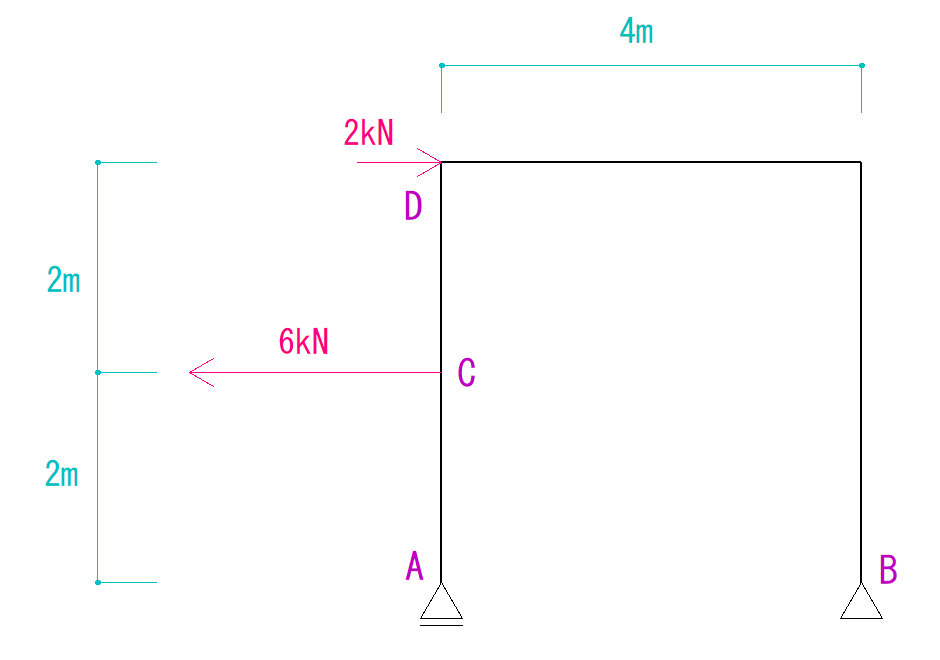
解説
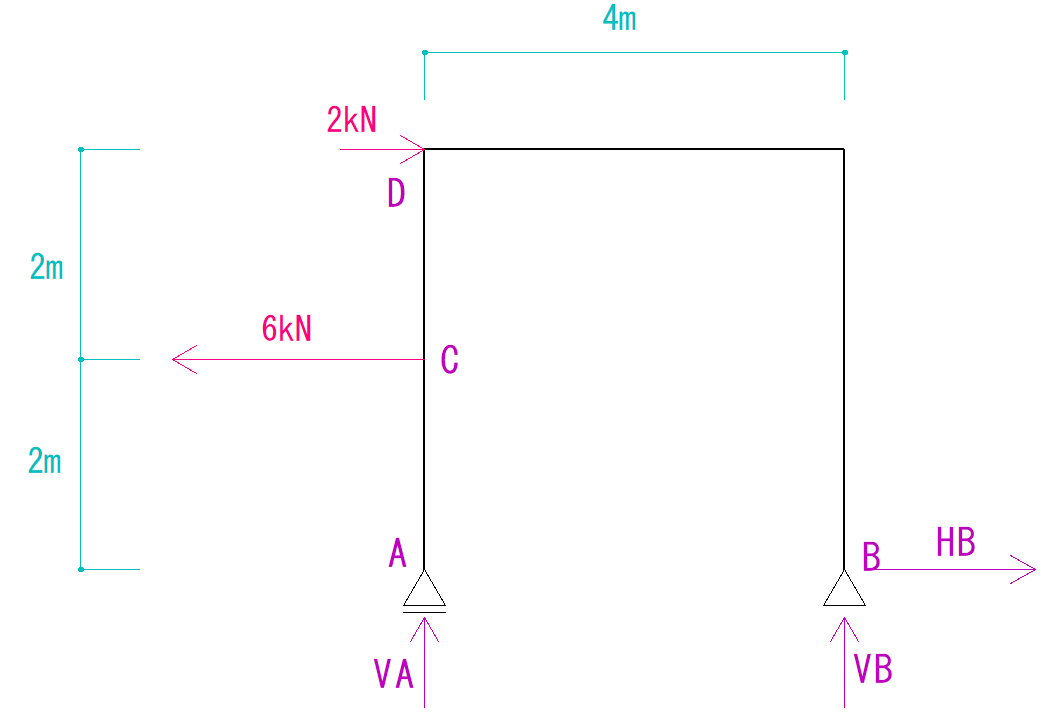
反力の仮定
支点を見ると移動支点と回転支点となっています。
よって発生する反力は下の図のようになります。
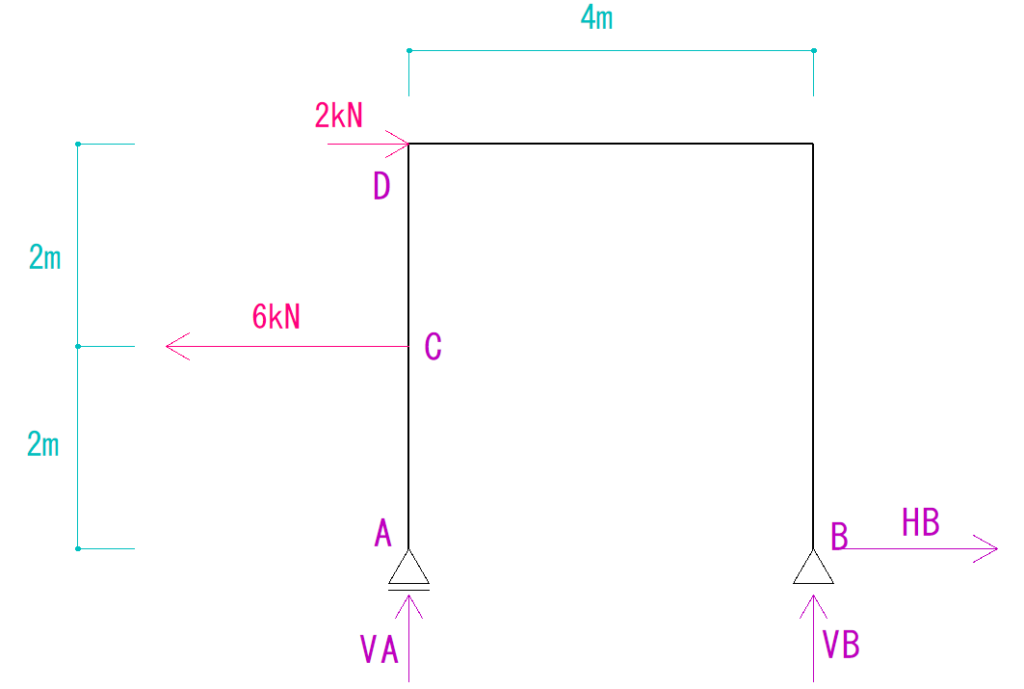
支点にかかる反力については下のリンクの記事を参照ください。
力の釣合いから求める
後はそれぞれの力の釣合い条件を考えます。
一つずつ考えていきましょう。
ΣX=0
まず、X方向にかかっている力だけを見てみましょう。
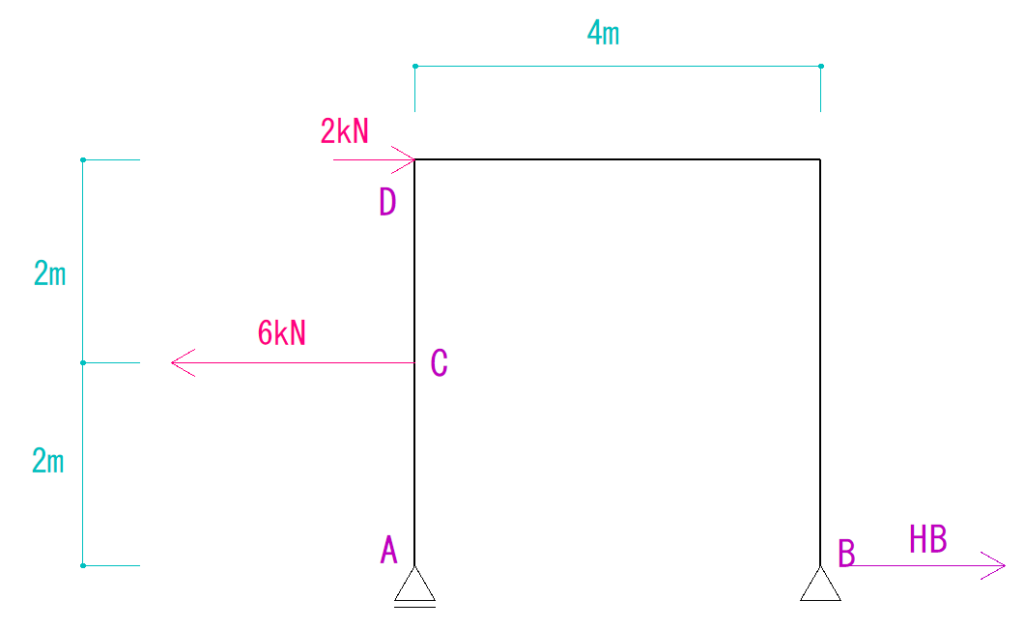
そうしたら全部を足して答えが0になるようにします。
2kN + (-6kN) + HB =0
-4kN +HB = 0
HB = 4kN
答えにプラスが付いたということは仮定の向きで合っているということが分かります。
よって、
HB = 4kN(右向き)
となります。
ΣY=0
Y方向にかかっている力を見てみましょう。
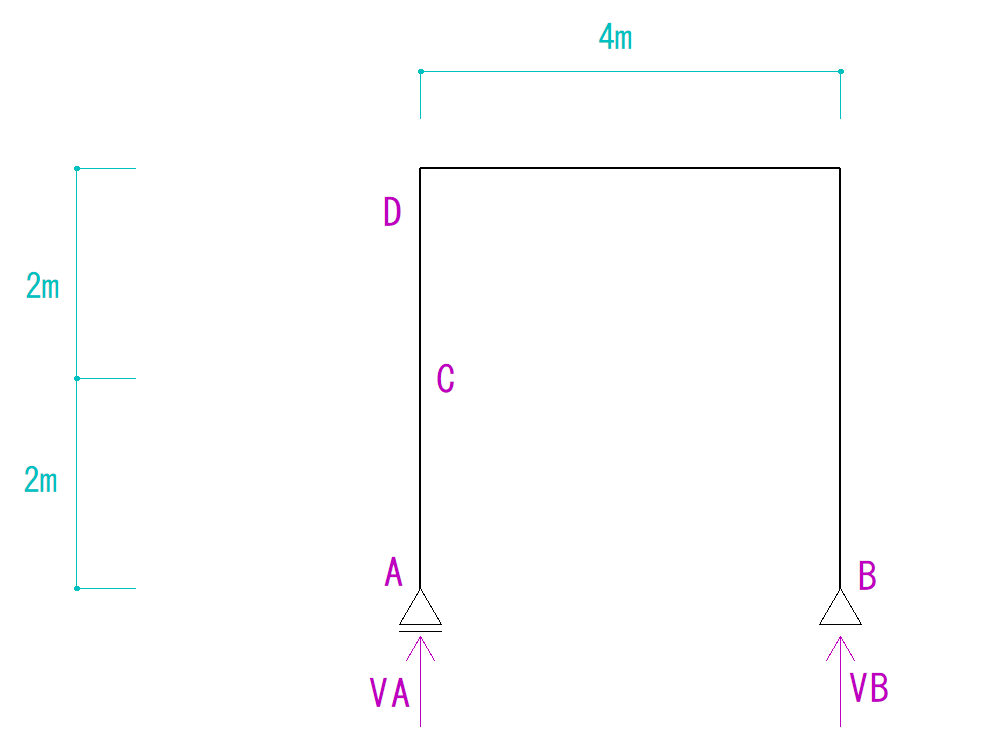
VAとVBだけになります。
Y方向への荷重はかかっていないので、
VA=0
VB=0
となります。
…が!ここで注意です。
これはまだ仮定の状態です。これが答えにならないので気を付けてください。
ΣM=0
モーメント力を見てみましょう。
今回はA点を支点(O点)とします。
この問題では直接モーメント荷重はかかっていませんが、それぞれの力はA点を回す力を持っています。
そして単純梁系ラーメンでは、最初に荷重でのみのモーメント荷重を求めます。
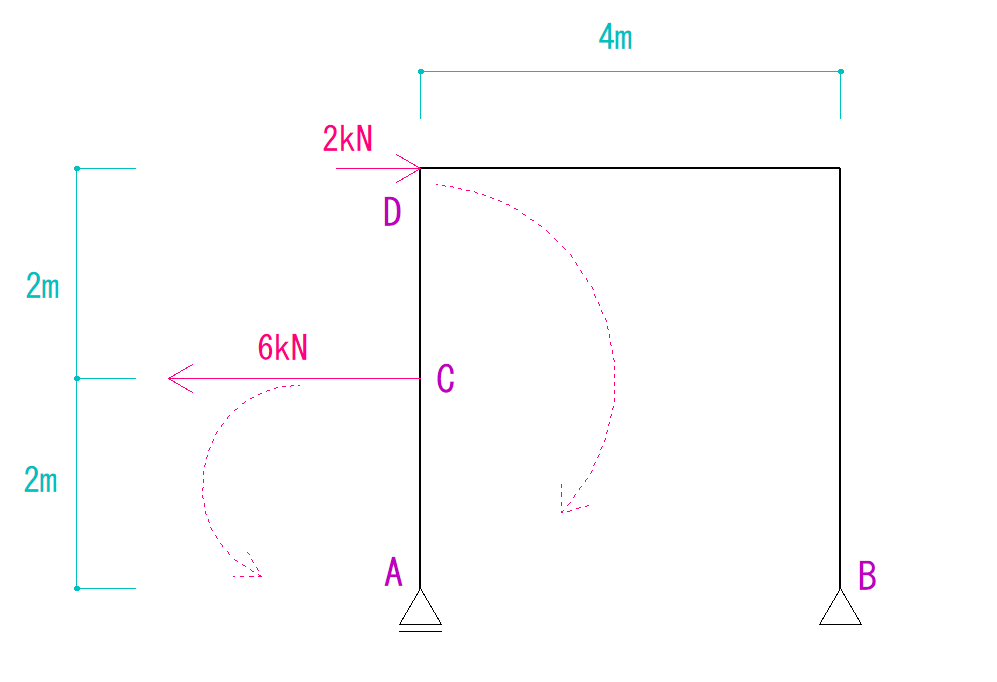
実際にやっていきながら解説してきます。
まず、それぞれのモーメント力を足していきます。
2kN × 4m +(- 6kN × 2m)
※モーメントの向きによってマイナスをつけるのを忘れないようにしましょう。
=8kN・m - 12kN・m
= -4kN・m
となります。
これで分かるのは荷重がどのくらいの大きさでこのラーメンを回そうとしているか、ということです。
今回は-4kN・mの大きさで回そうとしていることが分かりました。

つまり反力で4kN・mの大きさを出さないといけません。
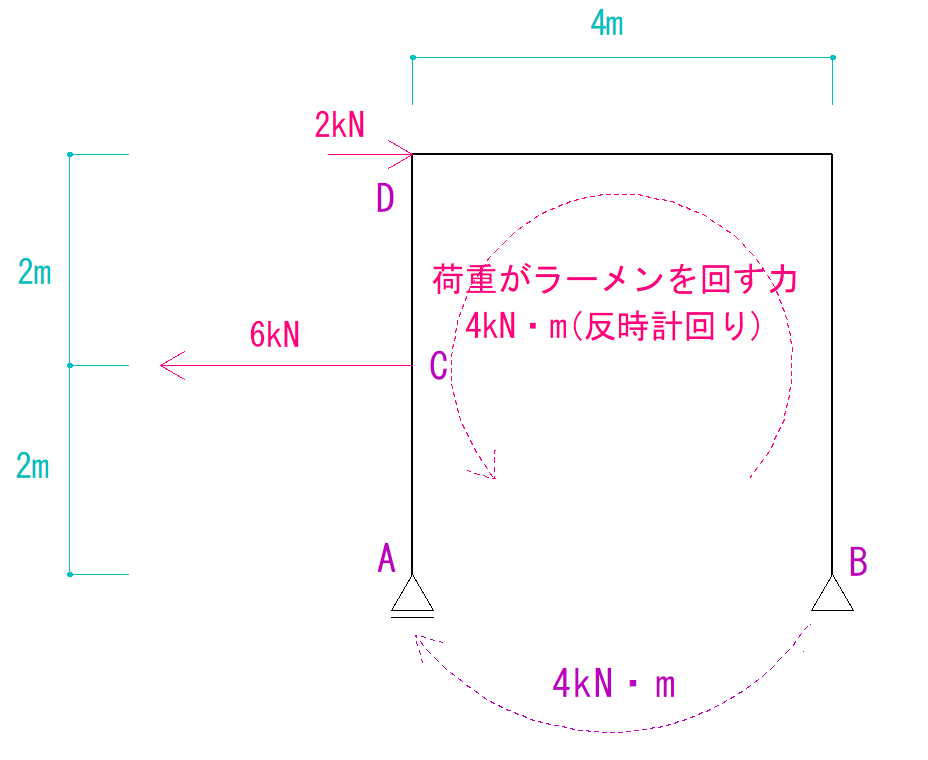
モーメント反力なしでそんなことができるでしょうか?
…できます!
以前に解説した「偶力」を使います。
今回はVAとVBで偶力を発生させることができそうです。
偶力について詳しくは下のリンクの記事を参照ください。
詳しくは以前の記事を見ていただくとして、ここでは公式を復習してさらっといきたいと思います。
M=PL[N・m,kN・mなど]
P…一方の力の大きさ[N,kNなど]
L…2力間の垂直距離[mm,mなど]
この公式に今回の問題を当てはめます。
Mは先程確認したように4kN・mとなります。
PはVA及びVBです。
今回はこの部分を求めます。
Lは問題に書いてある通り4mです。
ここから式を組み立てると、
4kN・m = P × 4m
4 = 4P
P = 1kN
となります。
つまり、
VA=VB=1kN
ということが分かります。
後は偶力によってプラス向き(時計回り)に力がかかるように符号を決めます。

VA=1kN(上向き)
VB=1kN(下向き)
となります。
最後にΣYの時に求めたVA、VBの値と足します。
今回ΣYの時どちらも答えが0だったため値の変化はしません。
VA=-1kN + 0
=-1kN
VB=1kN + 0
=1kN
答え
VA=1kN(上向き)
VB=1kN(下向き)
HB=4kN(左向き)
となります。