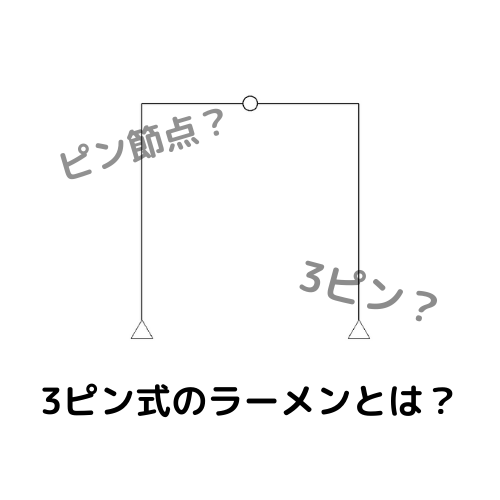
今回は、ラーメン構造の反力の求方シリーズの途中ではありますが、用語説明を行いたいと思います。
3ピン式ラーメンと言われてすぐにピンとくるでしょうか?
「…あーなんかラーメン構造の中に丸い変なのが入ってるやつかぁ…」
ぐらいの理解をしている方もおられると思いますので、今回はその特徴をわかりやすくしっかりの解説していきたいと思います。
「ピン節点」とは?
3ピン式ラーメンの特徴は、ラーメン構造の途中で「ピン節点」が入っていることです。
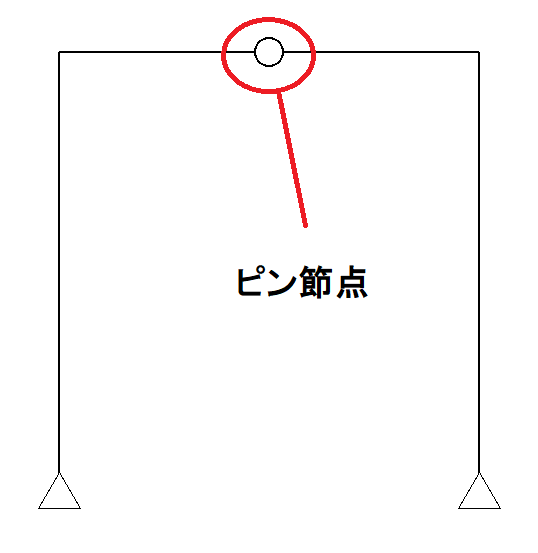
このピン節点とはどういうものでしょうか?
それは、「回転が自由な節点」と定義されています。
イメージとしては蝶番を想像してみてください。
(あくまでもイメージですが…)

実際、「回転が自由な節点」といっても、少しの力で回ってしまうようなものではありません。
ただ、構造上大きな力が加わったとき、安定した形状の維持を期待できない節点ということです。
3ピン式のラーメンの特徴
この「ピン節点」が入っているラーメン構造にはどんな特徴があるでしょうか?
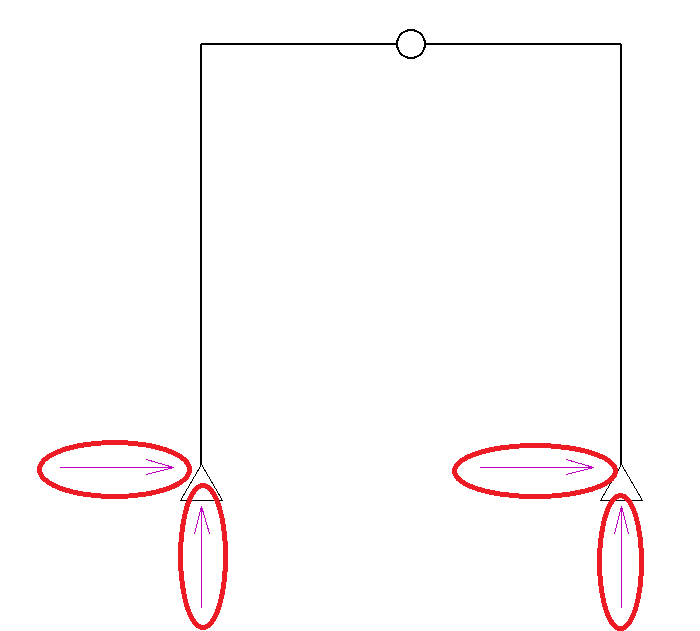
・まず反力数が通常時より1個増えます。
単純梁系ラーメンの時は反力数が3つ、
片持梁系ラーメンの時も反力が3つでしたが、3ピン式のラーメンの場合反力数は4つになります。
・「ピン節点」の場所ではモーメント値は0
すこしイメージが難しいかもしれません。
もしピン節点にモーメント力がかかってしまうなら、「回転が自由な節点」なので回転してしまいます。
もしそうなったらラーメンとしての形状を維持できなくなってしまうことになります。
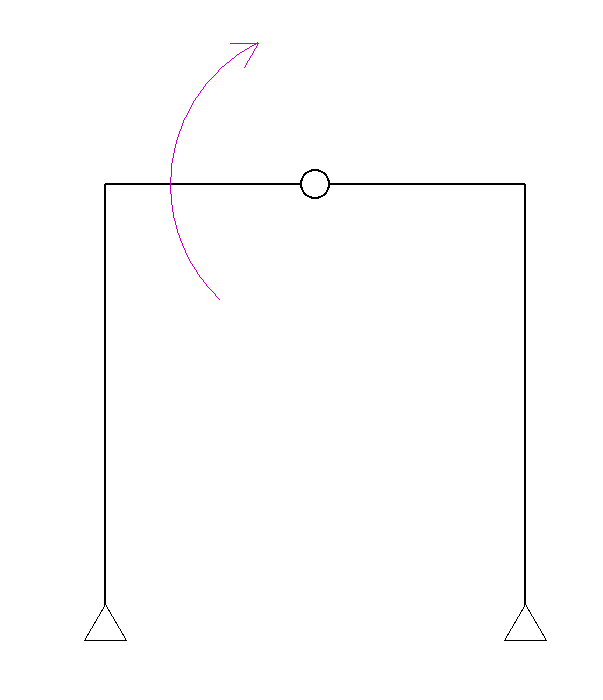
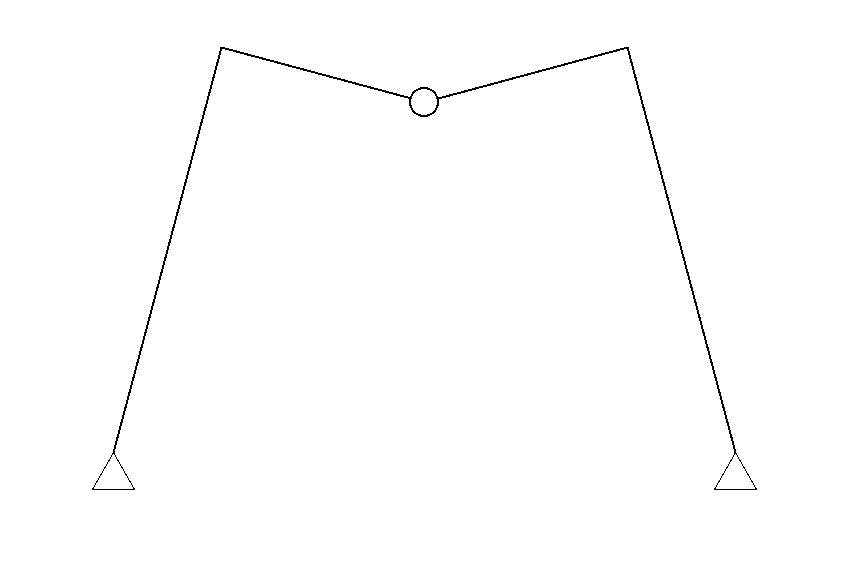
しかし、そうなってしまってはいけません。
つまり、「ピン節点」の場所ではモーメント値を0になるように反力を決めないといけないのです。
・反力を求めるときの条件が増える
これまで反力を求めるときは力の釣合い条件から
ΣX=0
ΣY=0
ΣMo=0
の式に当てはめて求めてきましたが、3ピン式のラーメンの場合これだけでは求めることができません。
先程も考えましたが、
「ピン節点」の地点のM値=0
というのも計算で考慮しないといけません。
つまりまとめると、
ΣX=0
ΣY=0
ΣMo=0
「ピン節点」の地点のM値=0
の連立方程式で解くことができます。
式が多いので面倒くさいと感じるかもしれませんが、実際には複雑な式はあまり出てこないので意外と簡単に解いていくことができます。
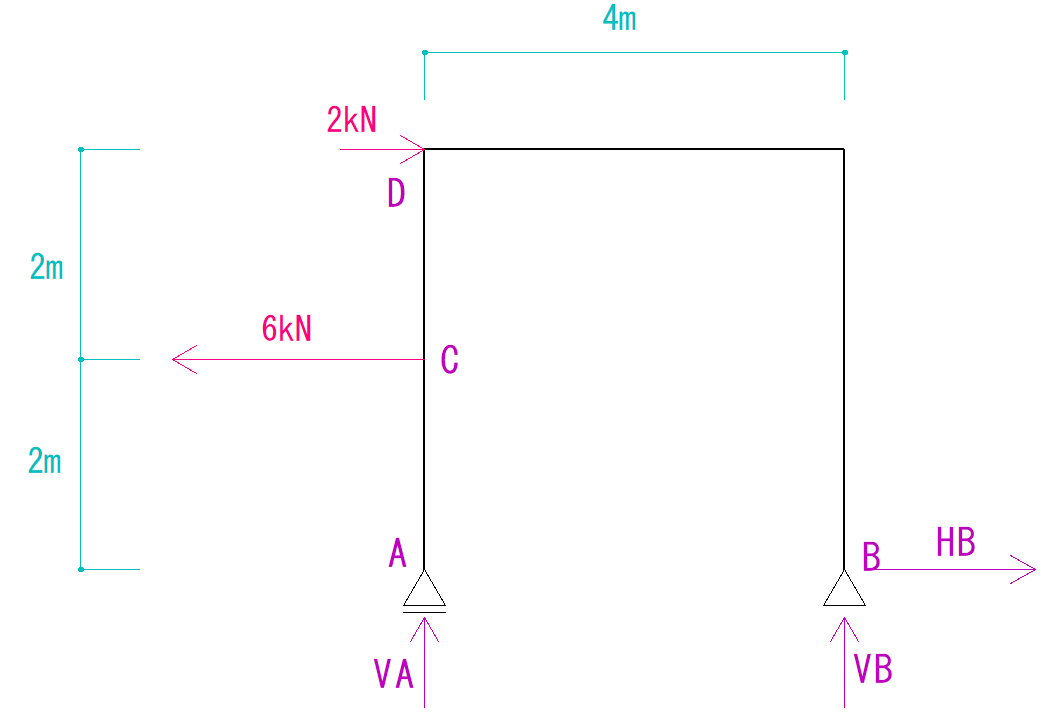
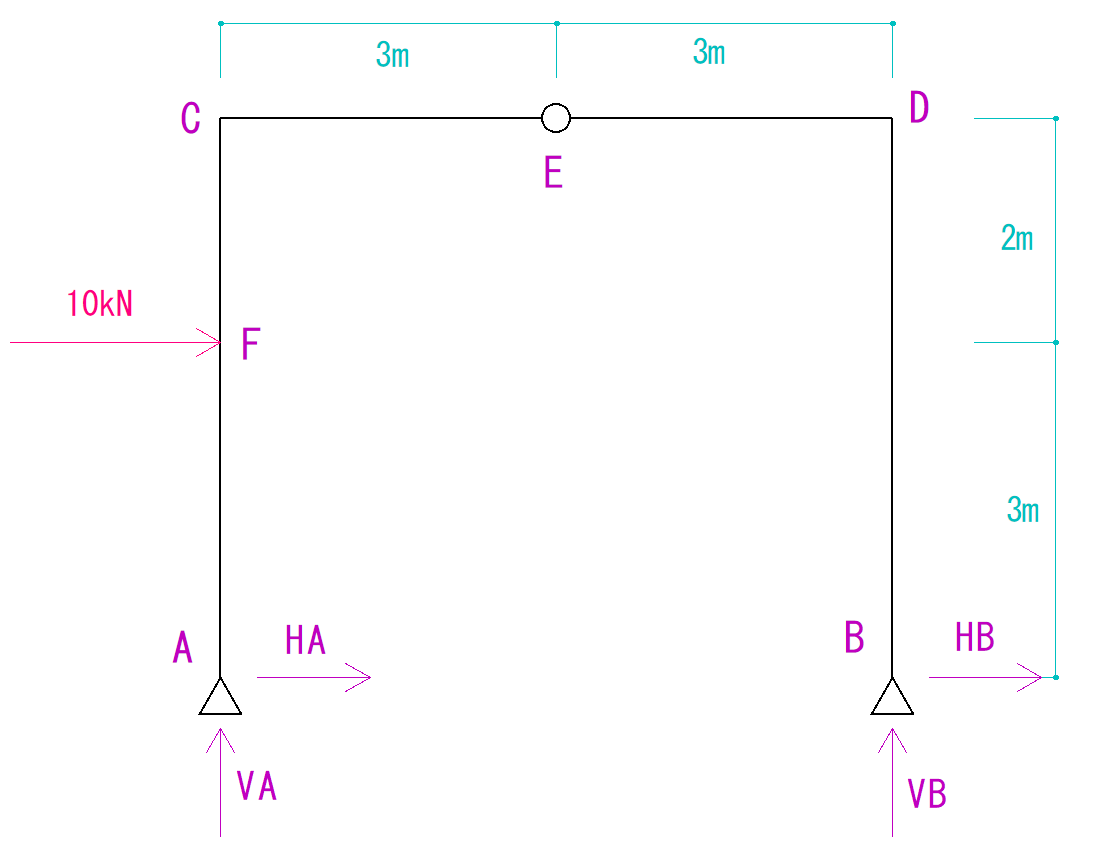
さて次回は例題を使って反力を実際に求めていきたいと思います。