この記事はTwitterから寄せられた質問に答えるものです。
興味ある方は下のリンクの記事をご覧ください。

今回は平行な2力の分解についてしていきたいと思います。
まずは問題を確認してみましょう。
問題
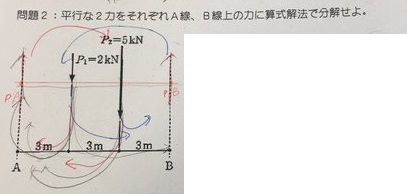
この写真から図を作りました。
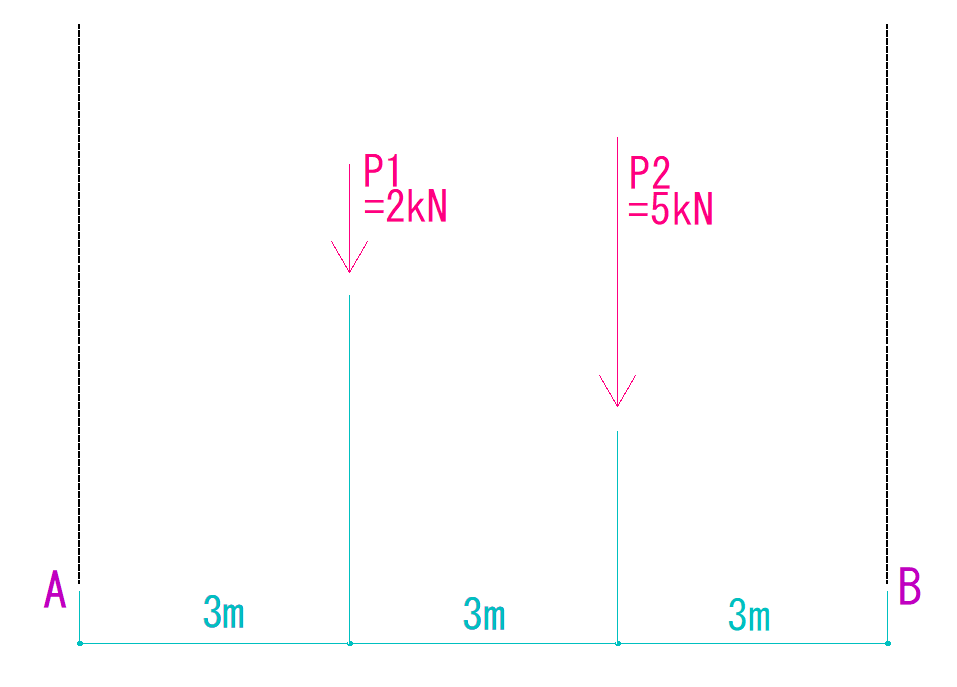
解説
この問題はバリニオンの定理を使って解くことができます。
バリニオンの定理については下のリンクの記事で詳しく解説しているのでそちらをご覧ください。
上の記事での解説では、1つの力を平行な2力に分解する方法を解説していましたが、今回は2つの力です。
どうやって解くのか、詳しく解説していきたいと思います。
手順① ΣMAを求める。
バリニオンの定理によると、ある力を分解するとき、分解した分力と、元の力の任意地点を回す力は等しい、ということが分かります。
言葉ではなかなか伝わらないと思うので、図で確認してみましょう。
PBを下向きと仮定し、任意地点(O点)をA線上に仮定します。
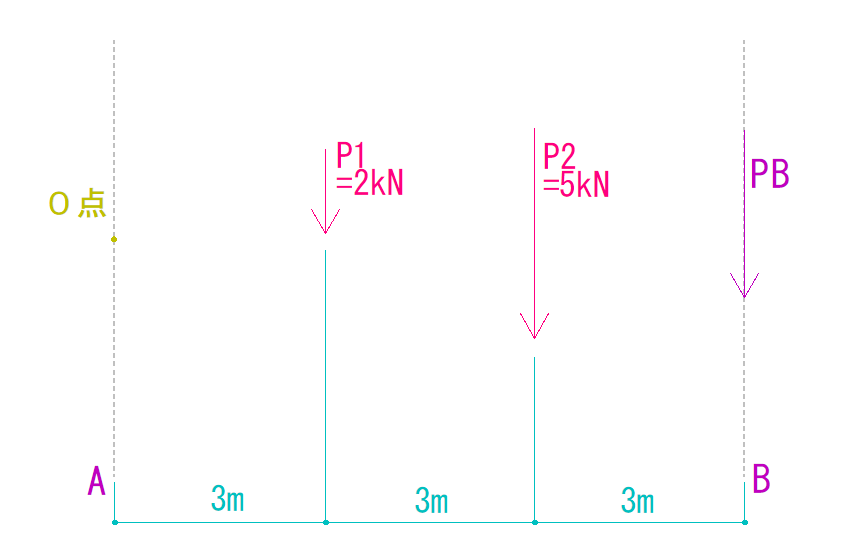
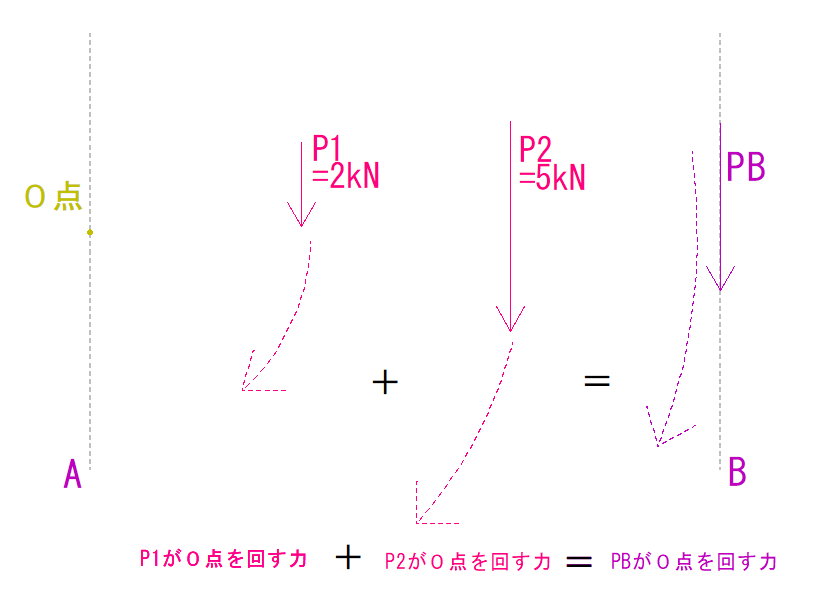
上の図を見て式を立ててみましょう。
まずP1がO点を回す力
2kN × 3m = 6kN・m
P2がO点を回す力
5kN × 6m = 30kN・m
PBがO点を回す力
PB × 9m = (PB×9)kN・m
PAがO点を回す力
PA ×0m = 0
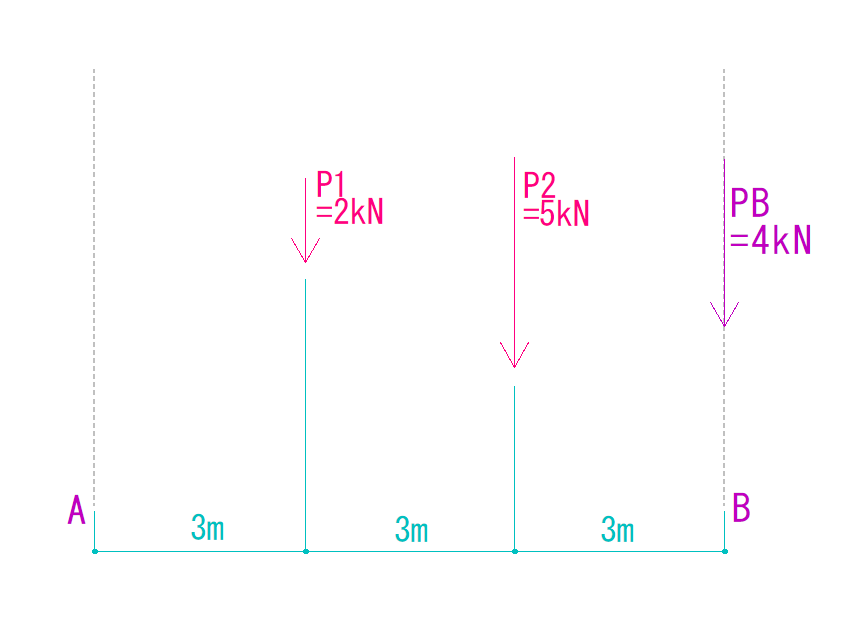
手順② バリニオンの定理に当てはめる
今ほど作った式をバリニオンの定理に当てはめます。
[元の力が任意地点を回す力]=[分力が任意地点を回す力]より
6kN・m + 30 kN・m = (PB×9) kN・m +0
36 = 9PB
PB = 4 kN(仮定通り下向き)
となります。
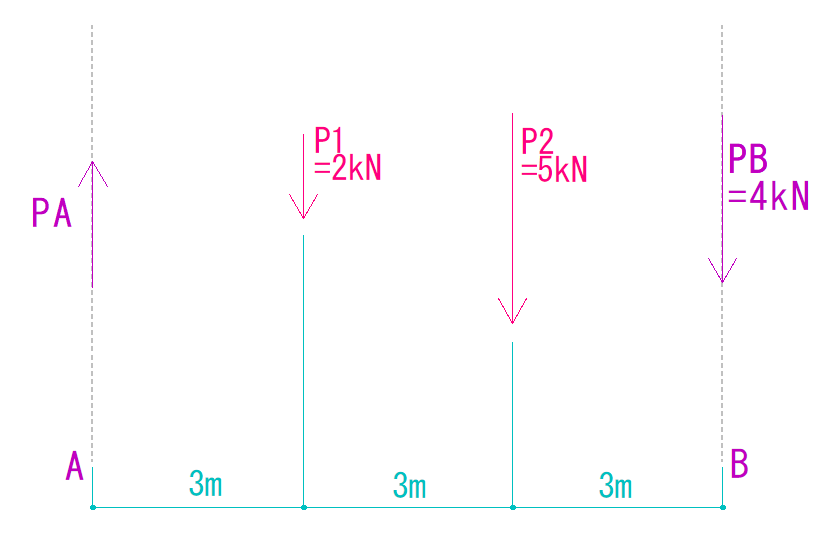
手順③ PAを求める
後は簡単です。
下向きに2kN,5kNがかかっていたので、合計7kNがかかっていることになります。
PBでは4kNを負担しているので、残りの分をPAに負担してもらいます。
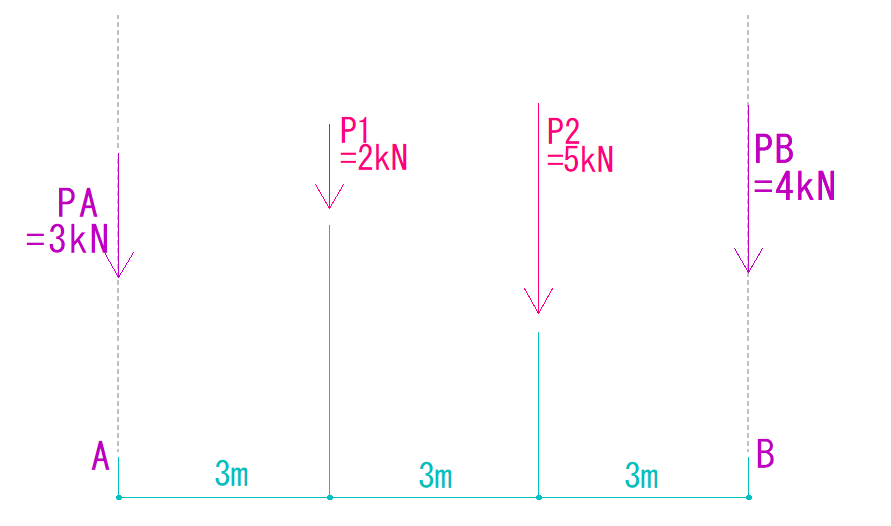
式で書くと、
(-2kN) + (―5kN) = (―4kN) + PA
PA = ―3kN(マイナスが付いているので仮定とは逆の下向き)
となります。
解答
PB = 4 kN(下向き)
PA = 3 kN(下向き)
となります。
まとめ
分野が進んでいくと同じような問題が多く出ます。
「釣合う力」を求めるのか、
「分解」するのか、
しっかりと問題文を見てみましょう。
「釣合う力」を求める場合は、元の力とは逆向きの力になりますし、
「分解」の場合は、元の力と同じ向きになります。
送っていただいた問題に、書かれていた式はあっていましたが、符号ミス、もしくは考え方のミス(釣合いと分解を混同してしまっていた(?))ように見受けられました。
式があっていたので、考え方はあっていたのかと思います。
テストではケアレスミスによって点を落とさないように気を付けましょう。