今回は単純梁の反力を求めるシリーズの第4弾です。
単純梁に等変分布荷重がかかった場合の反力の求め方を考えていきましょう。
まず、このような問題を解くにあたり、等変分布荷重が何なのかを理解する必要があります。
この記事でも少し触れますが、詳しくは下のリンクの記事をご覧ください。
例題
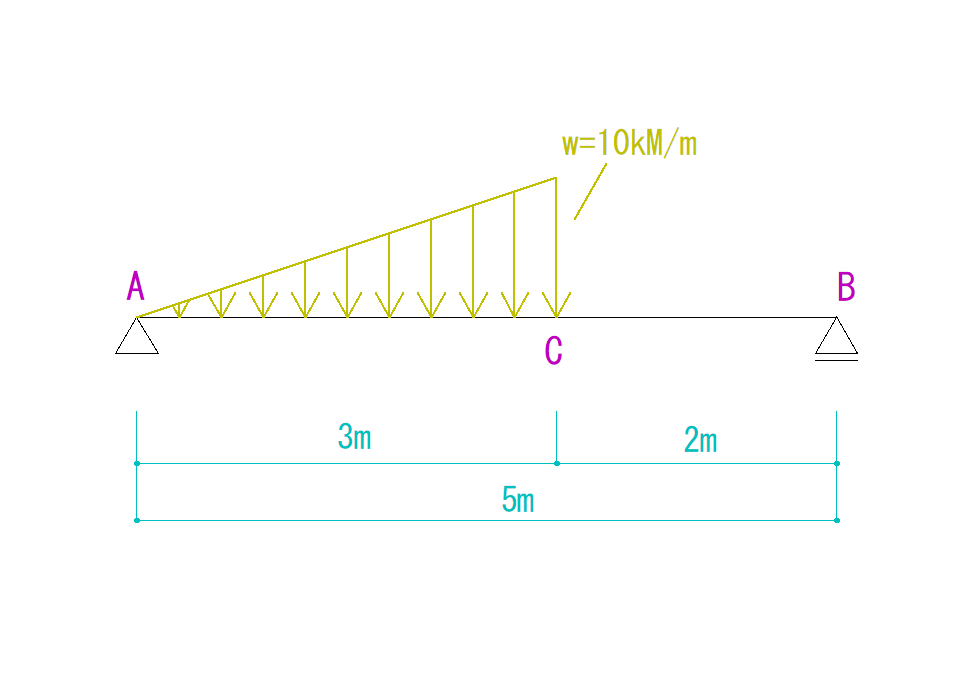
下の図を見てそれぞれの反力を求めなさい。
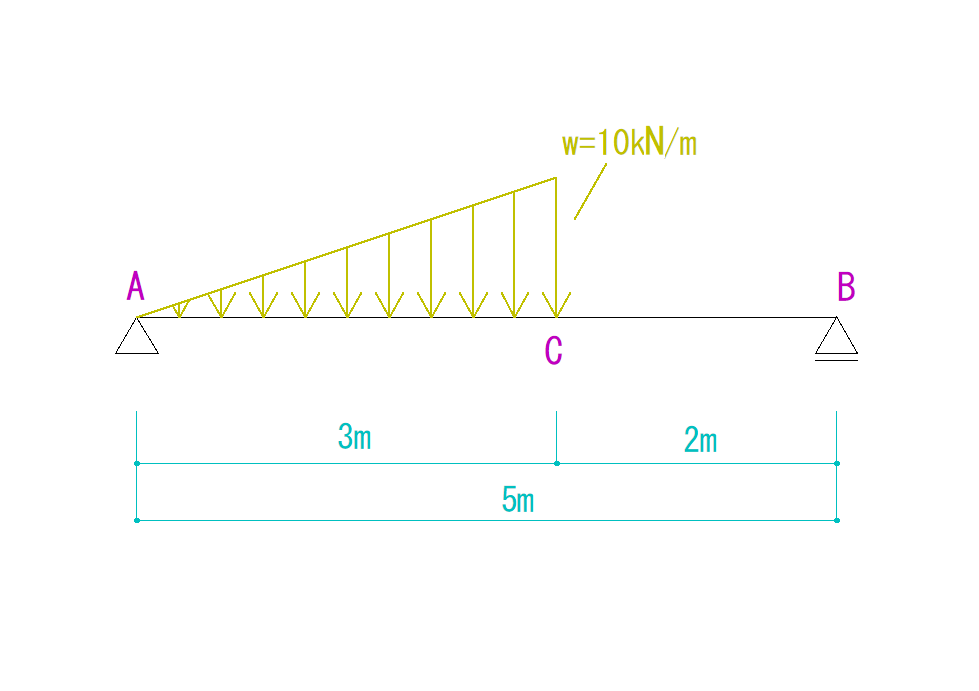
解説
反力の仮定
まず、それぞれの支点にどの種類の反力が、いくつかかるかを確認します。
これについては下のリンクの記事を参照ください。
この場合は下のように反力を仮定することができます。
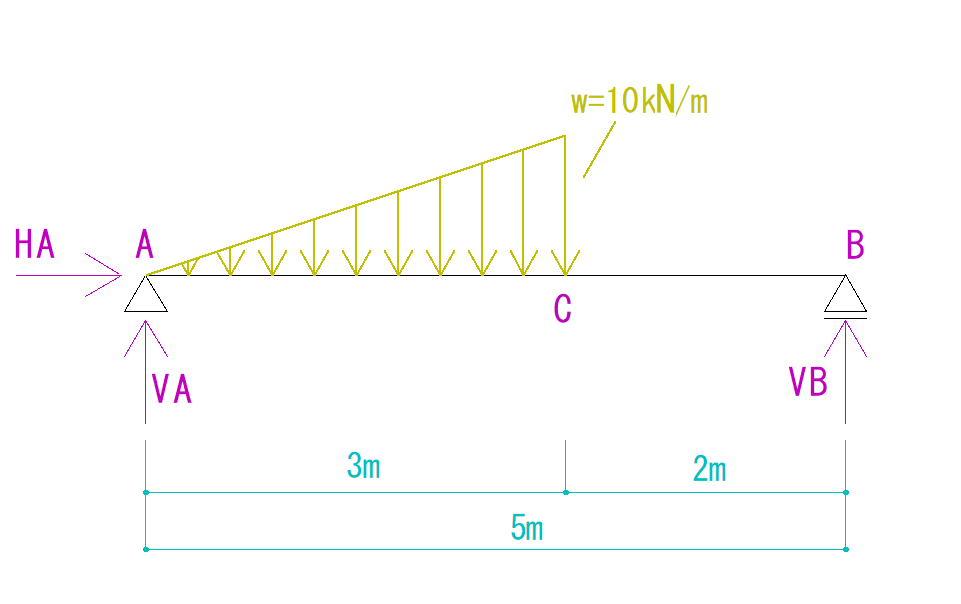
注意ですが、この時、反力の符号がプラス向きにするようにすることをおすすめします。
補足:力の符号について
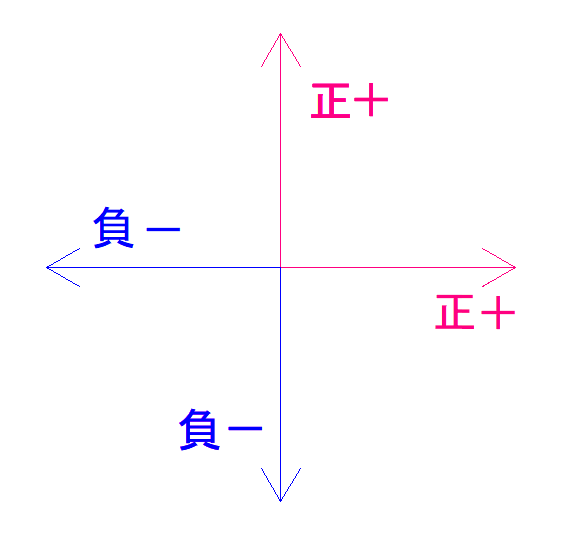
そうすると、これから式を立てるとき符号ミスが減ります。
(明らかにマイナスの向きにかかる場合は、仮定でマイナス向きにしてもいいですが、符号は間違えないようにしましょう。)
では、問題を解いていきます。
解き方
等変分布荷重の合力の大きさ
等変分布荷重のままでは計算しづらいので、この等変分布荷重の合力を求めてあげます。
以前の記事でもやりましたが、等変分布荷重の合力は面積の公式で求めます。
等変分布荷重の合力の公式は
等変分布荷重がかかっているところの距離[l]×等変分布荷重の最大厚さ[w] ÷2
となっています。

言い換えれば等変分布荷重の底辺×高さ÷2とも言えます。
今回の場合は
等変分布荷重がかかっているところの長さ[l]=3m
等変分布荷重の最大厚さ[w]=10kN/m
となっているので、それを計算すると…
3m × 5kN/m ÷ 2= 15kNとなります。
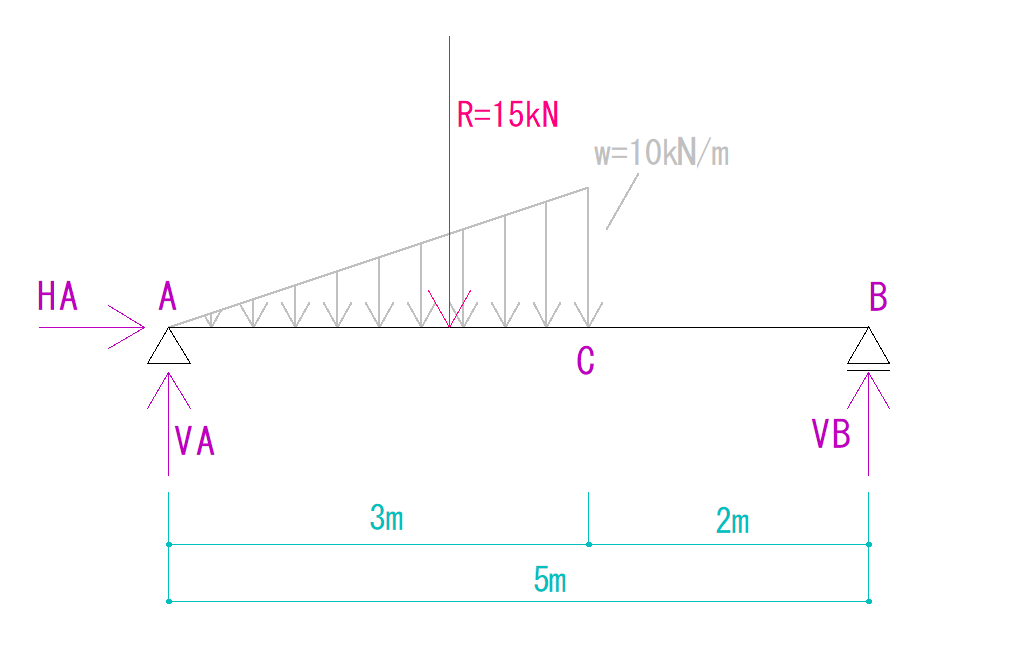
等変分布荷重の合力のかかる場所
先程求めたように、等変分布荷重の大きさは面積を求める形で計算することができました。
では、その合力はどこにかかるのでしょうか?
それは
等変分布荷重の重心地点
です。
重心と出ていますが、難しい計算は必要ありません。
直角三角形の重心は鋭角から2:1に分けたところになるからです。

今回の場合はA点から右に1mの場所になるとわかります。
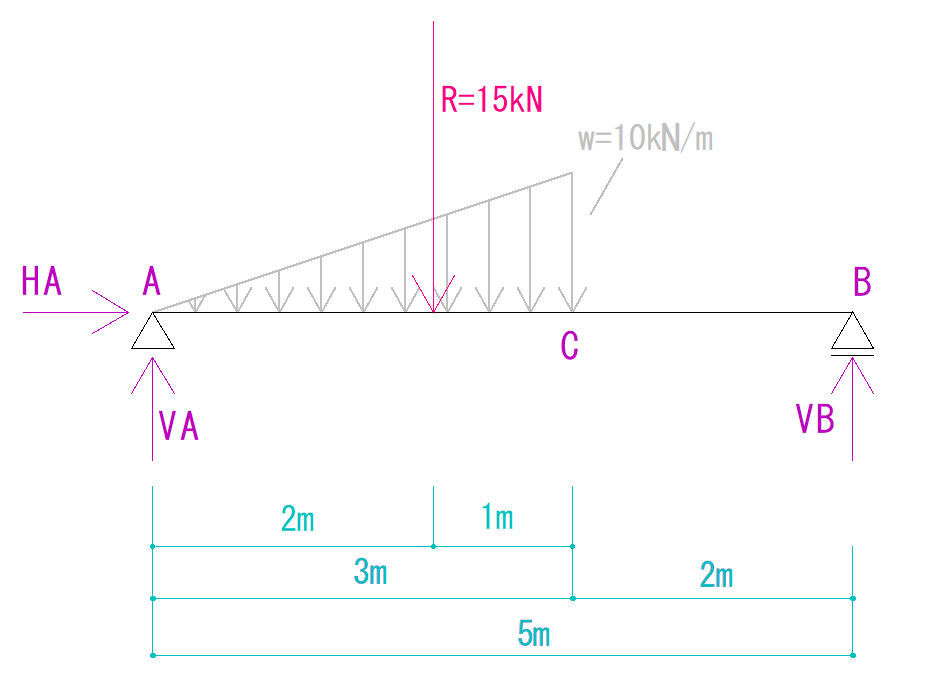
反力の求め方
ここまでくれば、後は単純梁に集中荷重がかかった場合の解き方と同様です。
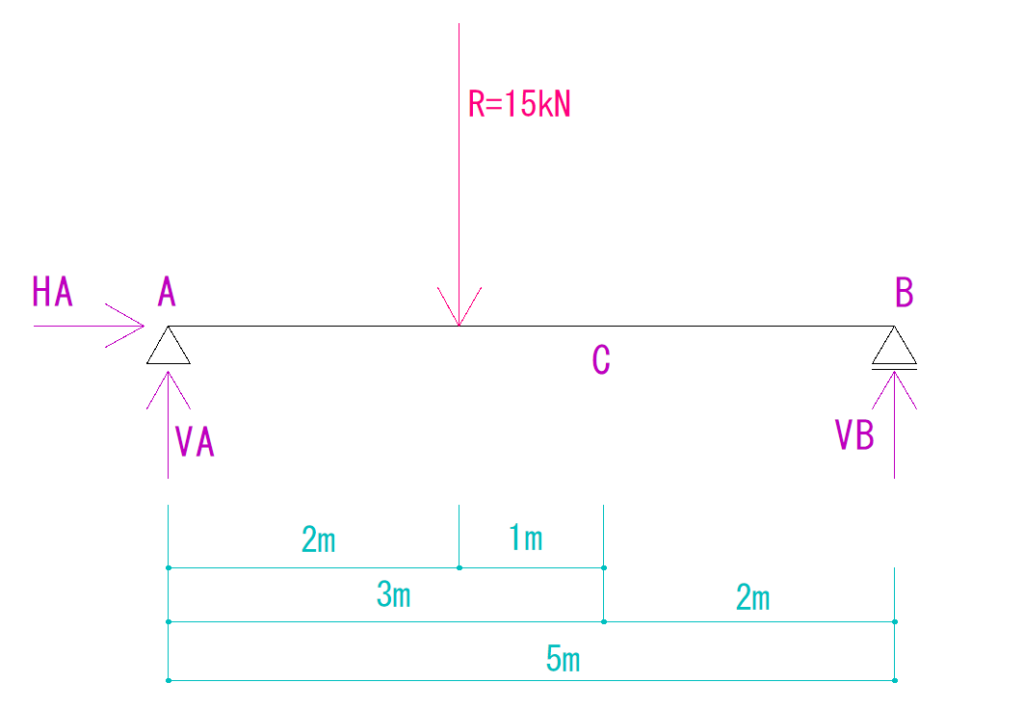
詳しく知りたい方は下のリンクの記事をご覧ください。
計算内容は下記のとおりです。
水平反力がかかっていないためHAは省略
ΣRM=0より、
A点をO点(基点)とし、RMO(それぞれの力がO点を回す力の合計)を求めます。
VA × 0m + 15kN(等変分布荷重の合力) × 2m +(- VB × 5m) = 0
【VBの仮定の向きだとO点を反時計回りに回すのでマイナスを付けます】
30kN・m + (-5VB kN・m) = 0
30 kN・m =5VB kN・m
VB = 6kN (仮定通り上向き)
ΣY=0より、
VA + (-15kN) + 6kN = 0
VA = 9kN (仮定通り上向き)
答え
HA=0
VA=9kN(上向き)
VB=6kN(上向き)
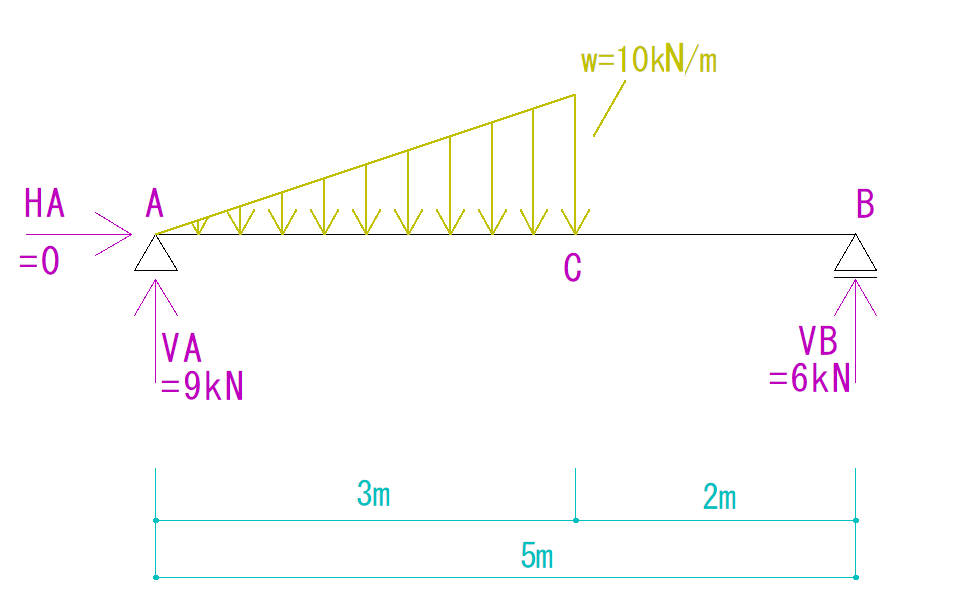
となります。