今回からは梁の種類が変わり、片持梁の場合のQ(せん断力)図M(曲げモーメント)図を描いていきます。
それにあたり、片持梁とはどういうものか理解する必要があります。
よくわからない方は、下のリンクの記事をご覧ください。
ではまず、集中荷重がかかった場合の描き方を解説していきたいと思います。
例題
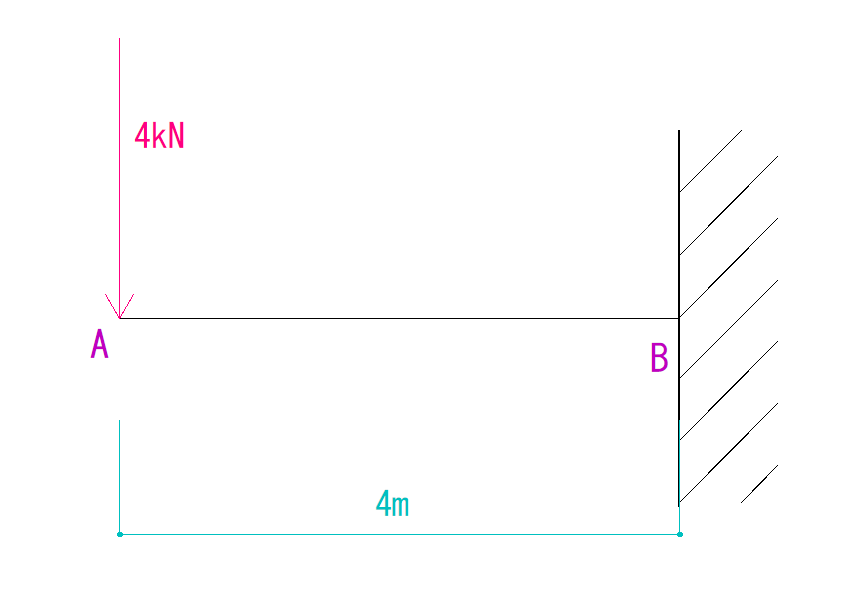
下の図を見てQ図M図を求めなさい。
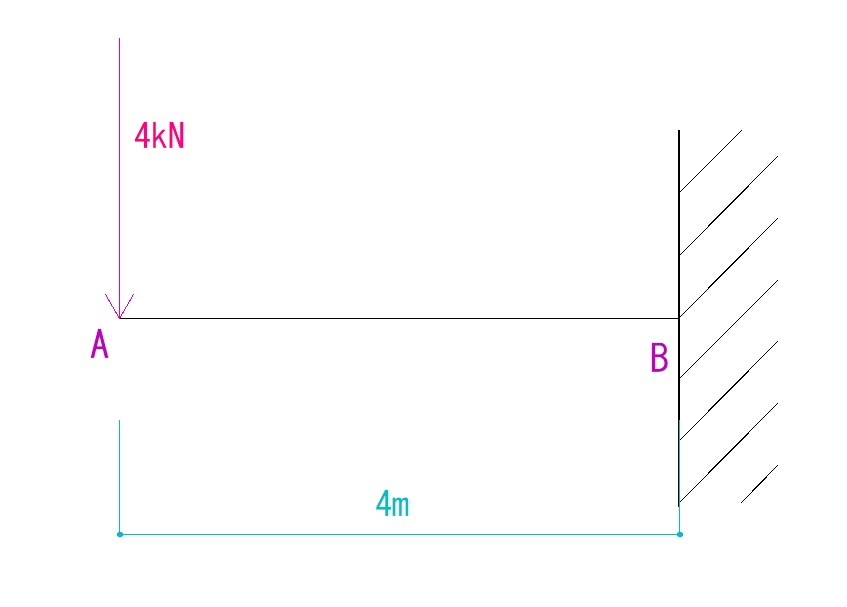
解説
反力の仮定
まずは反力を仮定し求めていきます。
片持梁の場合、反力がかかるのは片方の支点だけです。
しかも今回はこれまでやった支点とは違う種類のものです。
そこで最初は、反力の数と種類を確認します。
詳しくは下のリンクの記事をご覧ください。
簡単に固定端の表を出しておきます。
固定支点(固定端)

・水平移動=しない
・垂直移動=しない
・回転 =しない
支えられる反力は3方向
これを見るとわかる通り、固定端はこれまでの水平力(引張力)、垂直力(せん断力)のほかにモーメント力の反力も出ることが分かります。
つまり反力は下の図のようになるということです。
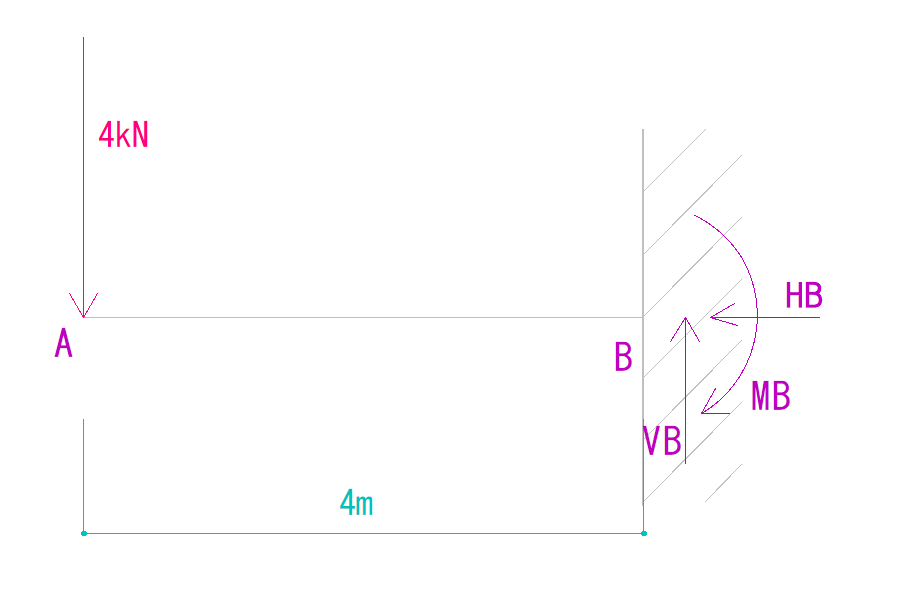
では一つずつ考えていきましょう。
水平力(引張力)
今回の場合は、集中荷重が垂直にかかっており水平方向への荷重は生じていません。
つまり今回も水平反力及びN図も省略することができるとわかります。
垂直力(せん断力)
これは見てわかる通り、上からかかっている力と同等の力を下から加える必要があります。
式で書くとこうなります。
ΣY=0より
-4kN+VB=0
VB=4kN(仮定通り上向き)
モーメント力
まずは、荷重がB点にかけているモーメント力を求めましょう。
モーメント力について復習したい方は下のリンクの記事をご覧ください。
モーメント力の公式より
4kN × 4m = 16kN・m
反時計回りの為、負の符号をつけて
-16kN・m
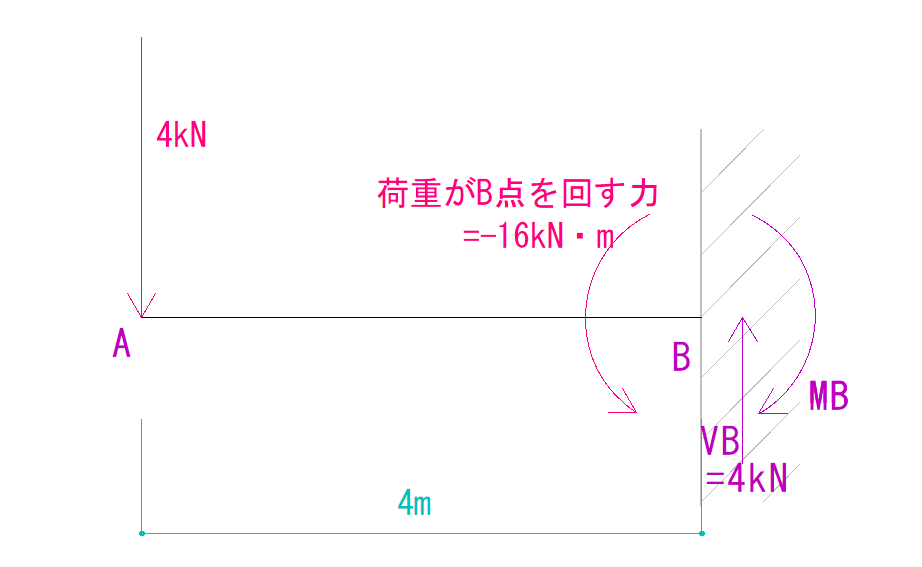
となります。
そこから反力を求めると、
ΣMB=0より
-16kN・m + MB = 0
MB = 16kN・m(仮定通り時計回り)
となります。
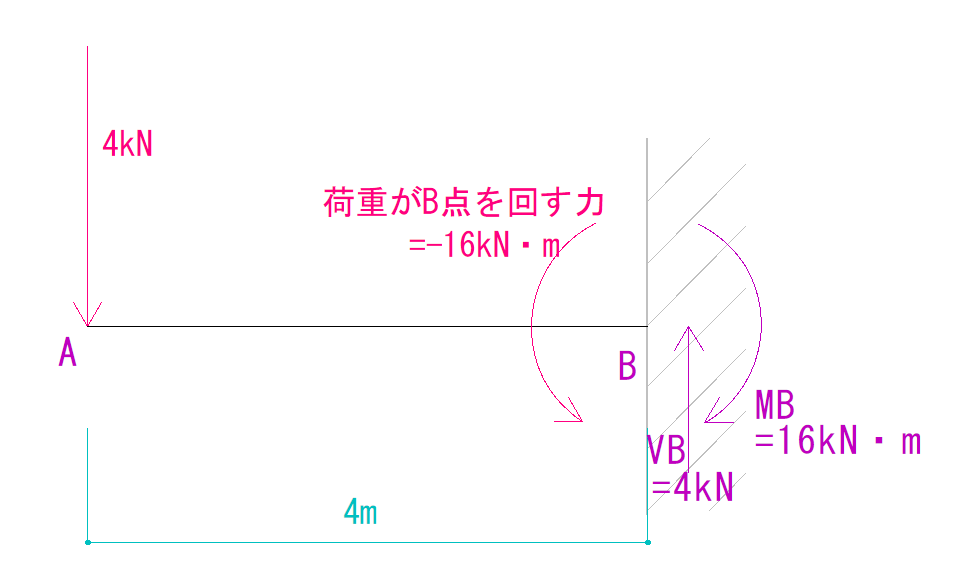
Q図の描き方
描き方はこれまでと同じです。
まず垂直方向の力だけを見てみましょう。
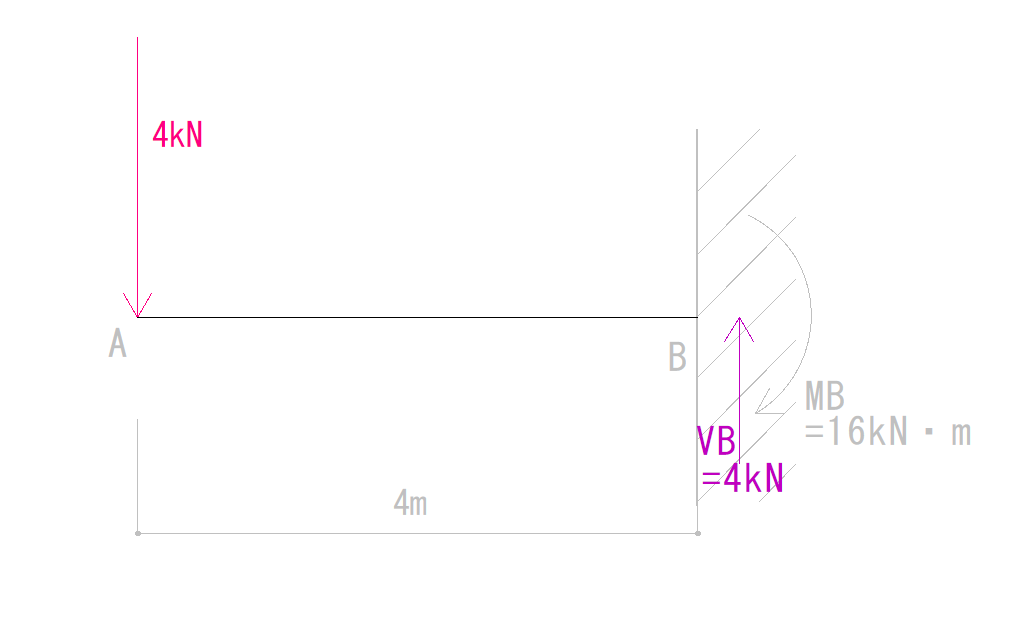
左から(右からでも可)見ていきます。
まず、A点で上からの荷重がかかっています。
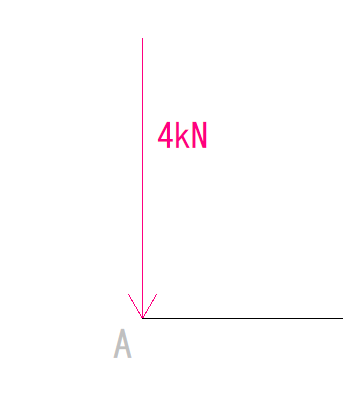
部材の左側に下向きの力がかかった場合、符号は+と-どちらでしょうか?
下の表から確認してみます。
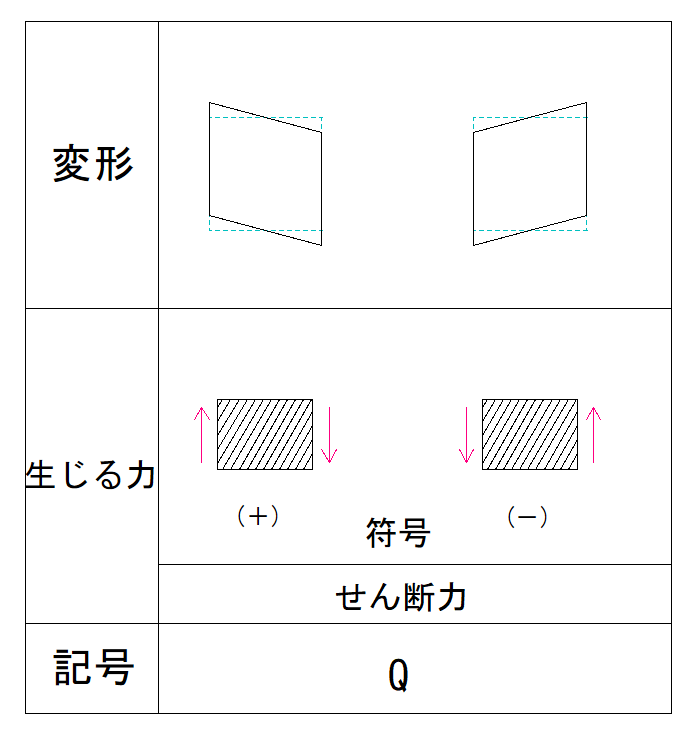
左側に下向きの力がかかった場合、符号は-でした。
なので、Q図には―4kNと描きこみます。

次に力がかかっているのはB点です。
先程と同じように考えると、B点でも-4kNと書き込めばいいことが分かります。
そうするとQ図は直線形(長方形型)になりました。

最後に符号と大きさを書き入れて完成です。
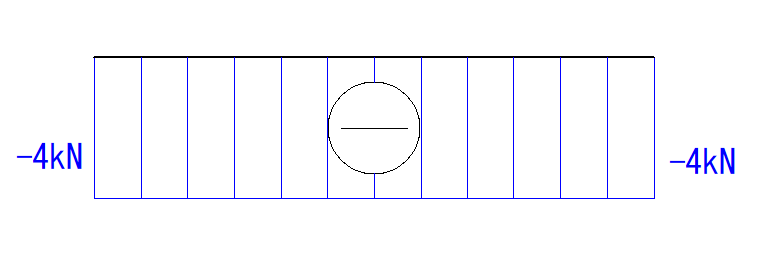
M図の描き方
M図のやり方はこれまでと少し違うかもしれません。
というのも、これまでの支点はモーメント反力を持たなかったため、両端は必ず0になっていました。
しかし今回はモーメント反力があります。
そのため、固定端の方はモーメント力が0とは限りません。
しかしそれ以外はやり方も考え方も同じです。
モーメントの値は力がかかるところで変化しますが、形は直線形(三角形型)になります。
今回も左から(右からでも可)見ていきましょう。
まずA点を見ます。
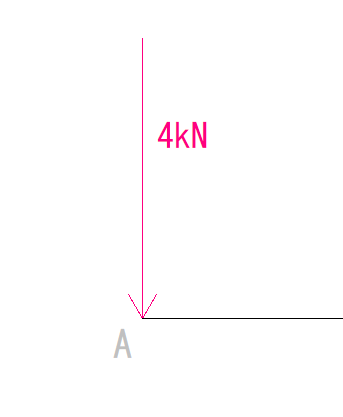
ここは支点すらないので、モーメント値も0です。
次にB点です。
B点のモーメント値は、すでに求めてあります。
MBの値です。
そのため大きさはMB = 16kN・mとなります。
符号ですが、今回はどちらでしょうか?
下の表を見て確認しましょう。
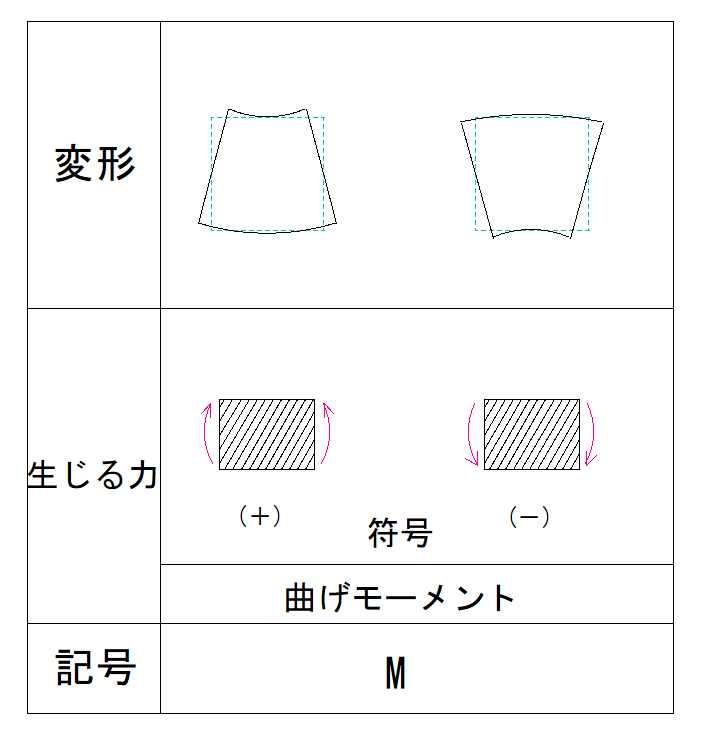
上向きに出っ張るイメージなので符号はーになります。
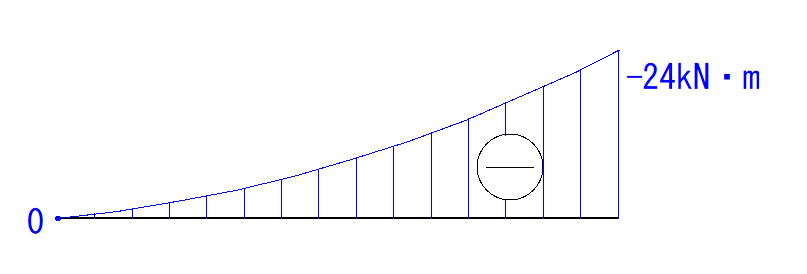
よって、B点のモーメント値は-16kN・mとなります。
最後に点を結んで符号を書き、最大値をかきいれれば完成です。
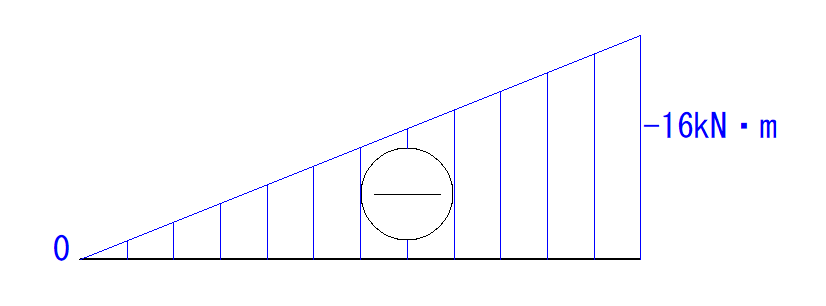
注意点 モーメント力の符号とM図の符号について
問題で出てきたのですが、解いていてこんがらがりやすい部分を少し解説したいと思います。
実は今回の問題ですが、B点にで少し複雑なことが起きていました。
それは、
MBの値とM図の値は一緒なのに符号が逆!
ということです。
MBは+でしたがM値は-になっていました。
なんでそんなことが起きたのでしょうか?
それはずばり…
MBの値とM図の値は別物だから
です。
確かに同じモーメントについての物なのでごちゃごちゃしてしまいますが、モーメント力とM図の値は別物です。
もう少し詳しく言うと、モーメント力の符号は力単体の符号になります。
しかしM図の値は、部材全体がどういう風に変形しようとしているかの符号になります。
なので、ここを混同してごちゃごちゃにならないように気を付けましょう!
(筆者はここでごちゃごちゃになってしまった記憶があります…)