さて今回からはラーメン構造の分野について考えていきたいと思います。
実は以前に一度ラーメン構造についての記事を書いていたのですが、新たにラーメン構造の分野に入るということで、今回改めて、ラーメン構造について解説していきます。
以前の記事をご覧になりたい方は下のリンクから見ることができます。
では早速解説していきたいと思います。
ラーメン構造とは?
ラーメン構造…と最初出てきたとき何か思い浮かべませんでしたか?
…ちなみに私はラーメンを食べたくなりました。

もちろんラーメン構造のラーメンとは、食べるラーメンではありません。
調べたところ、ドイツ語からきているようです。
さて、ラーメン構造とはどういう構造なのかを簡単に理解しましょう。
Wikipedia先生には、こう書いてありました。
ラーメン (独: Rahmen) とは構造形式のひとつで、長方形に組まれた骨組み(部材)の各接合箇所を剛接合したものをいう。ドイツ語で「額縁」の意。建築・土木構造の分野では柱が梁と剛接合している構造をラーメン構造という。
Wikipedia 「ラーメン(骨組)」
…建築を勉強している方ならなんとなく内容は理解できるでしょうか?
ラーメン構造とは簡単に説明するのであれば、「柱と梁」といった二つの部材がとても頑丈につけられている構造物のことです。
この”とても頑丈に”というのは、木で組んだとか、そういうものではありません。
溶接して、どうやっても分離させるのが難しいものです。
例としてS造(鉄骨構造)のようなものがあげられます。

ラーメン構造の場合、やはり構造設計も変わってきます。
柱と梁の部分を継ぎ目とせずに一体の物として計算します。
しっかりと理解しておきましょう。
ラーメン構造の種類
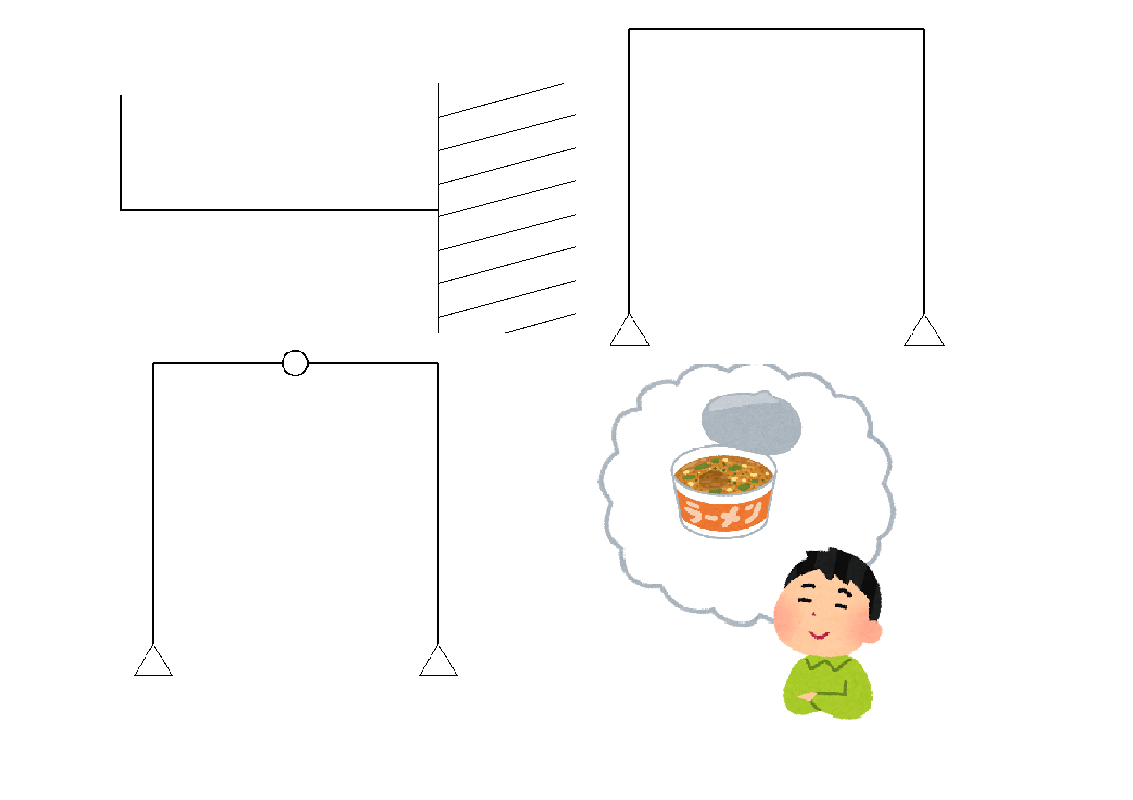
ラーメン構造には種類が3つあります。
以下の通りです。
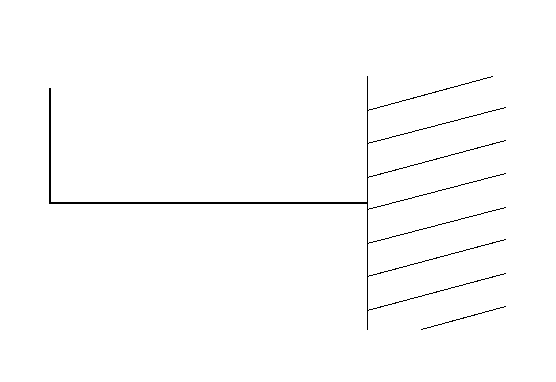
片持梁系ラーメン
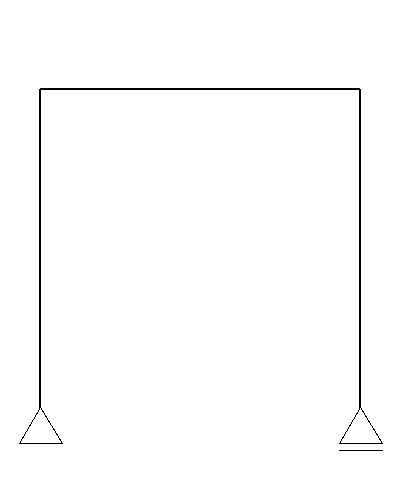
単純梁系ラーメン
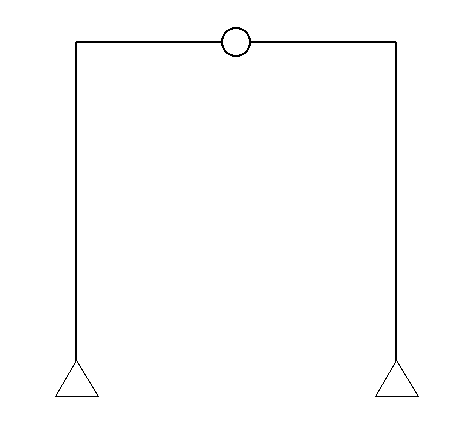
3ピン式のラーメン
それぞれの特徴を考えていきましょう。
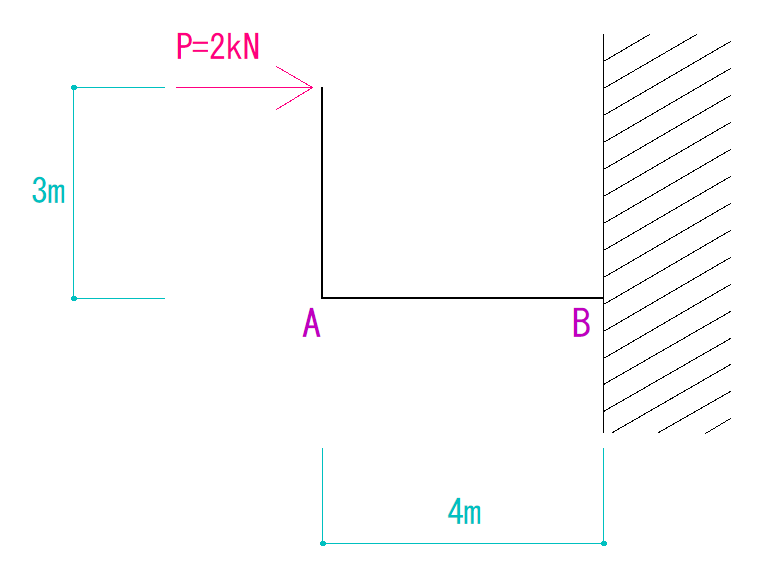
片持梁系ラーメン

これはぱっと見、片持梁のような形をしていますが、張り出しているところが折れ曲がっているのでラーメン構造として分類されます。
別記事で詳しく解説しますが、反力はこれまで通りのやり方で出すことができます。
曲者はN図Q図M図です。
描く場合の符号に気を付けてください。
下の図のようになります。
N図Q図の場合
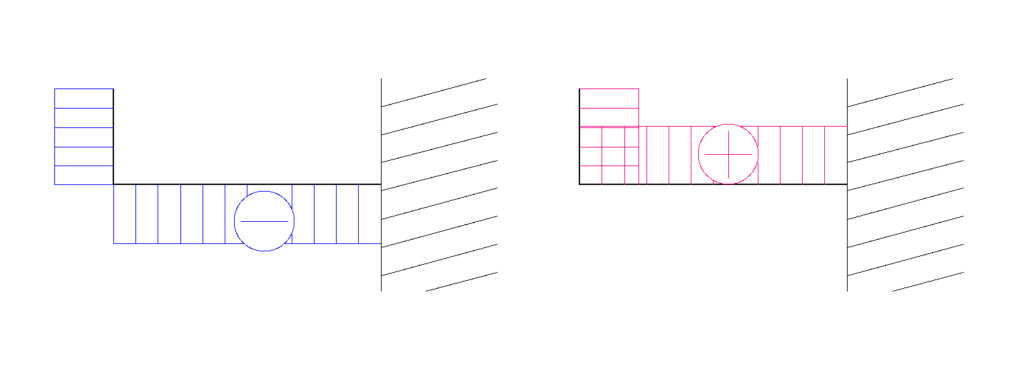
M図の場合
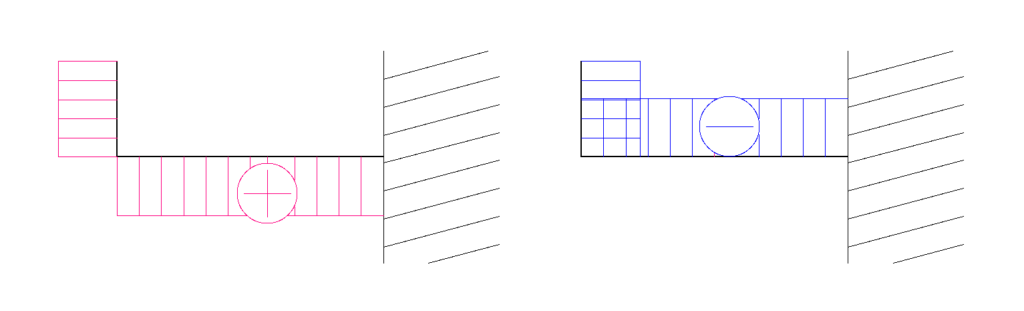
イメージとしては、水平な部材を基準として一直線に伸ばしたときの符号の位置が折れ曲がっている、という感じです。
言葉ではうまく伝わらないかと思いますので、これについても図をご覧ください。
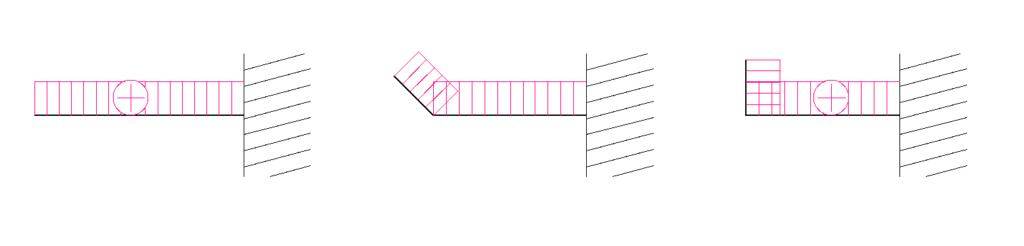
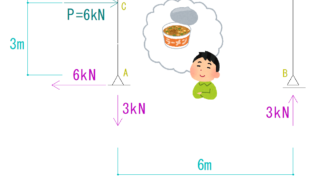
単純梁系ラーメン

「Theラーメン構造」という形をしています。
構造設計の問題でラーメン構造というと、基本的にこの形のものを指しますのでよく覚えておきましょう。
これも別記事で詳しく解説しますが、反力はこれまで通りのやり方で出すことができます。
やはり曲者はN図Q図M図です。
描く場合の符号に気を付けてください。
下の図のようになります。
N図Q図の場合
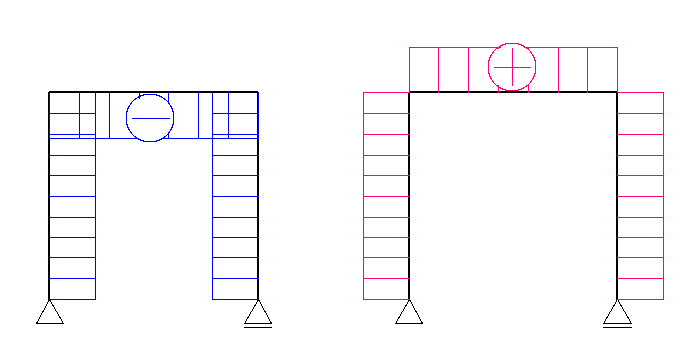
M図の場合
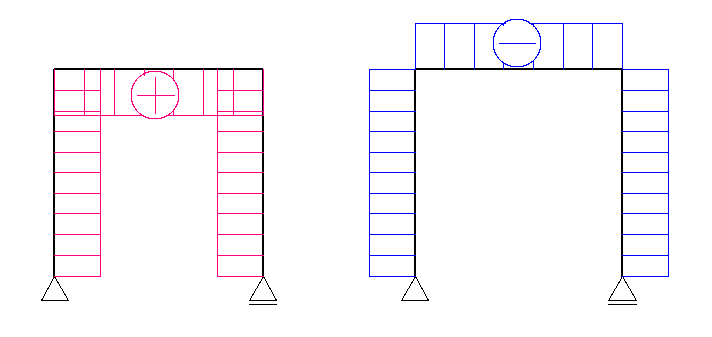
イメージとしては、水平な部材を基準として一直線に伸ばしたときの符号の位置が折れ曲がっている、という感じです。
言葉ではうまく伝わらないかと思いますので、これについても図をご覧ください。
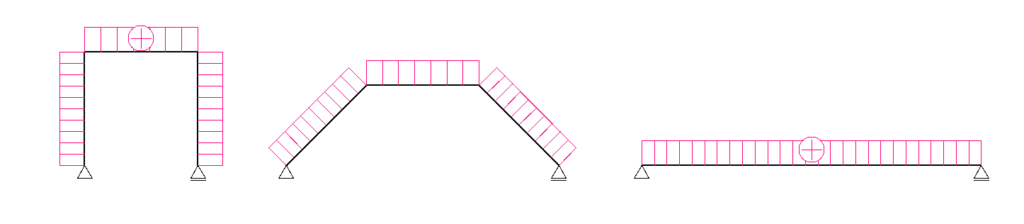
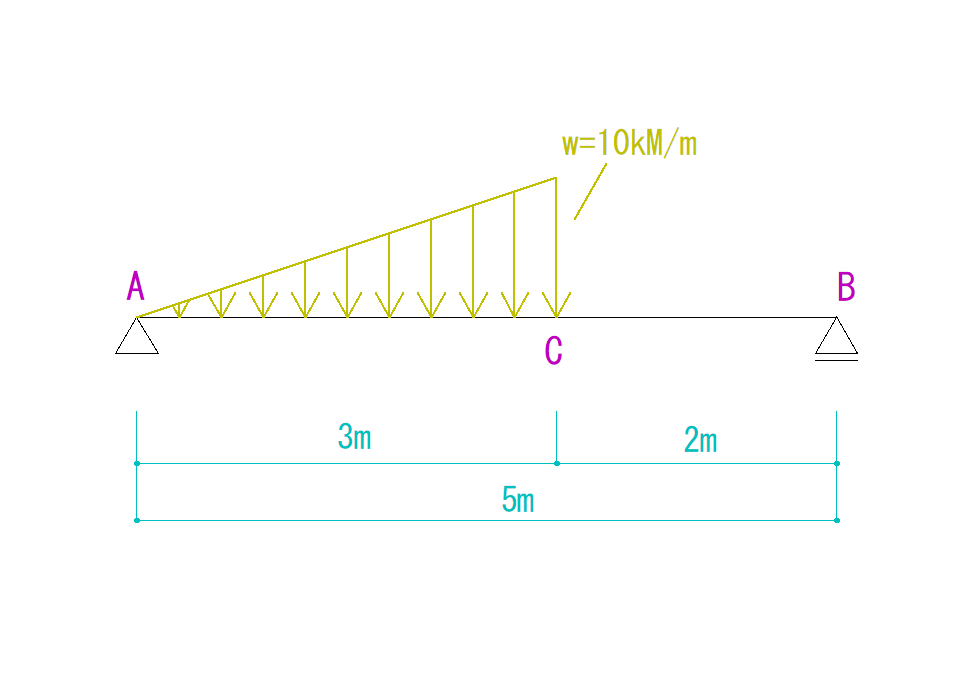
3ピン式のラーメン

これも見た感じ「単純梁系ラーメン」に見えるかもしれませんが、全くの別物です。
まず真ん中に「ピン節点」と言われる節点が存在します。(丸になっている部分です)
これは剛接合されていない節点(めちゃめちゃ頑丈に接合していない節点)という意味です。
構造設計上、そのような接合部は「力がかかると回転してしまう」ということで計算します。
…いやいや、建築物で回転してしまう節点なんて危なくてしょうがないじゃないか!
と思われたでしょうか?
もちろん、ちょっとやそっとの力じゃ回りません。
しかし、すごく大きな力がかかった場合に、それに耐える力がなく、回ってしまうという意味です。
これもまた別記事でしっかりと解説しますが、ピン節点の場所ではM値は必ず0になります。
しっかりと覚えておきましょう。
符号については、単純梁系ラーメンと同じ考え方なので省略します。