この記事はTwitterから寄せられた質問に答えるものです。
興味ある方は下のリンクの記事をご覧ください。

トラスの解き方は大きく分けて二種類
「節点法」と「切断法」があります。
また、「節点法」にも図式解法と算式解法があります。
この記事では最初に、「節点法」の図式解法について解説していきたいと思います。
節点法とは?
まず、節点法とはどういう考え方でしょうか?
簡単に言うと、各節点ごとに見ていき、それぞれに釣合う力を求めていく、というものです。
もう少し詳しく説明しましょう。
トラスは、ある条件が満たされています。
それは、各節点での力が釣合っている
というものです。
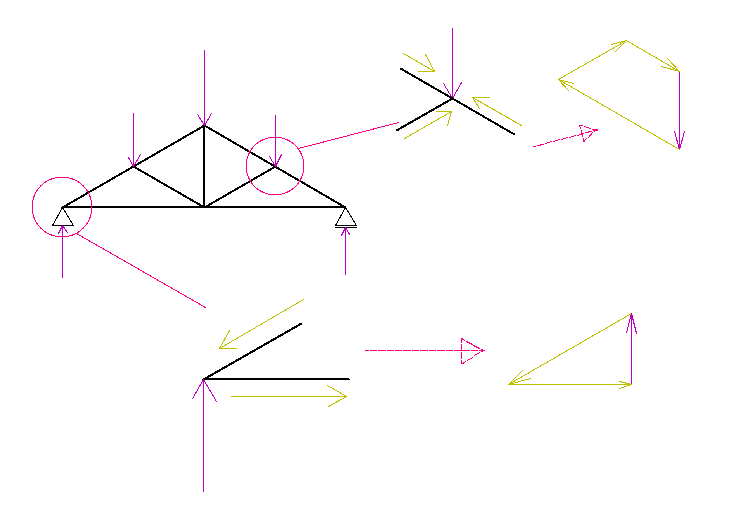
その条件を利用して、一つ一つの節点をそれぞれ考えて解いていくのが節点法です。
例題
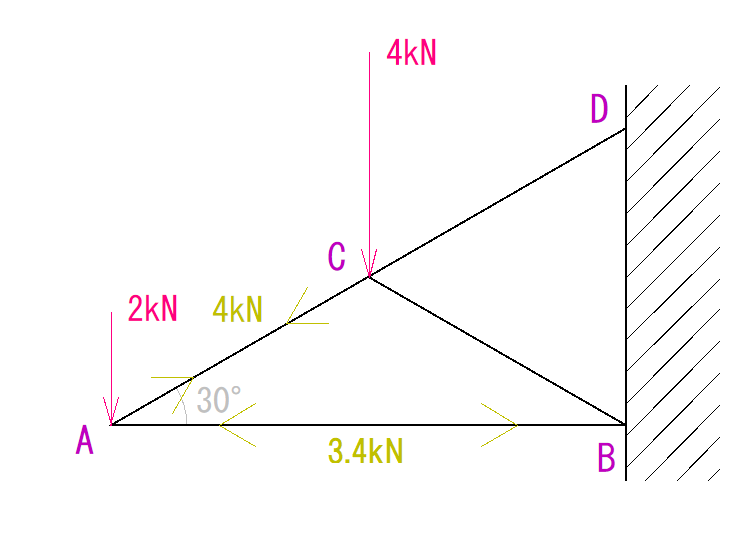
下のトラスを節点法の図式解法で解きなさい。

解説
①A点の示力図を描いて解く
トラスの問題は基本、一番左端から見るのがセオリーとなっています。
なのでA点から考えていきましょう。
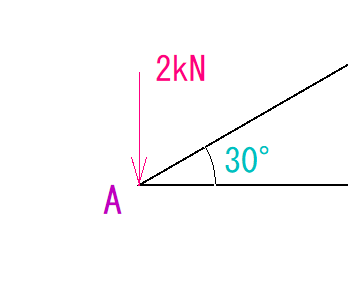
A点には垂直に、荷重2kNがかかっています。
これを、別の用紙に、線の長さを指定して書きましょう。
(例えば1kN,1cmとして書く。)
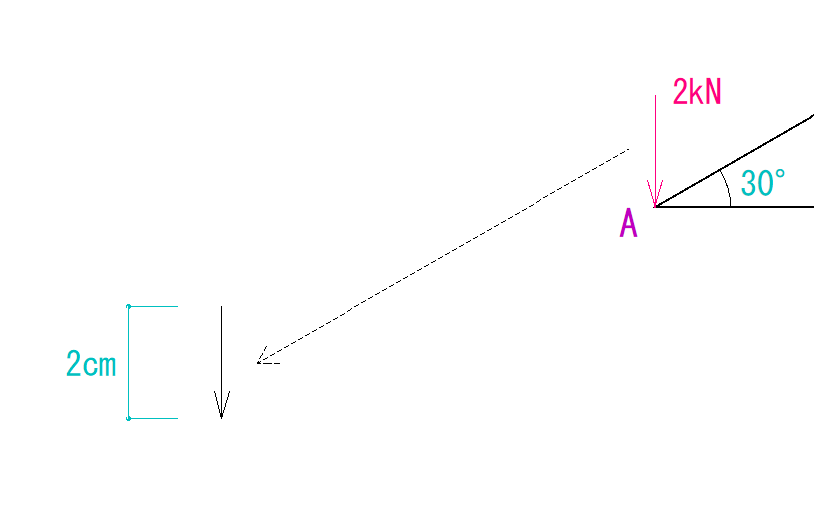
次に、A点に接している部材に目を向けます。
先程書き写した荷重の矢印の先端につながるように、部材の線を平行移動させます。
このときの注意ですが、すでに分かっている部材から時計回りの順番で、平行移動させていきましょう。
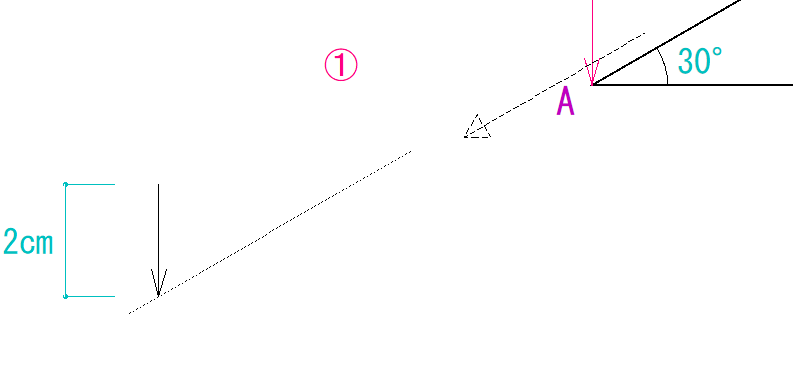
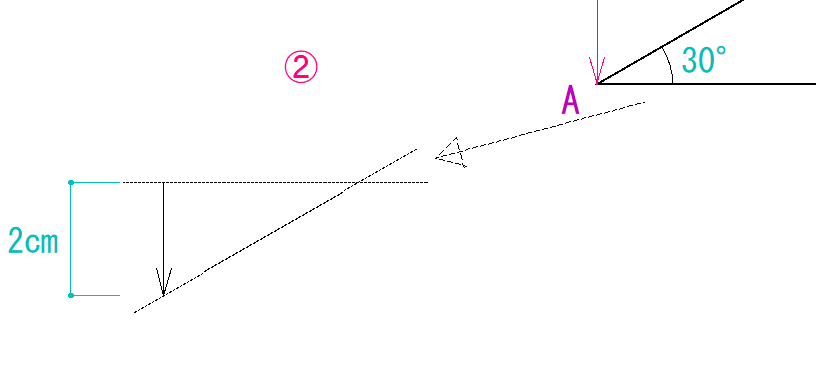
最終的に三角形の形(示力図が閉じる形)になるようにします。
そうしたら、矢印の向きがが一周するように付け、それぞれの辺の長さ定規ではかります。
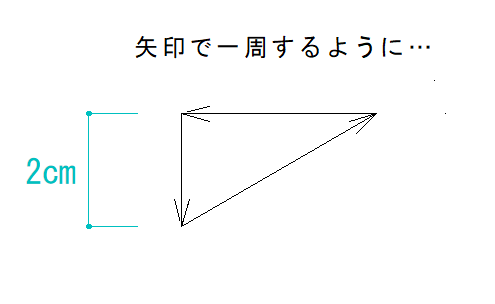
正確にできていれば、下の図の長さになっているはずです。
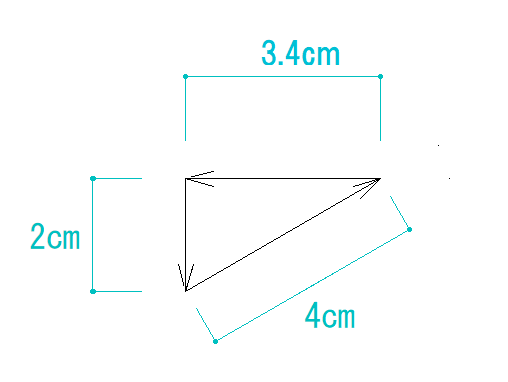
ここから、部材の軸方向力が2つ分かりました。
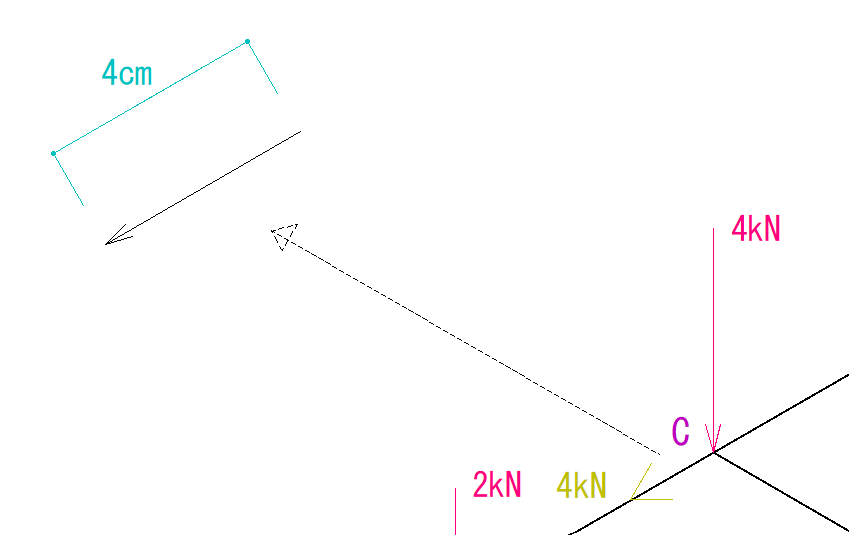
②C点示力図を描いて解く
同じようにC点もやっていきます。
このC点は、すでに2か所力の大きさが分かっているので、分かっている場所から時計回りに移動させていきます。

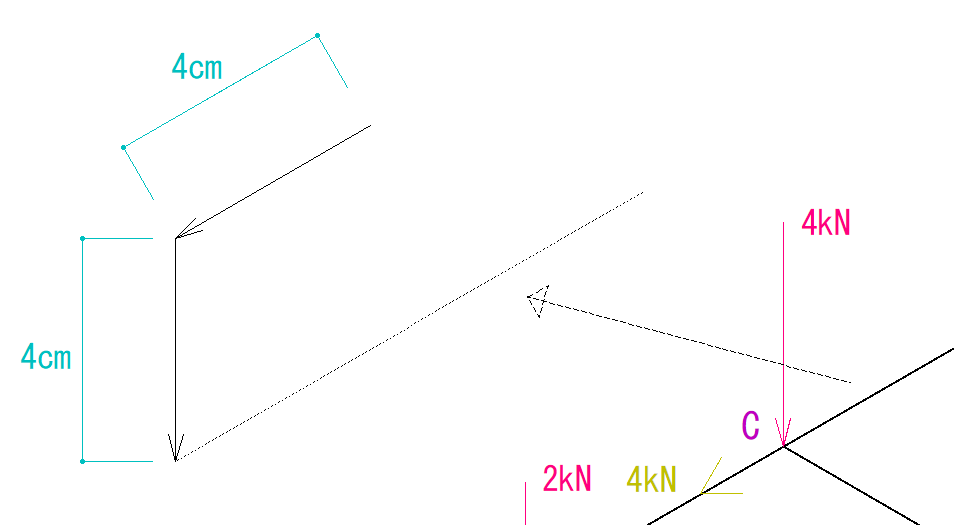
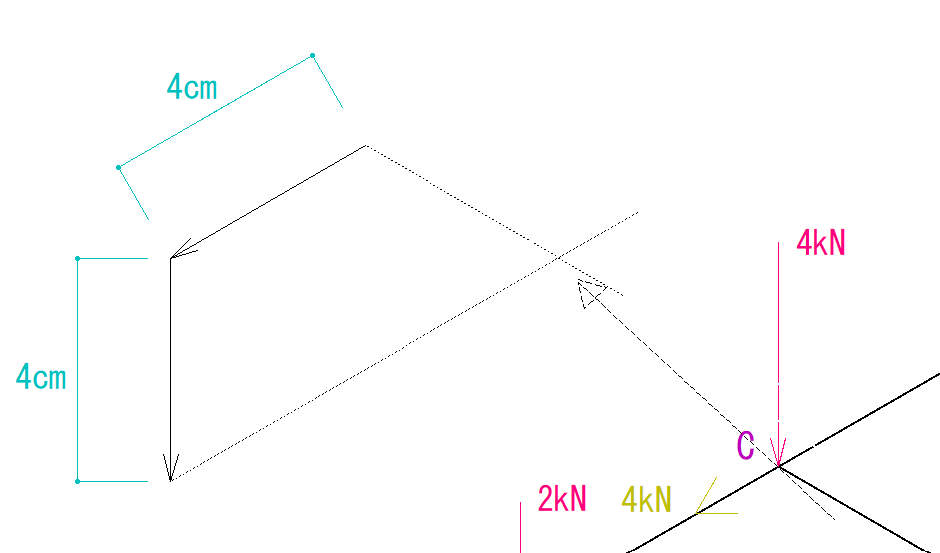
最終的に示力図が閉じる形になるようにします。
ここまできたら先程と同じです。
矢印の向きがが一周するように付け、それぞれの辺の長さ定規ではかります。

最後に軸方向力の向きと大きさをそれぞれ答えに書き込んで終了です。
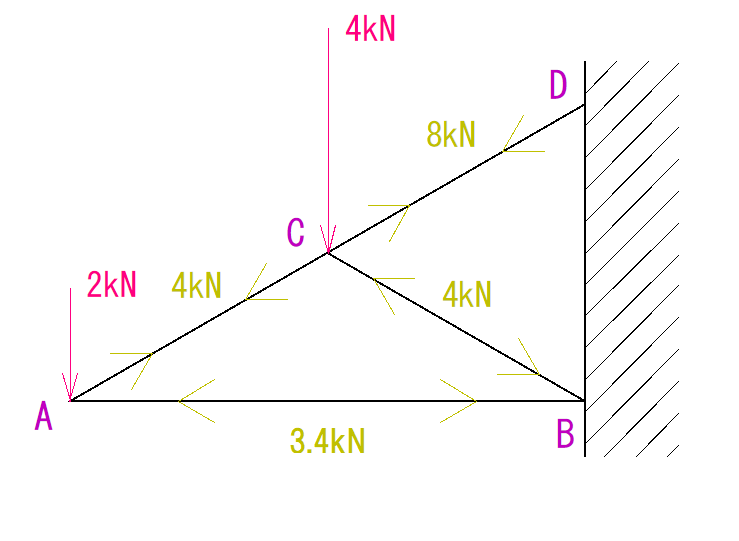
今回は少なかったですが、トラスがいっぱいあっても、一つずつやっていくと解けていきます。
まとめ
この「節点法」の図式解法ですが、実はあまり使いません。
正確に写して、正確に測る必要があり、誤差が生じやすいからです。
また、一つ一つ考えるやり方とは別に「クレモナの図式解法」という解き方もありますが、誤差が生じやすいのは変わりません。
テストや試験にもそこまで重要視されて出題はされないと思います。
(あくまで個人的な感想です)
「クレモナの図式解法」については、また別の記事で解説したいと思います。