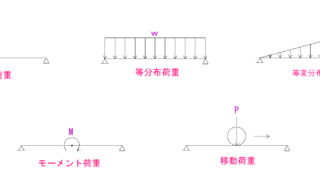
今回は片持梁に等分布荷重がかかった場合のQ(せん断力)図M(曲げモーメント)図の描き方を解説していきたいと思います。
先回は集中荷重の解説をしましたが、そちらで片持梁の解き方も解説しました。
今回も同じような考え方をするので、まだ見ておられない方は下のリンクからご覧ください。
では早速、等分布荷重がかかったときの解説を行っていきたいと思います。
例題
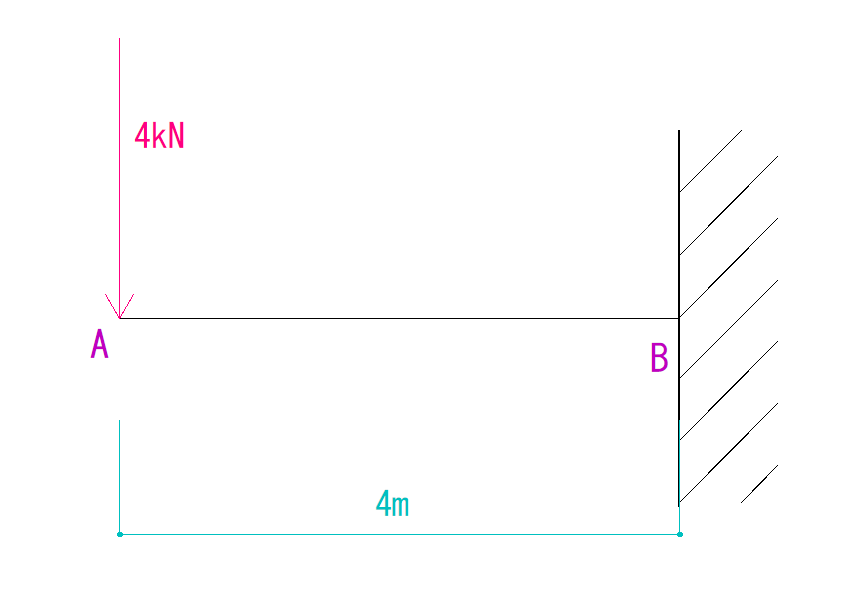
下の図を見てQ図M図を求めなさい。
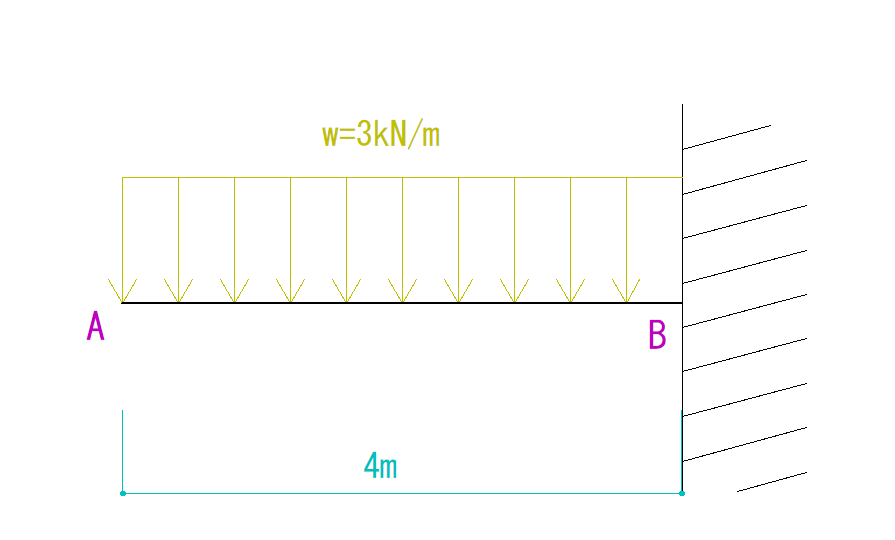
解説
反力の仮定
まずは反力の仮定を行っていきます。
先回も確認しましたが、片持梁の場合、反力が出るのは片方の支点だけです。
片持梁の支点や反力数については下のリンクの記事をご覧ください。
そこから、下のような反力が生じることが分かります。
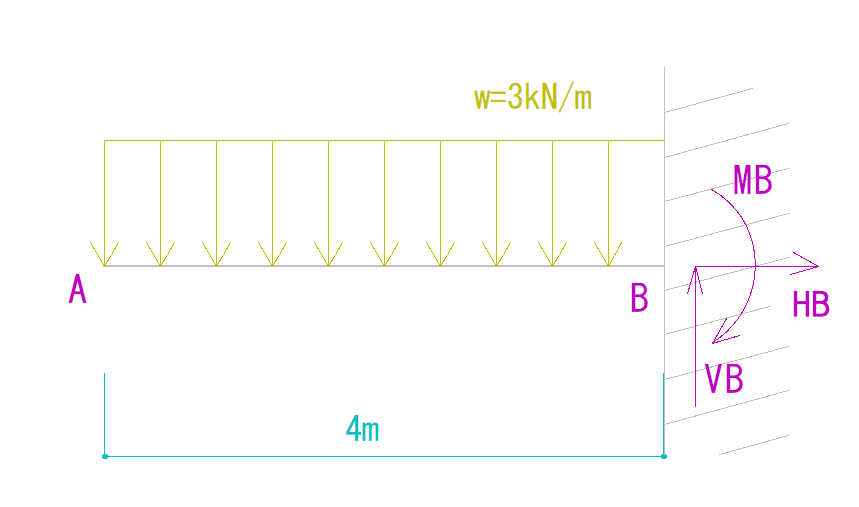
では、これらを一つ一つ考えていきます。
(水平反力は今回生じないので割愛します。)
しかしその前に、等分布荷重が何かというのを理解する必要があります。
そちらを先に解説したいと思います。
復習しておきたいという方は下のリンクの記事をご覧ください。
等分布荷重の解き方
等分布荷重のままだと計算がしづらいため、最初に対応する合力を求めます。
等分布荷重の合力は
等分布荷重がかかっているところの距離[l]×等分布荷重の厚さ[w]
でした。
なので今回は、
等分布荷重がかかっているところの距離[l] = 4m
等分布荷重の厚さ[w] = 3kN/m
より、
4 × 3 = 12kN
となります。
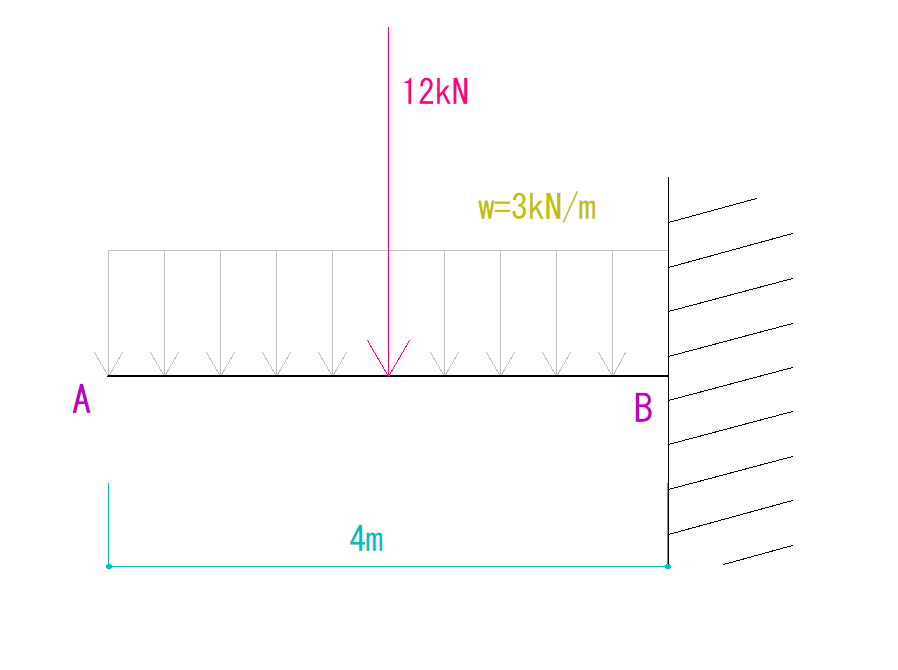
合力がかかっているのは、重心の場所
つまり、A点から右に2mの場所だとわかります。
(詳しくは先程のリンクの記事をご覧ください。)
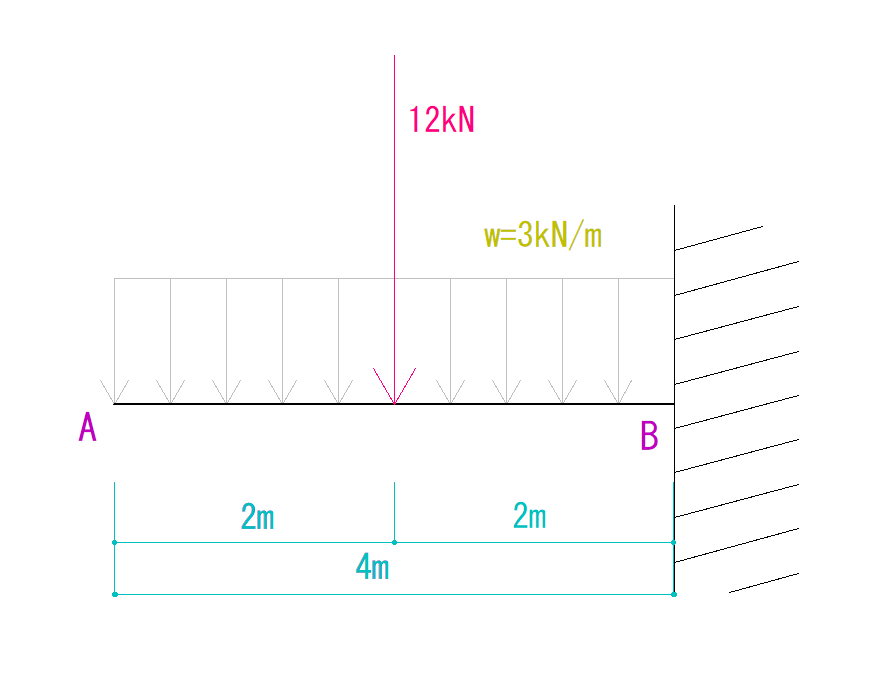
これでようやく反力を求められます。
早速考えていきましょう。
垂直力(せん断力)
これは簡単ですね。
上から下に12kNで力がかかっているので、VBは下から上に12kNの力がかかる必要があります。
式で書くなら下の通りです。
ΣY=0より、
R+VB=0
-12kN + VB = 0
VB = 12kN
となります。
(なぜRの12kNにマイナスが付いているかというと、下向きの荷重だからです。)
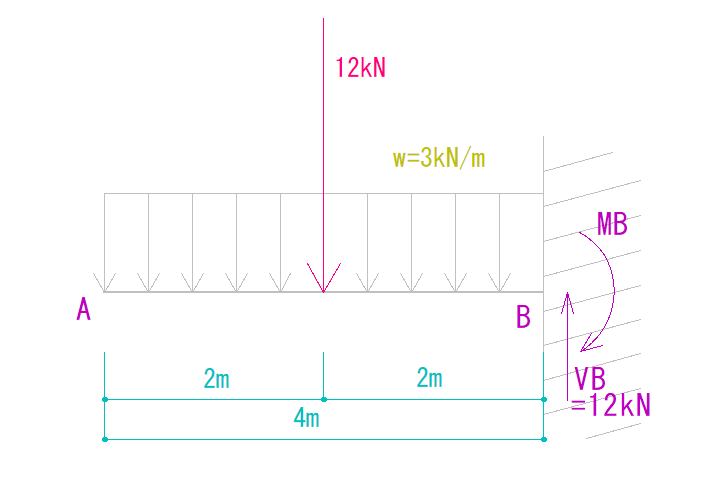
モーメント力
まずは荷重がB点を回す力を求めましょう。
モーメント力について復習したい方は下のリンクの記事をご覧ください。
モーメント力の公式より
12kN × 2m = 24kN・m
反時計回りの為、負の符号をつけて
-24kN・m
となります。
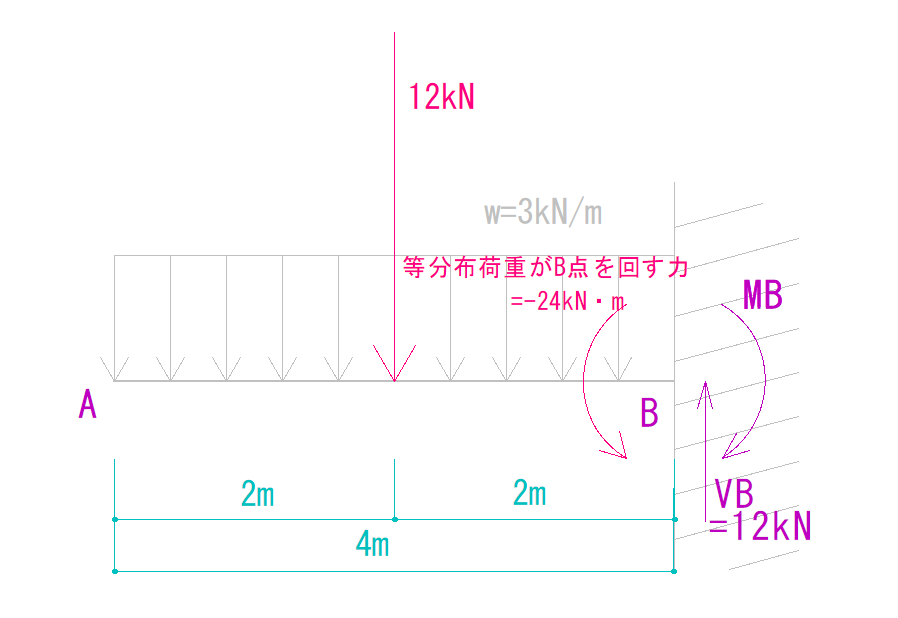
そこから反力を求めると、
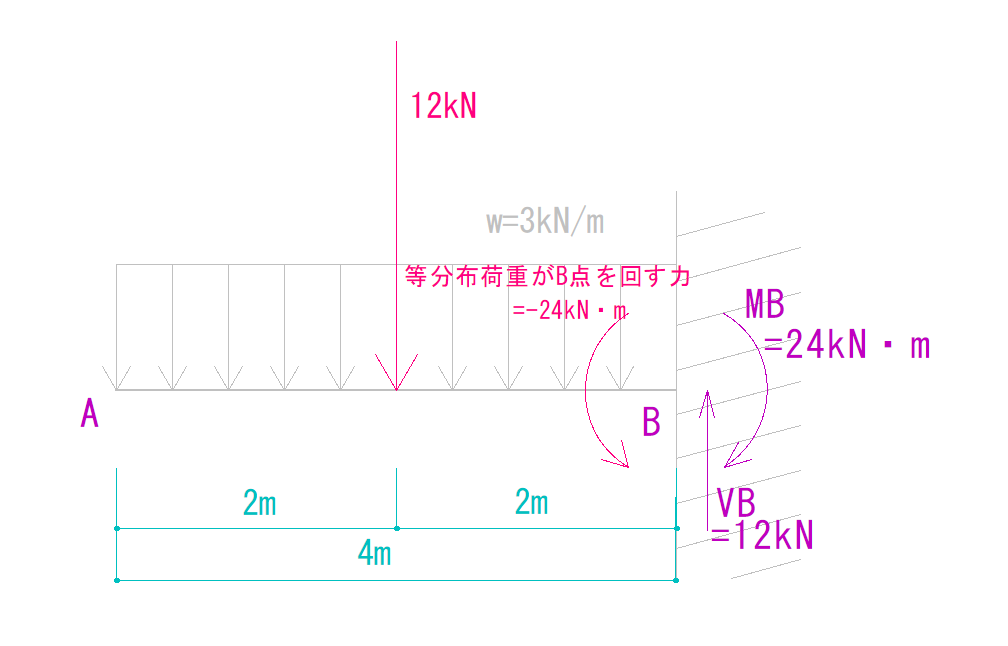
ΣMB=0より
-24kN・m + MB = 0
MB = 24kN・m(仮定通り時計回り)
となります。
Q図の描き方
描き方は単純梁&等分布荷重の時と同様です。
その時の記事で詳しく解説してありますので、今回はさらっと行きたいと思います。
詳しく見たい方は下のリンクの記事をご覧ください。
まず、前提として等分布荷重のQ図は直線形(三角形型)になります。
つまり、等分布荷重の端と端が分かればあとは直線で結ぶだけ、ということです。
それでは問題を見てみましょう。
今回も左から(右からでも可)見ていきたいと思います。
A点ですが、支点がないので垂直力も生じていません。
つまり、0ということです。

次にB点を見てみます。
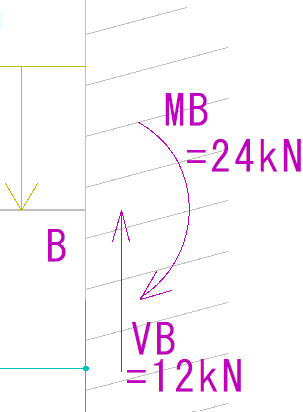
ここでは垂直力がしっかりとかかっていますね。
部材の右側が上方向にせん断されています。
この場合、符号は+と-どちらになるでしょうか?
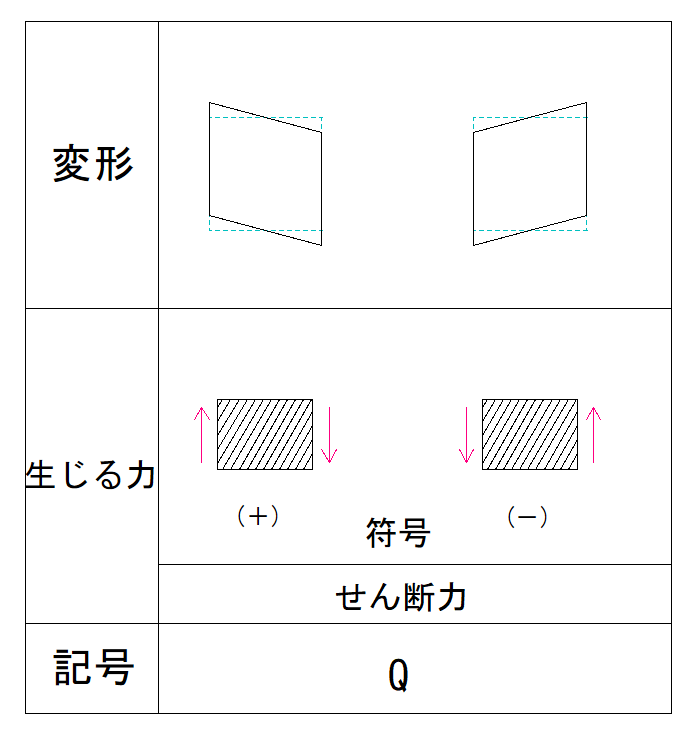
上の表を見るとわかる通り、今回の問題はマイナスです。
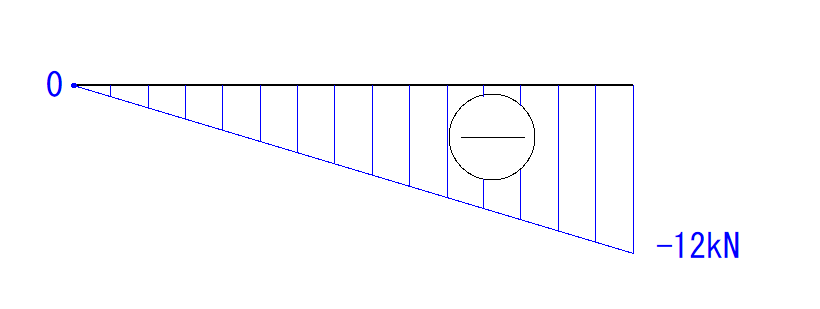
大きさはVBのまま、12kNとなります。

あとは直線で結び、大きさと符号を書き入れれば完成です。
M図の描き方
こちらは、単純梁&等分布荷重の時と少し違う形になります。
ただ基本は同じです。
それは
等分布荷重のM図は2次曲線になる
ということです。
しかも片持梁の場合2次曲線の半分だけの形になります。
言葉ではうまく伝わらないと思うので例題を解いていきましょう。
まず、いつものように左から(右からでも可)見ていきたいと思います。
A点には支点がないのでM値も0になります。

B点はどうでしょうか?
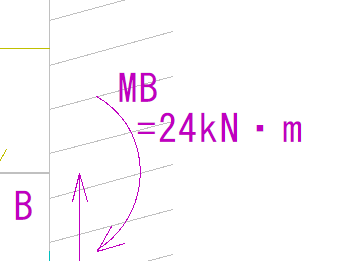
MBがかかっているのでM値はその値のまんま、24kN・mとなります。
符号を確認しましょう。
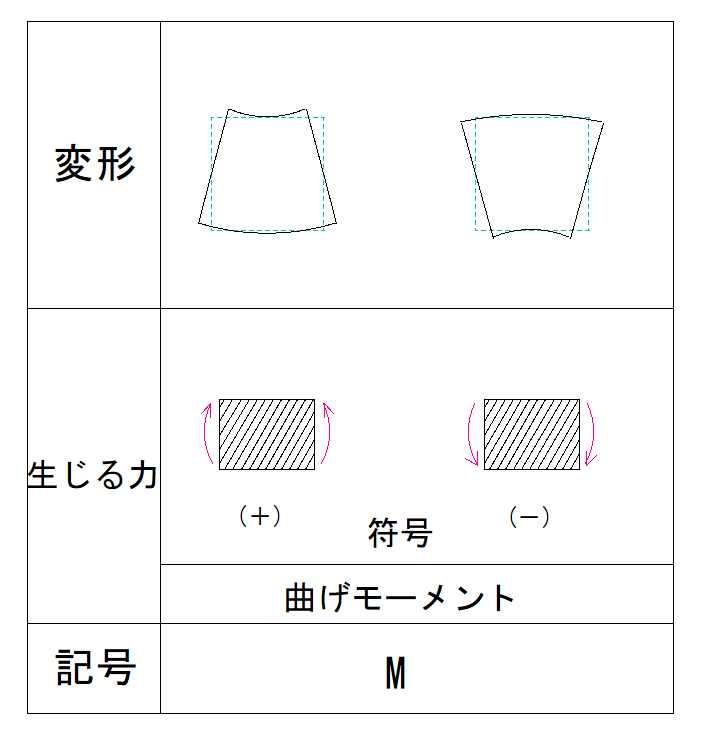
上の表を見ると符号はマイナスだということが分かります。
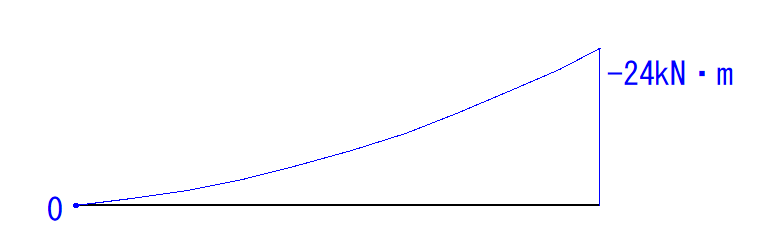
なので、B点のM値は-24kN・mということが分かります。

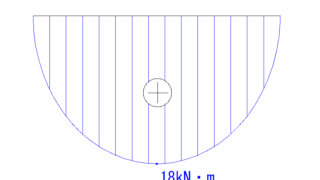
そうしたら、あとはこの2点を2次曲線でつなぎます。
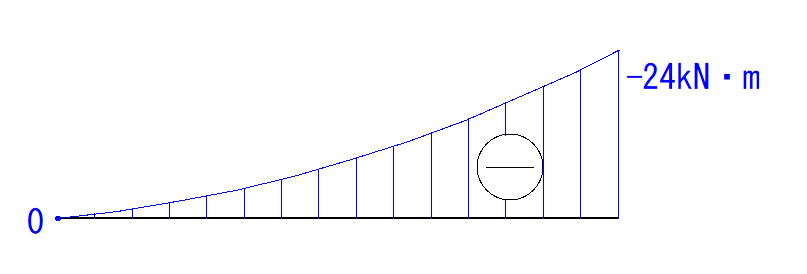
注意
下のようにならないよう気を付けてください。
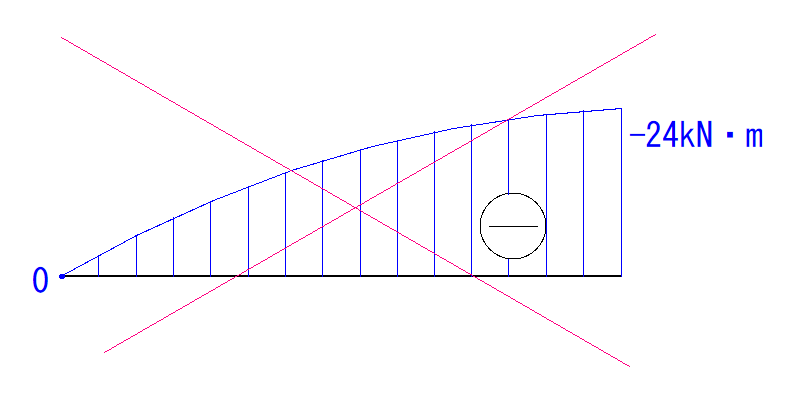
確かにこれも2次曲線ですが、片持梁の場合、支点がない方向から徐々に増加率が高くなっていきます。
しっかりと理解しておきましょう。