今回は重ね合わせの原理について解説していきたいと思います。
先回までの記事で一通り単純梁にかかる荷重のQ図M図の描き方を解説してきました。
まだご覧になっていない方は下のリンクからご覧ください。
重ね合わせの原理、と聞いてもあまりピンとこないかもしれません。
まずは単語の意味から解説していきたいと思います。
「重ね合わせの原理」とは?
まずはWikipedia先生の解説を見てみましょう。
物理学およびシステム理論における重ね合わせの原理[1](かさねあわせのげんり、英: superposition principle[2])とは、線形な系一般に成り立つ徴的な原理。二つ以上の入力が同時に与えられた時に系が返す応答が、それぞれの入力が単独に加えられた場合に返される応答の総和となることをいう。つまり、入力 A に対して応答 X が返され、入力 B に対して応答 Y が返されるならば、入力 ( A + B ) に対して返される応答は ( X + Y ) である。
Wikipedia 「重ね合わせの原理」
…さて、これらを簡単に解説したいと思います。
「重ね合わせの原理」とは簡単に言うと、二つの力が加わると、合わさった力はその二つの力の和になりますよ、という原理です。
例えで考えてみましょう。
池に石を落とすと波が出ますよね。

それを少し離れた場所で2個同時に落としてみます。
そうすると二つの石を中心に波ができて、
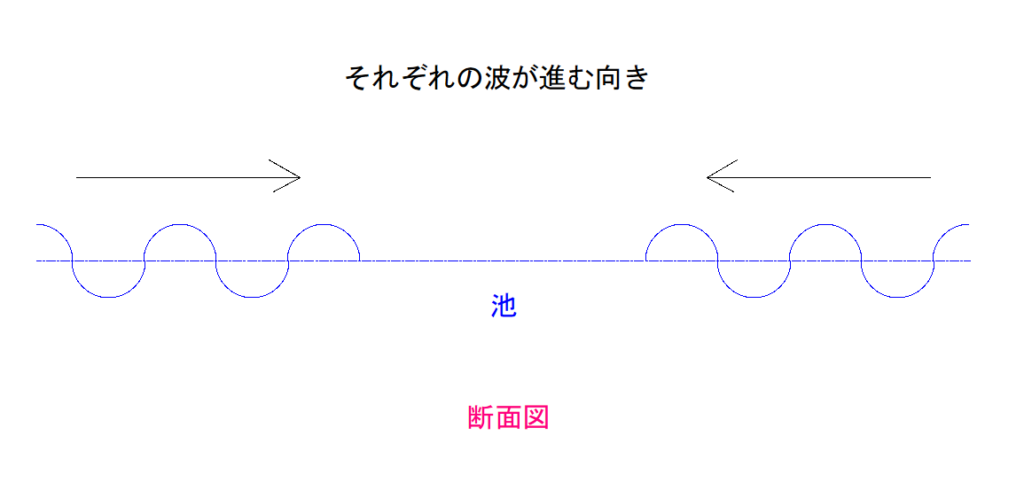
そのうち波同士がぶつかります。
その時、波の高いところ同士でぶつかれば、ぶつかった瞬間波は高くなります。
どれぐらい高くなるかというと、2つの波の高さの和の分高くなります。
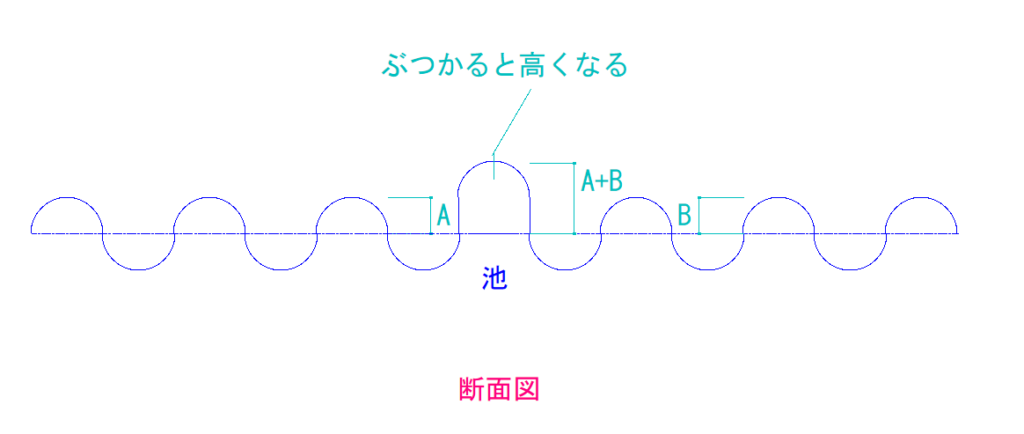
これが重ね合わせの原理です。
そんなに難しいことではないのですが、とりあえず、
「2つの波がぶつかったときはその場所の和を求めればいいんだなぁ」
と考えてください。
N図Q図M図の重ね合わせの原理とは
さて、「重ね合わせの原理」についてなんとなく理解したところで、本題に入っていきたいと思います。
N図Q図M図では、重ね合わせの原理をいつ使うのでしょうか?
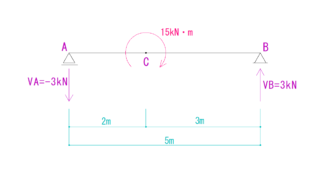
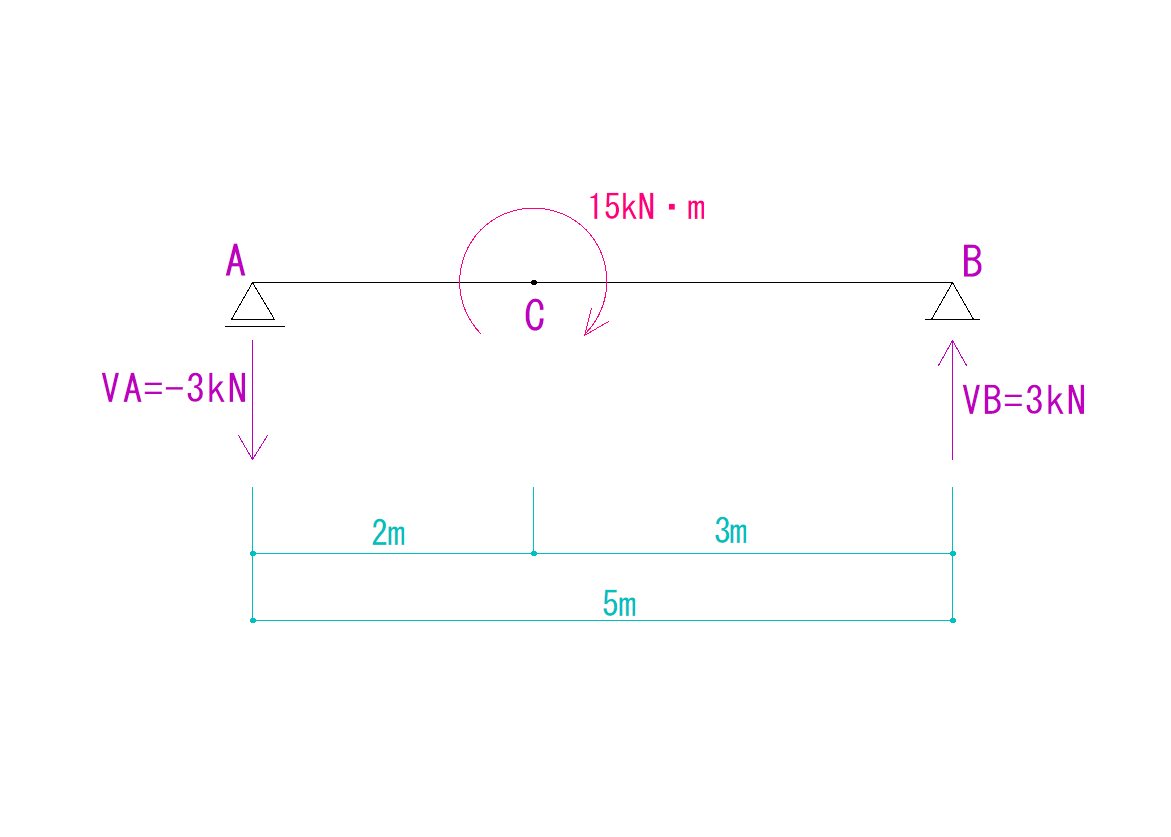
下の例題を見てください。
例題
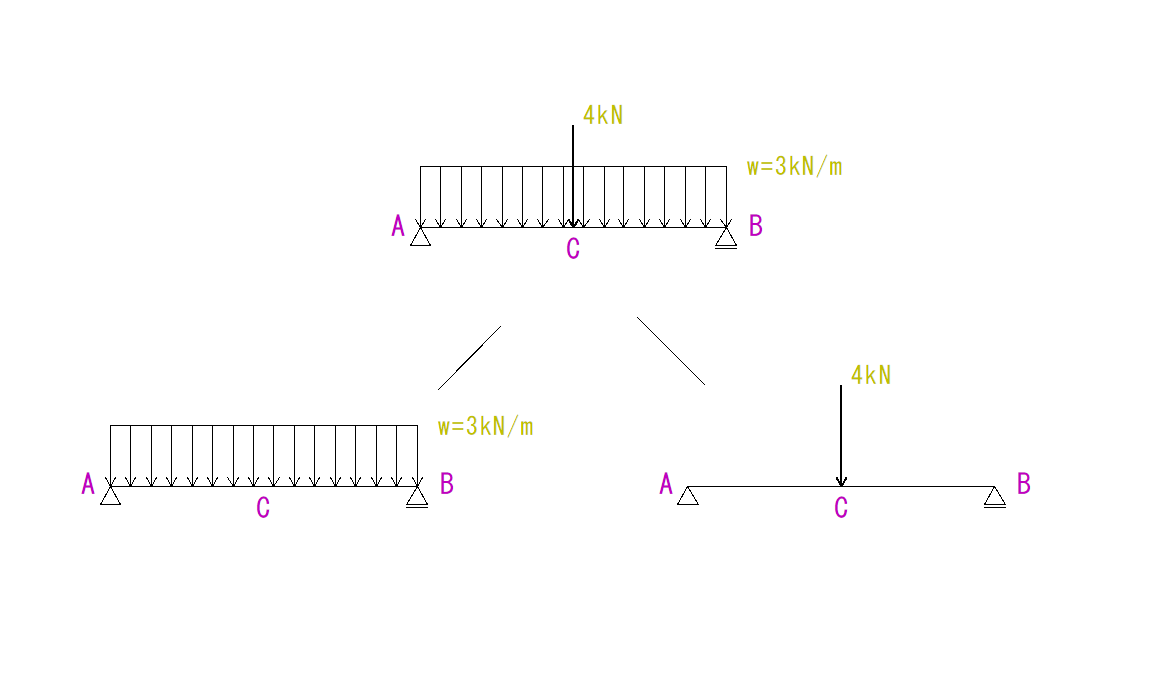
下の図を見てQ図M図を求めなさい。
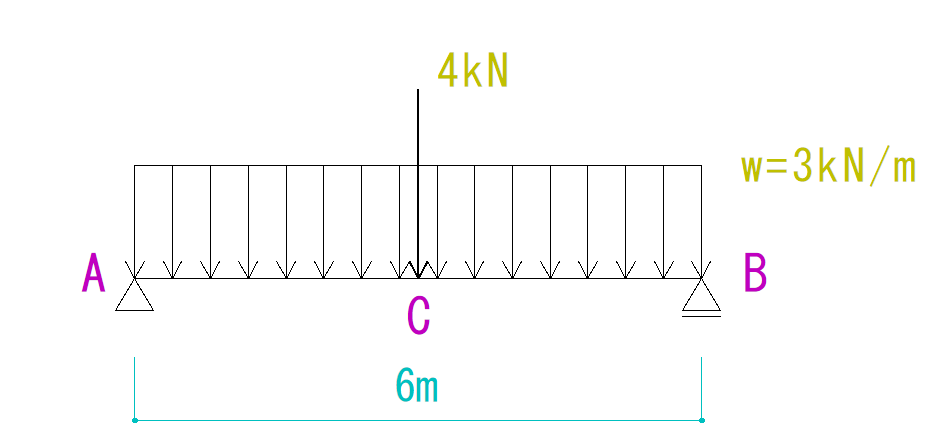
これは少し応用編です。
集中荷重と等分布荷重が二つ重なっています。
このような時に重ね合わせの原理を使います!
では、解説していきます。
解説
手順1 分解してQ図M図を求める
最初から一気に計算はしていきません。
まずは分解して一つずつ考えます。
これは集中荷重と等分布荷重が組み合わさっている問題なので、それぞれに分けます。
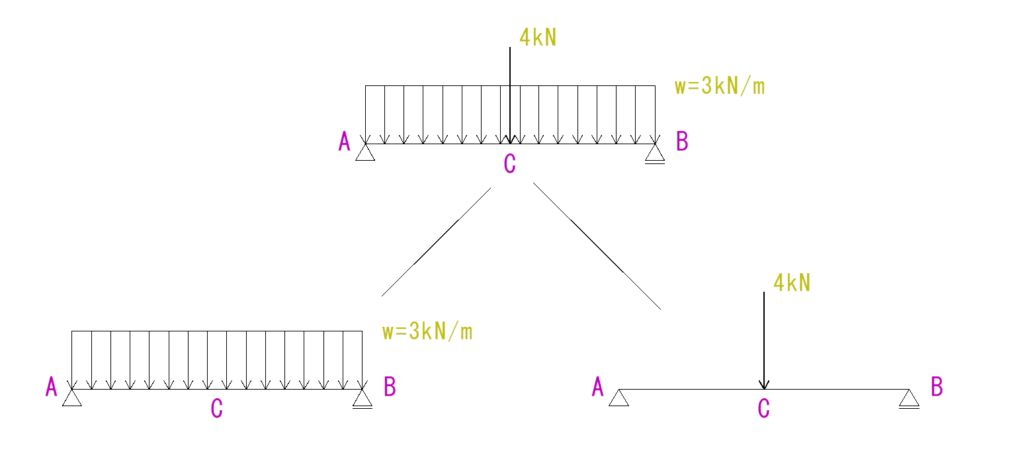
そして、それぞれの反力を求めてから、Q図M図を求めていきます。
それぞれのやり方は下の記事を見てください。
…色々やると、下のような結果になると思います。
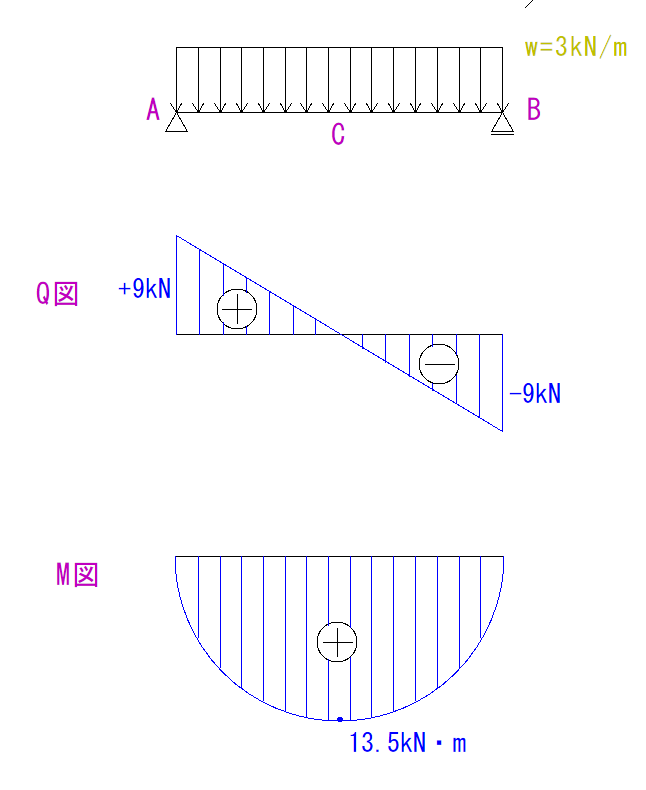

そうしたら手順2です。
手順2 Q図M図を重ね合わせる
ここで「重ね合わせの原理」が出てきます。
ただやることは簡単です。
それぞれの値を足すだけだからです。
一つずつ考えましょう。
先程の例えでは、波がぶつかった瞬間の話をしましたが、今回は図すべてが重なります。
つまり、
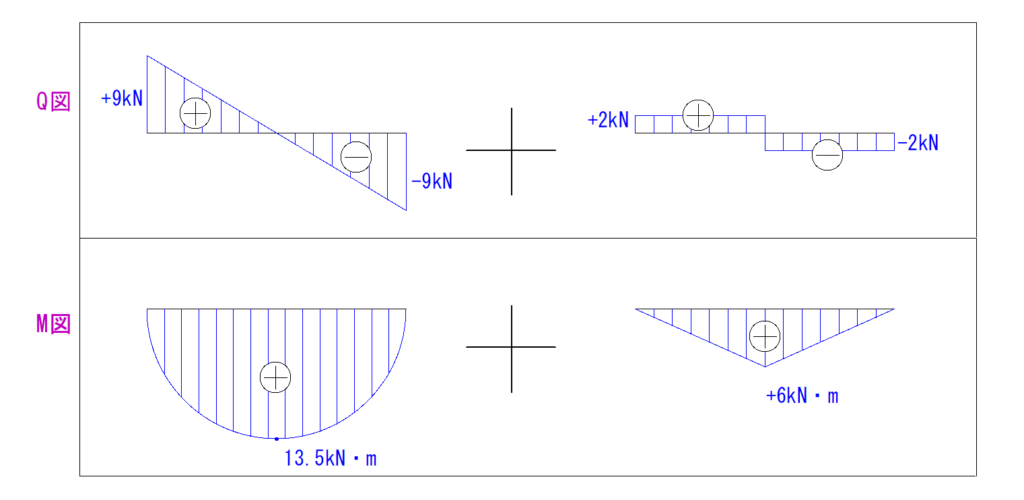
…ということです。
まずはQ図から考えましょう。
Q図の重ね方
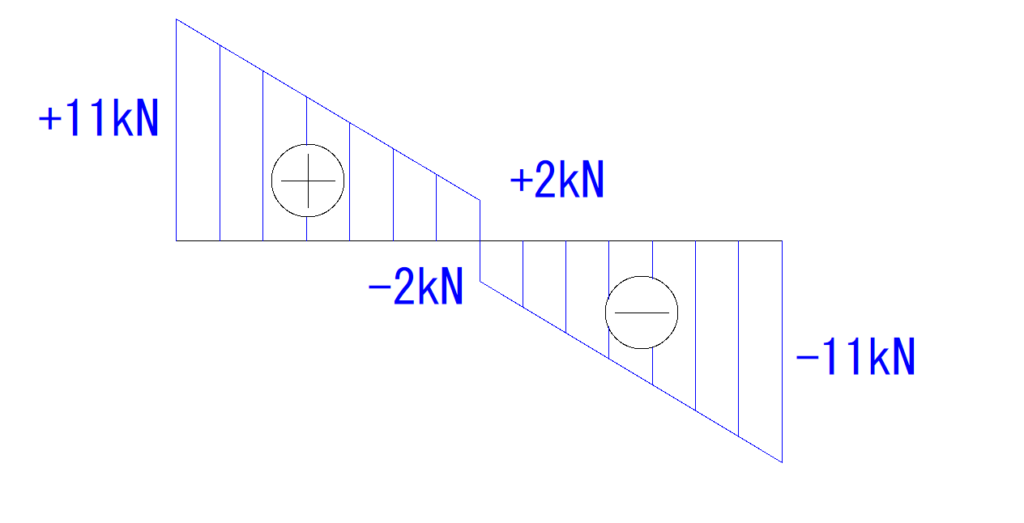
図を左から(右からでも可)見ていきます。
最初はA点です。
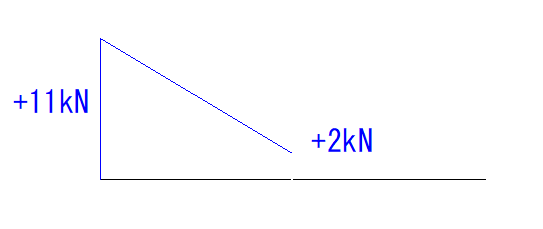
等分布荷重のQ図では最初は+9kNとなっています。
集中荷重の方は+2kNです。
なので、それぞれを足して+11kNとなります。

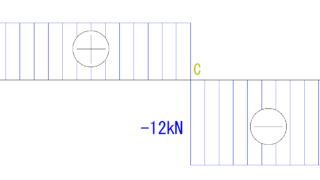
次に荷重がかかっているところはC点です。
C点は、等分布荷重のQ図では最初は0kNとなっています。
集中荷重の方は+2kNです。
それぞれを足して+2kNです。
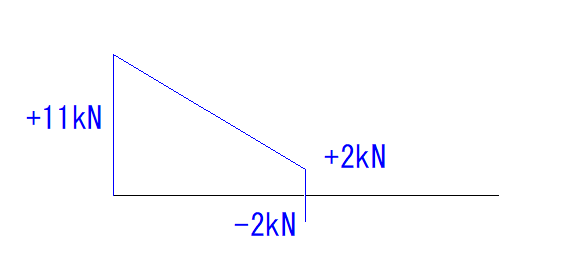
また、集中荷重はC点で-4kN落ちています。
なので、C点のところで同様に-4kN落とします。
最後にB点ですが、等分布荷重のQ図では-9kNとなっています。
集中荷重の方は-2kNです。
なので、それぞれを足して-11kNとなります。
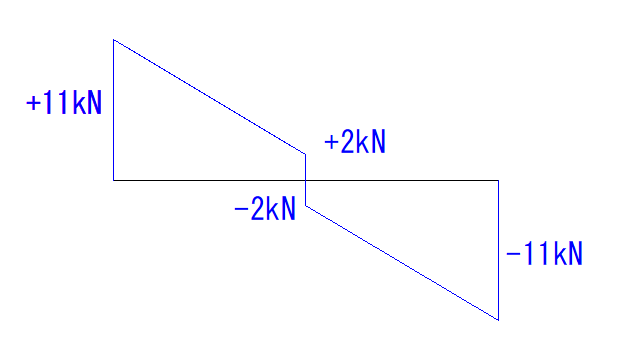
それぞれ図が変わる所ごとに値を入れて、符号を書き入れれば完成です。
M図の重ね方
これはなかなかのクセ者です。
一次関数と二次曲線の組み合わせだからです。
…でも大丈夫!
実はこれ意外と簡単なんです。
なぜなら、
正しい図なんて手書きで書けないから!
つまり、Mmaxの値が分かり、なんとなく直線っぽい2次曲線を描けばいいのです。
それではやってみましょう。
Mmaxを求めます。
求め方はQ図の時と同様です。
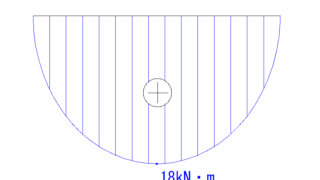
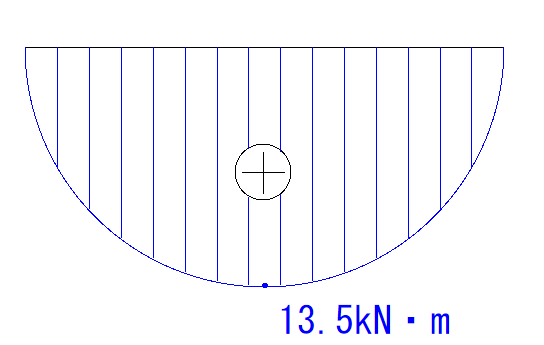
等分布荷重のM図でのMmaxは+13.5kNとなっています。
集中荷重の方は+6kNです。
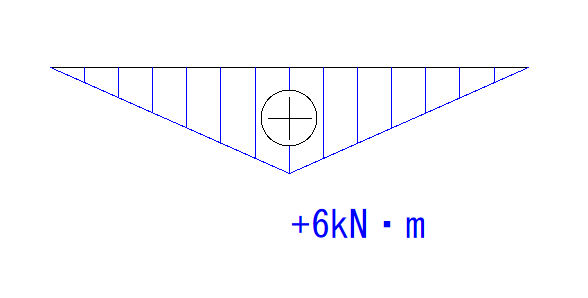
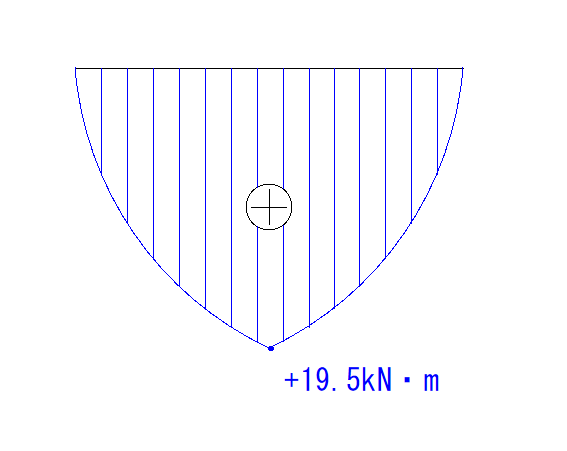
なので、それぞれを足して+19.5kN・mとなります。
あとはいい感じに重ね合わさったような図を描き完成です。